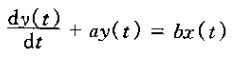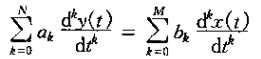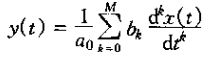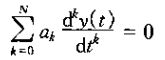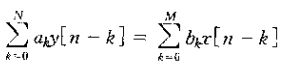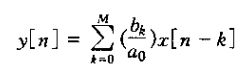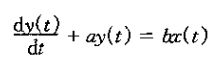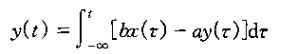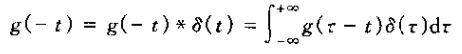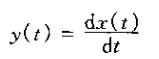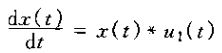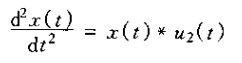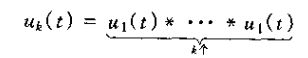《信号与系统学习笔记》—线性时不变系统(二)
注:本博客是基于奥本海姆《信号与系统》第二版编写,主要是为了自己学习的复习与加深。
一、用微分和差分方程描述的因果线性时不变系统
1、一类极为重要的连续时间系统是其输入输出关系用线性常系数微分方程描述的系统。这种形式的方程可以用来描述范围官广泛的系统和屋里现象。
2、一类极为重要的离散时间系统是其输入输出关系用线性常系数差分方程描述的系统。这种形式的方程可以用来描述许多不同过程的程序行为。
一)、线性常系数微分方程
1、考虑一阶微分方程:
其中y(t)为系统的输出,x(t)为系统的输入。这类方程所给出的是该系统的一种隐含的特性,也就是说,它们所描述的输入和输出关系并不是将系统输出作为输入函数的一种明确的表达式。
2、一般来说,为了求解一个微分方程,必须给定一个或多个附加条件;一旦这些条件给定,原则上就能得到一个用输入表示输出的明确的表达式。
3、一个N阶线性常系数微分方程由如下方程给出:
阶次指的是出现在这个方程输出y(t)的最高阶导数。当N=O时,上式就变为
此时y(t)就是输入x(t)及其导数的一个明确的函数。
4、N阶线性常系数微分方程的阶由两部分组成:特解加上如下齐次微分方程的解
此方程称为该系统的自然响应。
二)、线性常系数差分方程
1、离散时间N阶线性常系数差分方程
上式可以用求解微分方程那样来求解。具体而言,y[n]的解可以写成特解和一个齐次方程
2、N阶线性常系数差分方程另一种表达式为
上式可把n时刻的输出直接用以前输入输出值来表示;据此可立即看出需要附加条件。为了计算y[n],就需要知道y[n-1],...,y[n-n],因此如果给出了所有n时的输入和一组附加条件,就可以连续求得个y[n]的值。两种N阶线性常系数差分方程称之为递归方程。
3、在N=0的特殊情况下,上式就变成
此方程称为非递归方程。由上庙的方程描述了一个线性时不变系统,这个系统的单位脉冲响应为
此系统往往称为有限脉冲响应系统。
三)、用微分和差分方程描述的一阶系统的方框图表示
1、由线性常系数差分方程和微分方程描述的系统的一个重要特点是:能以很简单而且很自然的方式用若干基本运算的方框图互联来表示。这样做很有意义的:
1)、给出一种形象化的表示,这有助于加深对这些系统的特性和性质的理解。
2)、对于系统的仿真和实现有很大的价值。
2、离散时间三种基本的网络单元:
3、离散时间一阶差分方程方框图
方框图表示:
4、连续时间三种基本网络单元
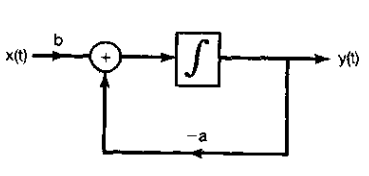
5、连续时间一阶微分方程
1)、不常用微分器
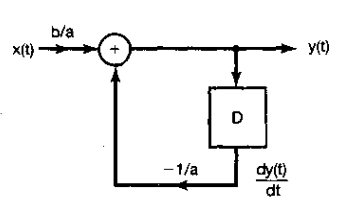
2)、常用微分器
3)、微分器方框图表示:
4)、不常用微分器方框图表示
5)、常用微分器方框图表示
二、奇异函数
一)、作为理想化短脉冲的单位冲激
1、如果将单位冲激定义为某信号的极限形式,那么事实上就存在着无限多个看起来很不同的洗你号,但在极限之下其表现都像一个冲激。这里所指的意思是一个线性时不变系统对所有这些信号的响应应在本质上都是一样的,只要这个脉冲“足够短”,即△"足够小"。
二)、通过卷积定义单位冲激
1、定义一个信号,其对任何x(t)有
由上式可以得到所需的有关单位冲激的全部性质。
1)、若令x(t)=1(对所有的t),则
所以单位冲激的面积为1.
2)、取热门和信号g(t),将其反转得到g(-t),然后再与求卷积。
对于t=0,得
上式说明:单位冲激是这样一种信号,当它与某一信号g(t)相乘并在-∞和+∞积分时,其结果就是g(0)。
三)、单位冲激偶和其他奇异函数
1、单位冲激是一类称为奇异函数的信号中的一种,其中每一种信号都是借助于它在卷积运算中的特性来定义的。
2、考虑输出是输入的导数的线性时不变系统,即
这个系统的单位冲激响应是单位冲激的导数,称为单位冲激偶u1(t)。根据线性时不变系统的卷积表示,对任何信号x(t)应有
可以将上式取为u1(t)的运算定义。同理也能定义二阶导数u2(t),取输入的二阶导数的线性时不变系统的冲激响应为
一般情况下,k>0时,uk(t)就是的k此导数,因此是一个取输入k此导数系统的单位冲激响应。因为该系统可以由k个微积分级联得到,所以就有
3、与单位冲激一样,单位冲激函数等这些奇异函数中的每一个都可以与一些短脉冲相联系。
4、除了单位冲激各不同阶导数的这些奇异函数之外,还能代表单位冲激函数连续多次积分的一些信号。