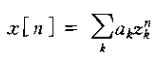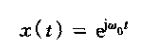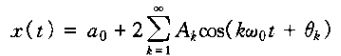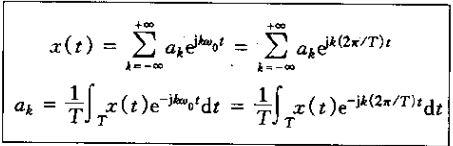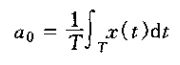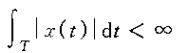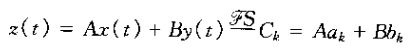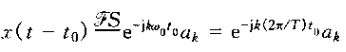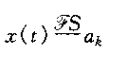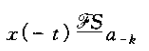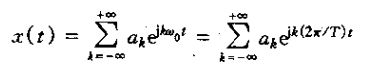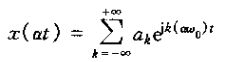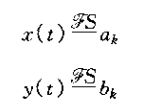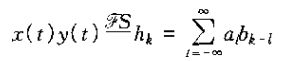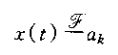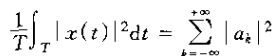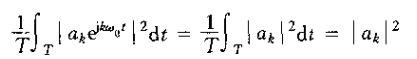《信号与系统学习笔记》—周期信号的博里叶级数表示(一)
注:本博客是基于奥本海姆《信号与系统》第二版编写,主要是为了自己学习的复习与加深。
一、线性时不变系统对复指数信号的响应
1、在研究线性时不变系统时,将信号表示成基本信号的线性组合是很有利的,但这些基本信号应该具有以下两个性质:
1)、有这些基本洗你号能够构成相当广泛的一类有用信号。
2)、线性时不变系统对每一个基本信号的响应都是十分简单的,以使系统对任意输入信号的响应有一个很方便的表达式。
博里叶分析的很多重要价值都来自这一点,即连续和离散时间复数信号集都具有以上两个性质,即连续时间的est和离散时间的zn信号,其中s和z都是复数。
2、在研究线性是不变系统时,复指数洗你号的重要性在于这样一个事实;即一个线性时不变系统对复指数信号的响应也是同样一个复指数信号,不同的只是在幅度上的变化;也就是说:
其中H(s)或H(s)是一个复振幅因子,一般来说是复变量s或a的函数。
3、一个信号,若系统对该信号的输出响应仅是一个常数(可能是复数)乘以输入,则称该信号为系统的特征函数,二振幅因子称为系统的特征值。
4、复指数是连续时间线性时不变系统的特征函数,复指数序列也是离散时间线性时不变系统的特征函数。
5、将信号表示成复指数的线性组合,就会导致一个线性时不变系统响应的方便表达式;
1)、对于连续时间线性时不变系统的输入表示成复指数的线性组合,即
那么输出一定是
2)、对于离散时间线性时不变系统的输入表示成复指数和线性组合,即
那么输出一定是
换句话说,对于连续时间和离散时间来说,如果一个线性时不变系统的输入能够表示成复指数的线性组合,那么系统的·1输出也能够表示成相同复指数信号的线性组合;并且输出表达式中的内一个系数可以用输入中的相应的系数ak分别于特征函数有关的系统特征值H(s)或H(z)相乘来求得。
二、连续时间周期信号的博里叶级数表示
一)、成谐波关系的复指数信号的线性组合
1、周期复指数信号
此信号是周期的,而且基波频率为w0,基波周期T=2π/w0。与上市成谐波关系的复指数信号集就是
这些信号中的每一个都有一个基波频率,他是w0的倍数。因此每一个信号对周期T来说都是周期的。一个有成谐波关系的复指数线性组合形成的信号
对T来说也是周期的。上式的表示称为波例叶级数表示。
2、博里叶级数的另外两种表示
令
则
二)、连续时间周期信号博里叶级数表示的确定
1、博里叶级数的推导
2、如果x(t)有一个博里叶级数表示,即x(t)能表示成一组成谐波关系的复指数信号的线性组合,那么博利叶级数中的系数就可由下式确定
其中分别给出了基博频率w0和基波【inletT表示的博里叶级数的等效表达式。其中一个称之为综合公式,一个称之为分析公式。系数{ak}往往称为x(t)的博里叶级数或称为频谱系数。这些复指数系数对信号x(t)中的每一个分量大小的度量。系数a0就是x(t)中的直流或常数分量,由式以k=0带入可得
这就是x(t)在一个周期内的平均值。
三、博里叶级数的收敛
1、大部分周期性信号不存在任何收敛上的困难。
2、狄里赫利条件;
1)、条件一:在任何周期内,x(t)必须绝对可积,即
与平方可积条件相同。
2)、条件2:在任意区间内,x(t)具有有限个欺负变化;也就是说,在任何单个周期,x(t)的最大值和最小值的数目有限。
3)、在x(t)的任何有限区间内,只有有限个不连续点,而且在这些不连续点上,函数是有限值。
3、对于一个不存在任何间断点的周期信号而言,博里叶级数收敛,并且在没一点上该级数都等于运来的信号x(t)。对于在一个周期内存在有限数目不连续点的周期信号而言,除去那些不连续点外,其余所有店上博里叶级数都等于原来的x(t);而在那些鼓励的不连续点上,博里叶级数收敛于不连续点处的值得平均值。
4、吉伯斯现象
一个不连续信号x(t)的博里叶级数的截断近似xn(t),一般来说,在接近不连续点处将呈现高频起伏和超量。而且,若在实际情况下利用这样一个近似式,就应该选择足够大的N,以保证这些起伏拥有的总能量可以忽略。
四、连续时间博里叶级数性质
假设x(t)是一个周期信号,周期为T,即波频率w0=2π/T。那么,若x(t)的博里叶级数系数记为ak,则用
来表示一个周期信号及其博里叶级数系数的一堆关系。
一)、线性性质
令x(t)和y(t)伪两个周期信号。周期为T,他们的博里叶系数分别为ak和bk,即
x(t)和y(t)的线性组合z(t)=Ax(t)+By(t)的博里叶级数系数ck由x(t)和y(t)的博里叶级数系数的同一线性组合给出,即
二)、时移性质
若
那么
这个性质的一个结果就是:当一个周期信号在时间上移位时,他的博里叶级数系数的模包吃不变,即时|ak|=|bk|。
三)|时间反转
若
那么
换句话说,施加于连续时间洗你号上的时间反转会导致其对应的博里叶级数系数序列的时间反转。时间反转的一种结果是:若x(t)为偶函数,则其博里叶级数系数叶为偶,即a-k=ak,若为奇函数,则其博里叶级数系数也为奇,即a-k=-ak。
四)、时域尺度变换
若x(t)具有下式的表示
那么
就是x(at)的玻璃也级数表示。要强调的事,虽然博里叶系数没有改变,但由于基波频率变化了,波例叶级数表示缺改变了。
五)、相乘
若
那么
六)、共轭及共轭对称
将一个周期信号x(t)取它的复数共轭,在它的博里叶级数系数上就会有复数共轭并进行时间反转的结果,即若
那么
由上式可以看出,由于x(t)=x*(t),博里叶级数系数就一定是共轭对称的,即
七)、连续时间周期信号的帕斯瓦尔定理
连续时间周期信号的帕斯瓦尔定理是
其中ak是x(t)的博里叶系数,T是该信号的周期。上式在一个周期内的平均功率(也就是单位时间内的能量),而同时有
所以|ak|2就是x(t)中第k次谐波的平均功率。于是,帕斯瓦尔定理所说的是:一个周期信号的总平均功率等于它的全部谐波分量的平均功率之和。
八)、连续时间博里叶级数性质列表