(洛谷) P2763 试题库问题（网络流dinic+建图）

题目描述

«问题描述：

假设一个试题库中有n道试题。每道试题都标明了所属类别。同一道题可能有多个类别属性。现要从题库中抽取m 道题组成试卷。并要求试卷包含指定类型的试题。试设计一个满足要求的组卷算法。

«编程任务：

对于给定的组卷要求，计算满足要求的组卷方案。

输入输出格式

输入格式：
第1行有2个正整数k和n (2 <=k<= 20, k<=n<= 1000)

k 表示题库中试题类型总数，n 表示题库中试题总数。第2 行有k 个正整数，第i 个正整数表示要选出的类型i的题数。这k个数相加就是要选出的总题数m。接下来的n行给出了题库中每个试题的类型信息。每行的第1 个正整数p表明该题可以属于p类，接着的p个数是该题所属的类型号。

输出格式：
第i 行输出 “i：”后接类型i的题号。如果有多个满足要求的方案，只要输出1个方案。如果问题无解，则输出“No Solution!”。

输入输出样例

输入样例#1： 复制
3 15
3 3 4
2 1 2
1 3
1 3
1 3
1 3
3 1 2 3
2 2 3
2 1 3
1 2
1 2
2 1 2
2 1 3
2 1 2
1 1
3 1 2 3
输出样例#1： 复制
1: 1 6 8
2: 7 9 10
3: 2 3 4 5

建图：
这题一看就是网络流问题，然后就是怎么建图~
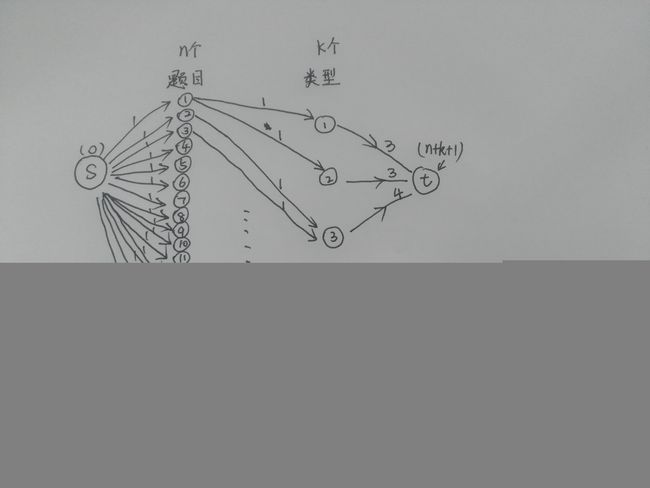
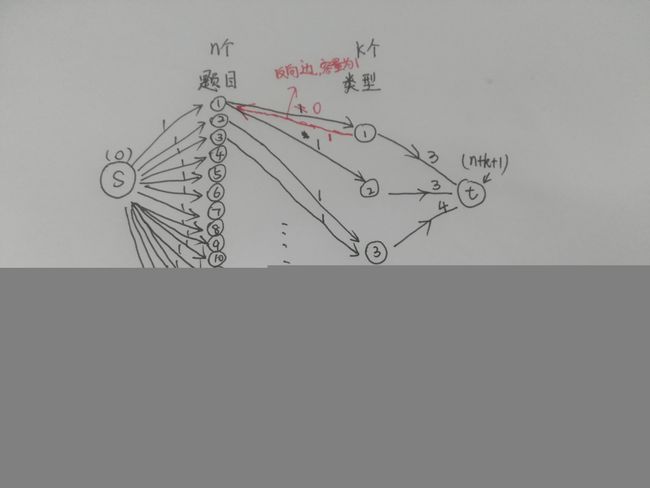
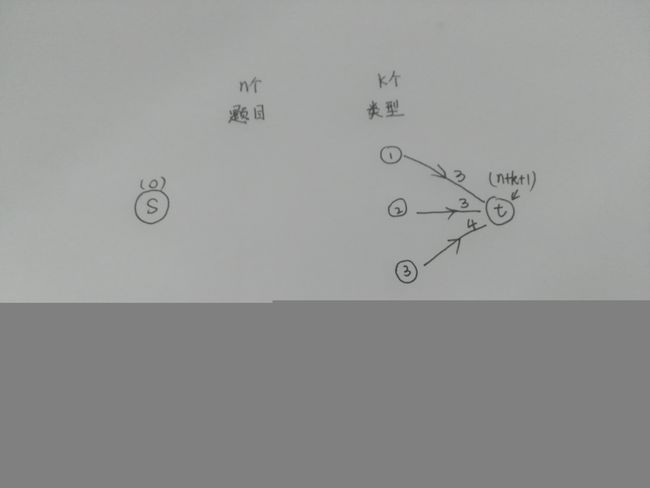
首先，我们自己选择两个点（一个源点：0， 一个汇点：k+n+1(下面再讲为什么)），然后对于源点（0）来说，要和每一道题目建立一条容量为1的边；对于每一种类型来说，都要与汇点（n+k+1）建立一条容量为所要选择此类型的题目数量的边；对于每一道题目来说，都要与这道题目所属类型建立一条容量为1的边。如此，图就建好了。（所有反向边我都没说，但是要建立）
如下图，建边

如下图，继续建边

如下图，寻找第i个类型，用到了哪几个题目

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define INF 0x3f3f3f3f
using namespace std;
#define MAX 1400
struct edge
{
    int to, cap, rev;
    //终点，容量，反向边
};
vectorG[MAX];//二维
int level[MAX];//bfs，对于每个节点来说给出一个层次，分层图
int iter[MAX];//优化，当前弧，在其之前的边已经没有用了
int a[1234], cost;//  对于第i种类型，要选择a[i]个题目  要选择的总题目数（a数组加和）
void add_edge(int from, int to, int cap)//建边
{
    struct edge a;
    a.to=to;
    a.cap = cap;
    a.rev = G[to].size();
    G[from].push_back(a);
    a.to = from;
    a.cap = 0;
    a.rev = G[from].size()-1;
    G[to].push_back(a);
}
void bfs(int s)
{
    memset(level, -1, sizeof(level));
    queue<int>q;
    level[s] = 0;
    q.push(s);
    while(!q.empty())
    {
        int v = q.front();
        q.pop();
        for(int i=0; iif(level[e.to]<0&&e.cap>0)
            {
                level[e.to] = level[v]+1;
                q.push(e.to);
            }
        }
    }
}
int dfs(int v, int t, int f)
{
    if(v==t)
        return f;
    for(int &i=iter[v]; iif(level[e.to]>level[v]&&e.cap>0)
        {
            int d = dfs(e.to, t, min(f, e.cap));
            if(d>0)
            {
                e.cap -= d;
                G[e.to][e.rev].cap += d;
                return d;
            }
        }
    }
    return 0;
}
int max_flow(int s, int t)
{
    int flow = 0;
    for(;;)
    {
        bfs(s);
        if(level[t]<0)
            return flow;
        memset(iter, 0, sizeof(iter));
        int f;
        while((f=dfs(s, t, INF))>0)
        {
            flow += f;
            if(flow==cost)//每增加一道题目，就会减少1，所以只要判断流量==需要的题目数就找到了
                return flow;
        }
    }
}
int main()
{
    int k, n;
    scanf("%d %d", &k, &n);
    //k:类型    n:题数
    for(int i=0; i2; i++)
    {
        G[i].clear();
    }
    for(int i=1; i<=k; i++)//每种类型所需要的题目数
    {
        scanf("%d", &a[i]);
        cost += a[i];//需要的总题目数
        add_edge(i+n, k+n+1, a[i]);//从类型到汇点，增加边容量为a[i]
    }
    for(int i=1; i<=n; i++)//对于每道题目
    {
        int p;
        scanf("%d", &p);//属于几个类型
        add_edge(0, i, 1);
        for(int kk=1; kk<=p; kk++)//分别是哪几个
        {
            int u;
            scanf("%d", &u);
            add_edge(i, u+n, 1);//建边
        }
    }
    int f = max_flow(0, n+k+1);//dinic 找流
    if(f!=cost)//只要不是和总题目数一样，就没有答案
    {
        printf("No Solution!\n");
    }
    else
    {
        for(int i=1;i<=k;i++)//每一种类型
        {
            printf("%d:", i);
            for(int j=0;j//观察他们的反向边，如果流量为1就说明这道题目符合
            {
                edge & e = G[n+i][j];
                if(e.cap==1)
                {
                    printf(" %d", e.to);
                }
            }
            printf("\n");
        }
    }
    return 0;
}