AOJ 894 (无向图的回溯着色法,四色)
Description
花老师有一个农场,农场的花一共有 4 种颜色, 花老师不喜欢老旧的东西,所以,她希望每天种花的方案都不一样。特别地,她也觉得两种一样颜色的花种在相邻的位置会很无聊。现在,她想知道,一共有多少种花的方案。这里要注意的是,农场的种花的位置是不规则的。因此我们给出一对一对的相邻的位置的关系。
Input
第一行两个数 N 和 M,表示种花的位置的个数和相邻的位置的对数
接下来 M 行,每行一组数 A, B 表示 A, B 相邻
接下来 M 行,每行一组数 A, B 表示 A, B 相邻
Output
一个数表示染色方法数
Sample Input
5 4 1 2 1 3 1 4 1 5
Sample Output
324
Hint
N<=10,M<=50
问题背景
给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色,每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点(即相邻顶点)着不同颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色,则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。
输入:无向图,m
输出:如果能,则输出方案
四色问题是m图着色问题的一个特例,根据四色原理,证明平面或球面上的任何地图的所有区域都至多可用四种颜色来着色,并使任何两个有一段公共边界的相邻区域没有相同的颜色。这个问题可转换成对一平面图的4着色判定问题(平面图是一个能画于平面上而边无任何交叉的图)。
将地图的每个区域变成一个结点,若两个区域相邻,则相应的结点用一条边连接起来。多年来,虽然已证明用5种颜色足以对任一幅地图着色,但是一直找不到一定要求多于4种颜色的地图。直到1976年这个问题才由爱普尔,黑肯和考西利用电子计算机的帮助得以解决。他们证明了4种颜色足以对任何地图着色。
回溯法
可以通过回溯的方法,不断的为每一个节点着色,在前面n-1个节点都合法的着色之后,开始对第n个节点进行着色,这时候枚举可用的m个颜色,通过和第n个节点相邻的节点的颜色,来判断这个颜色是否合法,如果找到那么一种颜色使得第n个节点能够着色,那么说明m种颜色的方案是可行的。
步骤:
首先把所有顶点的颜色初始化为0,然后依次为每个顶点着色。在图着色问题的解空间树中,如果从根节点到当前节点对应一个部分解,也就是目前所有的颜色指派都没有冲突,则在当前节点处选择第一个子树继续搜索,也就是为下一个顶点着颜色1,否则,对当前子树的兄弟子树继续搜索,也就是为当前顶点着下一个颜色,如果所有m种颜色都已经尝试过并且都发生冲突,则回溯到当前节点的父节点处,上一个顶点的颜色被改变(color[k]+=1),以此类推。
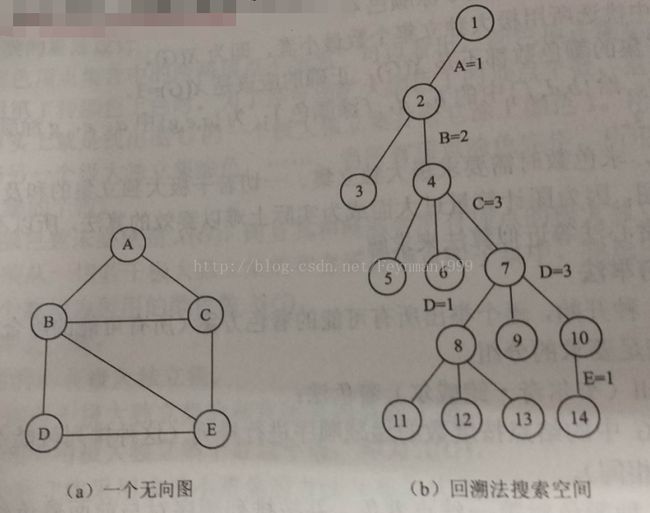
回溯法搜索空间图如下图所示:(题图无关)
代码示例
#include
using namespace std;
const int maxn=20;
int Map[maxn][maxn];
int color[maxn];//记录每个点的着色情况
bool ok(int k)//判断顶点k的着色是否发生冲突
{
for(int i=1;i=1)
{
color[k]+=1;
while(color[k]<=m)
{
if(ok(k)) break;
else color[k]++;//搜索下一个颜色
}//挑选合适颜色(不冲突)
if(color[k]<=m&&k==n){
//for(int i=1;i<=n;++i) printf("%d ",color[i]);
//printf("\n");
cnt++;
}
else if(color[k]<=m&&k
复杂度分析
图M着色问题用回溯法解决时,算法的时间上界可以通过计算解空间树种内结点的个数来估计,该问题中,解空间树中内结点数为n ,对于每一个结点,在最坏情况下,ok检查当前结点的每一个儿子所相应的颜色的可用性需耗时O(m *n);因此该方法的时间复杂度为: = nm(m^n-1)/(m-1)=O(nm^n);
本题中m=4 即为O(n* 4^n )
可以看出回溯法时间上就是在枚举,一共n个点,每个点4中可能颜色(4^n),然后每次判断这个点与n个点的合法性。回溯法代码较简洁,有深度优先搜索的思想。