数学奖章上的数学故事
其中许多是“单项奖”,奖励在某些方面(往往是用来命名的数学家有所建树的领域)成就卓著的数学家。如欧拉奖(Euler Prize)自1993 起在每年的国际组合数学年会上颁发给在组合数学领域有突出贡献的数学家。也有不少“终身成就奖”,著名的有2001 年设立的阿贝尔奖。该奖由挪威王室一年一度颁给杰出数学家,奖金达80 万美元,媲美诺贝尔奖奖金,是世界上奖金最高的数学奖。
>>>>
本文我们将从国际数学家大会四大奖项和国际数学教育大会两大奖项,欣赏奖章,了解相关的数学家和数学知识。

菲尔兹(John Charles Fields,1863-1932 年)
菲尔兹奖由加拿大数学家约翰• 查尔斯• 菲尔兹(John Charles Fields,1863-1932 年)建议设立。菲尔兹早年游学美国、欧洲,与诸多大数学家共事。其后返回加拿大致力于提升数学的地位。如在他努力下,1924 年世界数学家大会在加举行。他自上个世纪20 年代末开始筹备该奖,并遗嘱捐赠$47,000给奖项基金。菲奖在1936 年首颁;后从1950 年起每隔4 年颁发一次,奖励40 岁以下数学成就杰出者,且旨在鼓励获奖者进一步的研究。获奖者一般为2 至4 人。该奖有“数学界中诺贝尔奖”之称,其实它早期并无今日如此声誉,这很大程度上源于历届获奖者给它带来的荣耀。
菲尔兹奖包括一面金质奖章和一笔不算多的奖金(目前为15,000 加元)。奖章正面有古希腊数学家阿基米德的头像(Archimedes, 前287- 前212 年)和希腊文“ΑΡΧΙΜΗΔΟΥΣ”,意为“阿基米德的(头像)”;头像周边刻拉丁文“TRANSIRE SUUM PECTUS MUNDOQUE POTIRI”,此来源于一世纪罗马诗人马尼利乌斯(Manilius)的著作《天文学》,意为“超越他的心灵,掌握世界”。此外奖章设计者(Robert Tait McKenzie)名字之缩写RTM 及设计年份MCNXXXIII(即1933 年,第二个M 字母以N 代)也刻在奖章上。获奖者的名字则会被刻于奖章边轮。

菲奖章背面刻有意为“聚全球数学家,为杰出著作而颁”的拉丁文“CONGREGATI EX TOTO ORBE MATHEMATICI OB SCRIPTA INSIGNIA TRIBUERE”。文字和树枝的背景为球体嵌进圆柱体(“圆柱容球”)的示意图,这象征着阿基米德的得意之作《论球与圆柱》中最著名的一个结果:球与其外切柱体的面积(体积)之比为2 : 3。阿基米德对此如此骄傲,以致他希望人们在他的墓碑上刻下球与圆柱体的关系图。确实,阿基米德计算各种面积所用的“穷竭法”可以被视作后世微积分学所用“无穷小分析”的起源。
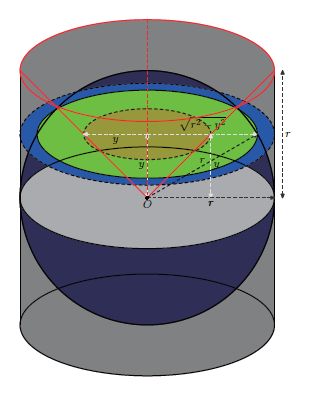
球与其外切柱体的面积(体积)之比为2 : 3 :若设球半径为r,则球面积为4πr2,体积4/3πr³ ;而其外切柱体面积为6πr2,体积为2πr³
传说正沉思于几何问题的阿基米德被鲁莽无知的罗马士兵杀死之后,罗马将军马塞勒斯悲伤不已,不但给阿基米德立墓,备极哀荣,并按他生前的愿望在碑上刻球内切于圆柱的图形。在公元前73 年,时任西西里岛财务官的罗马著名政治家、哲学家西塞罗(Marcus Tullius Cicero, 前106- 前43 年)去叙拉古(Syracuse)探访阿基米德之墓。其时阿基米德去世才137 年,当地人却已对阿基米德之墓一无所知,否认有这样一个墓。通过一番搜索,西塞罗终在杂草丛中凭此球内切圆柱图案辨认出阿基米德的墓,并派人去清理繁芜,铺砌道路。西塞罗在他的文章中写道,找到阿基米德之墓后,他告诉叙拉古人,此刻他和叙拉古最杰出的人在一起,而这正是他一直在寻求的。后来一些画家还将此刻情景凝固在油画中。其中著名的有美国画家本杰明•威斯特(Benjamin West, 1738-1820)1797 所作的油画“西塞罗发现阿基米德之墓”(1804 年他另作一幅稍有差别的画)。两个名人穿时空的重逢确是值得纪念的。这种对文明的尊重弥足珍贵的另一个原因是对数学家的尊重在西塞罗那个时代是少见的。西塞罗曾写道“几何学在希腊人中享有极高声誉,没有什么比数学更加荣光的了;但我们(罗马人)却只满足于那些用来计算和测量的数学知识”。

今日意大利西西里岛阿基米德家乡叙拉古的“阿基米德的坟墓”遗址
类似于阿基米德的“穷竭法”和圆柱容球的比例2 : 3,我国三国时代魏国数学家刘徽也应用类似的极限思想求出了圆面积、一些锥体(如阳马与鳖臑)的体积。而且他还在评注我国算术名著《九章算术》时正确地猜测了球体积与其外切牟合方盖体积之比等于圆与其外接正方形的面积之比(即π :4)。这里所谓的“牟合方盖”是一个立方体从纵横两个方向做内切圆柱的共同部分,因其外型酷似上下相对(牟合)的方伞(盖)。中国家庭日常生活中常用的食物罩就类似牟合方盖的一半。
原来在《九章算术》的“少广”章中记有“开立圆术”,认为直径为D的球体积公式为
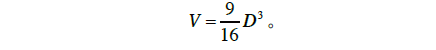
如果将π 取值为3,则该公式相当于认为球体积与其外切圆柱体积之比为3:4。刘徽指出这是错误的,但他自己没能求出牟合方盖的体积从而得出正确的球体积计算公式,而是将这个问题留给了后人,“以俟能言者”。
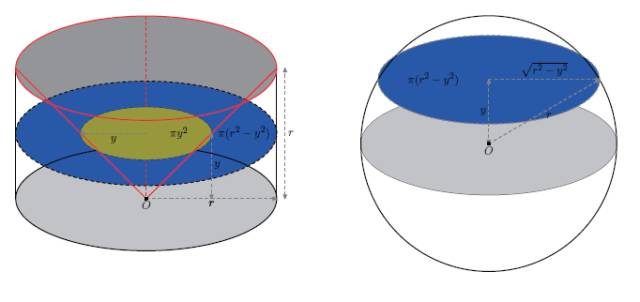
半球体积与圆柱体去掉锥体剩余部分体积相同(横截面(图中蓝色部分)面积相同)
刘徽去世之后200 余年,南北朝时期的祖冲之、祖暅父子共同提出了祖暅原理:所有等高处横截面积相等的两个同高立体,其体积也必然相等(“缘幂势既同,则积不容异”)。该原理在西方常被称为卡瓦列里原理,因由意大利几何学家卡瓦列里(Bonaventura Francesco Cavalieri, 1598 年-1647 年)重新发现。这可以看作是微积分学发展历程中自阿基米德的穷竭法之后的一大进步。祖氏父子正是利用此原理算出牟合方盖的体积从而得出球体体积。

刘徽提出的球体体积与牟合方盖的体积之比则是祖暅原理的直接推论:因为我们可将球体当作由横截的圆累积而成;若将这些横截圆改为外接该圆的正方形,则所得立体即是牟合方盖。我们这里仅简单介绍如何用祖暅原理来理解阿基米德提出的比例。
在底面半径和高均为r 的圆柱体中倒立一个以圆柱体上表面为底,下底面圆心为顶点的圆锥。易由勾股定理得知半径为r 的半球“赤道”上方y处横截面(半径为 √(r2—y2) 的圆)的面积为π(r2 - y2) ;而等高处圆柱体的横截面的面积(恒为πr2)去掉锥体的横截面积(πy2)为π(r2- y2)。由祖暅原理,半球体积等于圆柱体中除去圆锥体所剩部分之体积。我们知道内嵌圆锥体体积是柱体体积的三分之一,因此半球体积是三分之二倍此圆柱体体积。
奈望林纳奖
奈望林纳奖由国际数学联盟于1981 年设立,奖励在信息科学的数学方面有突出贡献的年轻数学家。它类似于菲尔兹奖,得奖者必须在获奖那一年不大于40 岁。该奖包括一枚奖章和部分奖金,每四年在国际数学家大会颁发,且获奖者的名字也会被刻在奖章边轮。奈望林纳奖于1982 年首颁,有“计算机科学中诺贝尔奖”之称。奈望林纳奖是以纪念在1980 年去世的芬兰最著名的数学家之一罗尔夫• 奈望林纳(Rolf Herman Nevanlinna, 1895-1980 年)。奈望林纳在函数论方面贡献卓著,且在20 世纪50 年代开启了芬兰的计算机项目。

1982 年,国际数学联盟接受赫尔辛基大学对该奖的资助。奖章正面为奈望林纳的头像以及文字“ROLF NEVANLINNA PRIZE”(“奈望林纳奖”)以及很小的字符“RH 83”(示意此奖章由设计者 Raimo Heino 于1983 年首次铸造),反面的两个图案都和赫尔辛基大学有关。奈望林纳是赫尔辛基大学的教授,并曾任校长。右下角是赫尔辛基大学的校徽,环绕校徽有赫尔辛基大学的名字“UNIVERSITAS HELSINGIENSIS”。左上角是文字“Helsinki”的编码,这和该奖的表彰内容相得益彰。例如,2010 年获得奈望林纳奖的Daniel Spielman 的一个主要贡献即是关于编码理论的。
高斯奖
高斯奖由德国数学家联合会和国际数学联盟共同设立,以纪念“数学王子”高斯(Carl Friedrich Gauss, 1777-1855),主要用于奖励在数学之外的应用领域,如经济、技术乃至日常生活中有深刻影响的数学家。
高斯奖设立于2002 年,并于2006 年在马德里召开的第25 届国际数学家大会上首次颁发。高斯奖包含一笔奖金和一枚奖章;奖金目前为一万欧元,资金来源于1998 年在柏林召开的ICM 的结余。高斯奖章正反图案均以数学中的基本元素点、线、曲线来构图。正面勾勒出高斯的头像,并刻文“For Applications of Mathematics”(“为应用数学”);反面为一曲线、一点和一方框组成的图以表示高斯的伟大成就之一:以最小二乘法来确定行星的轨迹。这是应用数学的典范。

1801 年元旦,意大利天文学家皮亚齐(Giuseppe Piazzi)发现了后来被命名为谷神星的小行星。皮亚齐跟踪观测了40 天后由于谷神星运行至太阳背后而丢失。科学家们开始了利用皮亚齐的观测数据来预测谷神星出现位置的竞赛。时年只有24 岁的高斯运用早在1794 年就创立的最小二乘法理论,准确地预测了谷神星的轨迹。同年底,天文学家Zack 在很接近高斯预测的位置上重新发现了谷神星。
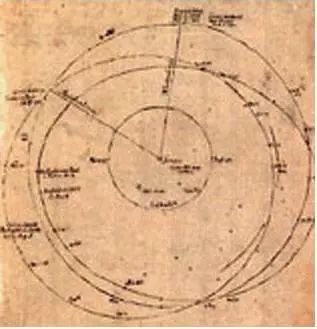
高斯绘谷神星的轨迹图
1809 年高斯在题为《围绕太阳沿圆锥曲线轨道公转的天体的运动理论》一文中,正式发表了最小二乘法理论。此前法国的勒让德(Adrien-Marie Legendre)也独立发现了最小二乘法原理。不过高斯对最小二乘法的贡献确实很大。他在1822 年证明了回归分析中最小二乘法在一定意义上是最优的。他还利用最小二乘理论,得出了拉普拉斯等人苦思不得的误差分布——现在常称的高斯分布。德国曾经流通的10 马克纸币,以及一枚纪念高斯的纪念币上,都有象征正态分布密度函数的“钟形”曲线图。
获得首届高斯奖的日本著名数学家伊藤清(Kiyoshi Itō, 1915-2008)的工作即是高斯奖表彰对象的范例。伊藤清揭示了随机王国的牛顿定律,开创了“随机分析”学。获得1997 年的诺贝尔经济学奖的美国经济学家Robert Merton 和Myron Scholes 提出进行期权定价的Black- Scholes 模型即基于伊藤清的工作。虽然早在1900 年,法国数学家Bachelier 就已经在他的博士论文中应用布朗运动来研究金融问题了,但伊藤清还是对他自己所研究的纯粹概率理论能在金融数学里有着深刻的应用感到吃惊。

2006 年9 月,国际数学联盟主席鲍尔爵士前往日本将首届高斯奖颁给伊藤清
陈省身奖
陈省身奖是首个以华人名字命名的国际数学大奖,它由陈省身基金和国际数学联盟共同设立,以纪念我们都很熟悉的数学家陈省身(Shiing-Shen Chern, 1911-2004),奖励给那些在数学领域有杰出终身成就的个人。陈省身奖于2010 年在印度海德拉巴市(Hyderabad)举行的第26 届国际数学家大会上首颁。

天津南开大学陈省身楼旁的陈省身先生及其夫人郑士宁女士的纪念碑(附:左下角为碑顶)(王龙 摄)
陈奖含一笔奖金和一枚奖章。奖金为50 万美元,一半奖励给数学家本人,另一半奖金由获奖人捐助给一些支持数学的研究、教育和其它活动的社会机构,以推动数学的发展。
陈奖也获得哈里斯• 西蒙斯基金的支持。西蒙斯(James Harris Simons,1938 年出生)算是陈省身先生的学生,也是他数学上的“六个朋友”(参《陈省身传》)之一,他们曾合作得到几何理论对理论物理学具有重要意义的Chern-Simons 理论。西蒙斯在1970 年代放弃数学去经商,现为著名的投资家。他还大力支持科学事业,特别是数学事业。
陈省身奖章正面为时年73 岁的陈省身头像,左为陈先生的中文签名,右为英文签名,右边签名下方刻“1911-2004”,表明他的出生和去世年份。奖章反面为陈省身1944 年证明的广义高斯- 博内定理(又名陈- 高斯- 博内定理)
这个公式的最简单情形就已经足够有趣:曲面上测地三角形的总曲率(高斯曲率的曲面积分)等于它的三角之和与π 的差。因此正曲率曲面(如球面)上的三角形三角之和大于π,而负曲率曲面(如双曲几何曲面)上的三角形三角之和小于π。零曲率曲面(欧几里得平面)上,三角之和正好为π。
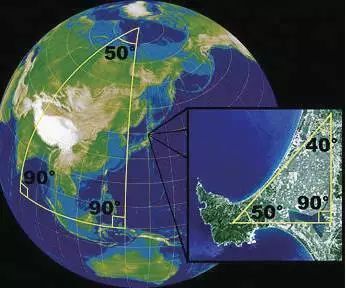
地球上大范围三角之和大于π,而局部三角可以近似看作平面三角形,其和等于π
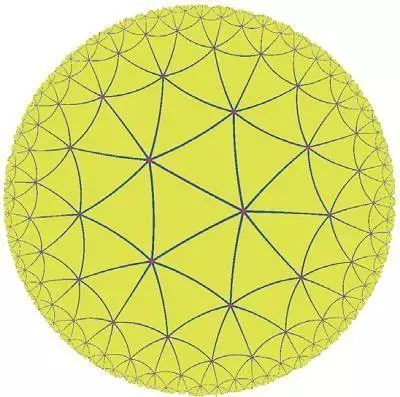
双曲三角之和小于π
与陈奖章类似的是最近在南开大学省身楼旁揭幕的陈氏夫妇纪念碑(今年为陈省身诞辰100 周年)。纪念碑正面为黑色花岗岩造“黑板”,上刻陈手书高斯- 博内公式的证明,下刻陈省身夫妇的姓名。纪念碑整体横截面为(双曲几何曲面上的)曲边三角形,示意前述高斯- 博内公式的简单情形。

∑编辑 | Gemini
选自 | 哆嗒数学网
算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域
经采用我们将奉上稿酬。
投稿邮箱:[email protected]
