非递归式（zkw）线段树详解（一）

线段树，是在信息学各类比赛中经常出现的数据结构之一
普通的线段树大家应该都会，下面来介绍一种不需要递归的线段树

zkw线段树
出自：《统计的力量》-张昆玮

zkw线段树不同于普通线段树的地方在于：它采用堆结构，构造一颗满二叉树（也可以说是完全二叉树），而二叉树的最后一层则是各个节点。

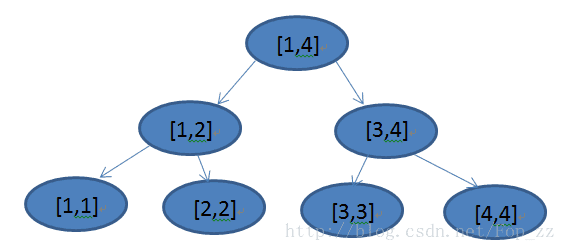
注意：zkw线段树必须是点树，即完全闭区间
普通线段树中的修改需要去查询节点，并分为三类：
完全覆盖，在左区间，在右区间
那么换个方法，自底向上更新呢？
这就是zkw的想法

下面以 单点修改 区间求值为例子
建树：
采用堆结构，取到log(n)-1层最后一个节点，例如上图中，[3,4]节点的标号为3。
那么从3+1开始到3+4，就是1-4四个点的位置了。
好。我们直接把值丢到tree[4~7]中就可以了。。。。
同时向上更新：tree[i]=tree[i*2]+tree[i*2+1]
代码：

inline void up(int x)
{
    tr[x]=tr[x<<1]+tr[x<<1|1];
}
inline void build()
{
    for(M=1;M<=n+1;M<<=1);
    for(int j=M+1;j<=M+n;j++)
        scanf("%d",&tr[j]);
    for(int j=M-1;j;j--)
        up(j);
}

上面代码中，M为log(n)-1层的最后一个节点的下标

更新：
单点更新，更新第k个点同时更新所有k的祖先

inline void update(int x,int y)
{
    for(tr[x+=M]+=y,x>>=1;x;x>>=1)
        up(x);
}

查询：
查询s-t区间的和
这个略微复杂，考虑s和t的区间位置：
当s为左儿子，则s的父亲节点被s-t包含，反之该区间内只有s被包含同理 当t为右儿子，则t的父亲节点被s-t包含
很容易理解 可以直接加上t和s的兄弟节点来得到父亲节点的值，同时把s和t上移
当s和t是兄弟时，说明s-t的区间中所有数已经被全部包含
这里可以用到一些位运算优化：
用&确定左右子树，用^确定是否为兄弟关系

inline int  query(int s,int t)
{
    int ans=0;
    s=s+M-1;t=t+M+1;
    for(;s^t^1;s>>=1,t>>=1)
    {
        if(~s&1)ans+=tr[s^1];
        if(t&1) ans+=tr[t^1];
    }
    return ans;
}

然后。。整个代码就写完了

#include
#include
#include
using namespace std;
int M;
int tr[1500001],n,m;
inline void up(int x)
{
    tr[x]=tr[x<<1]+tr[x<<1|1];
}
inline void build()
{
    for(M=1;M<=n+1;M<<=1);
    for(int j=M+1;j<=M+n;j++)
    {
        int t;
        scanf("%d",&t);
        tr[j]=t;
    }
    for(int j=M-1;j;j--)
        up(j);
}
inline void update(int x,int y)
{
    for(tr[x+=M]+=y,x>>=1;x;x>>=1)
        up(x);
}
inline int  query(int s,int t)
{
    int ans=0;
    s=s+M-1;t=t+M+1;
    for(;s^t^1;s>>=1,t>>=1)
    {
        if(~s&1)ans+=tr[s^1];
        if(t&1) ans+=tr[t^1];
    }
    return ans;
}
int main()
{
    cin>>n>>m;
    build();
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        if(x==1)update(y,z);
        else    printf("%d\n",query(y,z));
    }
}

是不是比普通线段树的代码简短好多。。同时运行速度比普通线段树快2-3倍

---

---

接下来…..恶心的来了

区间修改
原文中说是要利用的。。前缀的前缀和。。。
本蒟蒻语文不好。。是在不懂什么意思- -
但是大概是利用差分思想（不是积分差分的那个

一个简单的例子：区间修改 单点求值
（区间修改 区间求和下次再说咯。。
我们可以发现，在这个问题中，如果一个个单点修改的复杂度是nlogn，好像还不如暴力。。
大家如果学过树状数组，应该好理解一些。
我们可以把每个点的值，化为从根节点到那个点的链上所有标记之和
上面说了标记。。没错。。类似于lazy标记
但是这个lazy标记不会被pushdown反而只会upupup
考虑这样的情况

求链上的和，我们就可以把这棵树改造为

上述操作代码：

int mi=min(tr[s],tr[s^1]);
tr[s]-=mi;
tr[s^1]-=mi;
tr[s>>1]+=mi;
s>>=1;

那么这样，我们就可以只记录它的偏移量，而不直接记录值
于是就构造了一颗。。标记树
对于单点求和，确实没有必要记录下每个点的值，但是如果要区间求值就需要建两棵zkw树了。。比较烦，下次讲
那么求单点的值也是很简单的啦。下面来分步讲解
建树：
同上，只是更新1-M之间的过程改一下

inline void build()
{
    for(M=1;M<=n+1;M<<=1);
    for(int i=M+1;i<=M+n;i++)
        scanf("%d",&tr[i]);
    int t=M+n;
    for(t=M;t;t--)
    {
        int mi=min(tr[t<<1],tr[t<<1|1]);tr[t<<1]-=mi;tr[t<<1|1]-=mi;tr[t]+=mi;
    }
}

更新：
由于要处理区间，可以参考之前的求区间和部分程序
只不过要加上那个up，并且求值改为修改

inline void add(int s,int t,int v)
{
    for(s=s+M-1,t=t+M+1;s^t^1;s>>=1,t>>=1)
    {
        if(~s&1)   tr[s^1]+=v;
        if(t&1)     tr[t^1]+=v;
        int mi=min(tr[s^1],tr[s]);tr[s]-=mi;tr[s^1]-=mi;tr[s>>1]+=mi;
        mi=min(tr[t^1],tr[t]);tr[t]-=mi;tr[t^1]-=mi;tr[t>>1]+=mi;
    }
    while(s)
    {
        int mi=min(tr[s],tr[s^1]);tr[s]-=mi;tr[s^1]-=mi;tr[s>>1]+=mi;s>>=1;
    }
}

好吧我知道这个有点恶心。。但是仔细看还是容易理解的
查询：
这个简单了啊
一条链上全部加起来

inline int query(int x)
{
    int sum=0,p=M+x;

    while(p)
        sum+=tr[p],p>>=1;
    return sum;
}

又写完了咯

#include
#include
#include
using namespace std;
int M;
int tr[2000001],n,m;
inline void build()
{
    for(M=1;M<=n+1;M<<=1);
    for(int i=M+1;i<=M+n;i++)
        scanf("%d",&tr[i]);
    int t=M+n;
    for(t=M;t;t--)
    {
        int mi=min(tr[t>>1],tr[t>>1|1]);tr[t>>1]-=mi;tr[t>>1|1]-=mi;tr[t]+=mi;
    }
}
inline void add(int s,int t,int v)
{
    for(s=s+M-1,t=t+M+1;s^t^1;s>>=1,t>>=1)
    {
        if(~s&1)    tr[s^1]+=v;
        if(t&1)        tr[t^1]+=v;
        int mi=min(tr[s^1],tr[s]);tr[s]-=mi;tr[s^1]-=mi;tr[s>>1]+=mi;
        mi=min(tr[t^1],tr[t]);tr[t]-=mi;tr[t^1]-=mi;tr[t>>1]+=mi;
    }
    while(s)
    {
        int mi=min(tr[s],tr[s^1]);tr[s]-=mi;tr[s^1]-=mi;tr[s>>1]+=mi;s>>=1;
    }
}
inline int query(int x)
{
    int sum=0,p=M+x;

    while(p)
        sum+=tr[p],p>>=1;
    return sum;
}
int main()
{
    cin>>n>>m;
    build();
    for(int i=1;i<=m;i++)
    {
        int x;
        scanf("%d",&x);
        if(x==1)
        {
            int s,t,v;
            scanf("%d%d%d",&s,&t,&v); 
            add(s,t,v);
        }
        else
        {
            int s;
            scanf("%d",&s);
            printf("%d\n",query(s));
        }
    }
}

感谢读到这里