重新理解梯度下降法(Gradient Descent)及其相关优化方法
梯度下降法广泛的应用在无约束优化问题的求解中,比如线性回归、神经网络等等。之前在学习Stanford机器学习-Linear Regressioon with One Variable(3)时对于梯度下降有了初步的理解,但是对于梯度下降法的多种类型,以及背后的数学原理理解的并不是很清楚,希望通过这个专项的学习,对于梯度下降法可以有一个深入的学习。
所需的数学知识
对于其中涉及的导数、偏导数、梯度等基础知识,本科学过微积分的应该都清楚,其中很重要的一点就是明白梯度的含义:从几何意义上看,它是指函数变化最快的方向!
为什么需要梯度下降?
在实际的问题中,虽然它们存在着最优解,但是往往不太好直接求出,或者很难求出全局的最优解,这时候就只能退而求其次,找出局部的最优解。比如在线性回归中,当情况简单时我们可以使用最小二乘法直接求出解。但是在处理实际问题时,因为某些原因,往往很难使用最小二乘法,这时梯度下降就可以很好的解决问题。
引入
在理解梯度下降时,使用最多的就是下山的例子了。假设你位于山上的某一个位置,想要找到某条好的路径下山,但是由于能见度很低,你无法直接通过眼睛的观察找出一条下山最快的路。这时你只能一步一步的来。从你当前的位置开始,寻找坡度最大的方向,然后朝这个方向走一段距离,然后停住脚步,重复的使用这种思想找路,最终就可以到达山底。
而梯度下降就是这么一种思路,在解决某一任务时,往往需要对其进行建模,使用合适的算法进行解决。其中表示模型的往往是一个函数,我们需要做的就是找到这个函数的最小值。对比来看,函数就相当于山,梯度就是下山最快的方向,山底就是局部的最小值。整个一步一步下山的过程就是不断迭代使用梯度下降求解函数的局部最小值的过程。

梯度下降法(Batch Gradient Descent)
我们以最基本的线性回归为例来学习梯度下降,从而将其中的思想推广的其他算法的应用中。
假设我们有 x i , i = 1 , 2 , 3 , . . . , n x_{i},i=1,2,3,...,n xi,i=1,2,3,...,n诸多数据点,目标是希望找到最优的拟合超平面(在2-D情况下表示为一条拟合直线),其中超平面用 h θ ( x 1 , x 2 , . . . x n ) = θ 0 + θ 1 x 1 + . . . + θ n x n h_\theta(x_1, x_2, ...x_n) = \theta_0 + \theta_{1}x_1 + ... + \theta_{n}x_{n} hθ(x1,x2,...xn)=θ0+θ1x1+...+θnxn表示, i = 1 , 2 , 3 , . . . , n i=1,2,3,...,n i=1,2,3,...,n,其中 θ i \theta_{i} θi是模型的未知的参数, x i x_{i} xi表示数据中的各个特征,为了方便公式的推导,令 x 0 = 1 x_{0}=1 x0=1,这样关于 θ i \theta_{i} θi的表达式如下所示: h θ ( x 0 , x 1 , . . . x n ) = ∑ i = 0 n θ i x i h_\theta(x_0, x_1, ...x_n) = \sum\limits_{i=0}^{n}\theta_{i}x_{i} hθ(x0,x1,...xn)=i=0∑nθixi
对于新的数据,这里使用均方误差来衡量预测值和真实值之间的差距,所以损失函数可以定义为如下的形式:
J ( θ 0 , θ 1 . . . , θ n ) = 1 2 m ∑ j = 0 m ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n ( j ) ) − y j ) 2 J(\theta_0, \theta_1..., \theta_n) = \frac{1}{2m}\sum\limits_{j=0}^{m}(h_\theta(x_0^{(j)}, x_1^{(j)}, ...x_n^{(j)}) - y_j)^2 J(θ0,θ1...,θn)=2m1j=0∑m(hθ(x0(j),x1(j),...xn(j))−yj)2
下面需要做的就是使用梯度下降法来求出损失函数的最小值,它所对应的参数 θ i \theta_{i} θi( i = 1 , 2 , 3 , . . . , n i=1,2,3,...,n i=1,2,3,...,n)就是最优的模型参数。
梯度下降法的算法步骤如下所示:
-
确定算法的终止阈值 ϵ \epsilon ϵ和学习率(learning rate) α \alpha α
ϵ \epsilon ϵ:表示算法停止的条件,当梯度下降的变化值小于 ϵ \epsilon ϵ时,我们就认为它已经到达了局部的最小值,没有必要继续进行下去
α \alpha α:它表示梯度下降过程中前进的长度,即下山时每一步的步长 -
确定当前位置的梯度,对于任意一个参数 θ i \theta_{i} θi它的梯度表示如下所示: ∂ ∂ θ i J ( θ 0 , θ 1 . . . , θ n ) \frac{\partial}{\partial\theta_i}J(\theta_0, \theta_1..., \theta_n) ∂θi∂J(θ0,θ1...,θn)
-
确定下降的距离大小,用 α ∂ ∂ θ i J ( θ 0 , θ 1 . . . , θ n ) \alpha\frac{\partial}{\partial\theta_i}J(\theta_0, \theta_1..., \theta_n) α∂θi∂J(θ0,θ1...,θn)表示
-
观察所有 θ i \theta_{i} θi的梯度值是否小于设定的阈值 ϵ \epsilon ϵ,如果都小于 ϵ \epsilon ϵ,则算法终止,否则需要使用下面的步骤更新参数 θ i \theta_{i} θi
-
θ i \theta_{i} θi更新公式如下所示 θ i = θ i − α ∂ ∂ θ i J ( θ 0 , θ 1 . . . , θ n ) \theta_i = \theta_i - \alpha\frac{\partial}{\partial\theta_i}J(\theta_0, \theta_1..., \theta_n) θi=θi−α∂θi∂J(θ0,θ1...,θn)代入 J ( θ 0 , θ 1 . . . , θ n ) J(\theta_0, \theta_1..., \theta_n) J(θ0,θ1...,θn)的表达式后如下所示 θ i = θ i − α 1 m ∑ j = 0 m ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n j ) − y j ) x i ( j ) \theta_i = \theta_i - \alpha\frac{1}{m}\sum\limits_{j=0}^{m}(h_\theta(x_0^{(j)}, x_1^{(j)}, ...x_n^{j}) - y_j)x_i^{(j)} θi=θi−αm1j=0∑m(hθ(x0(j),x1(j),...xnj)−yj)xi(j)
更新完之后转向步骤2,不断迭代进行,直至算法收敛。
另外也可以使用矩阵的形式表述算法的过程,可见矩阵来描述梯度下降
基本的梯度下降过程就是这样的一个形式
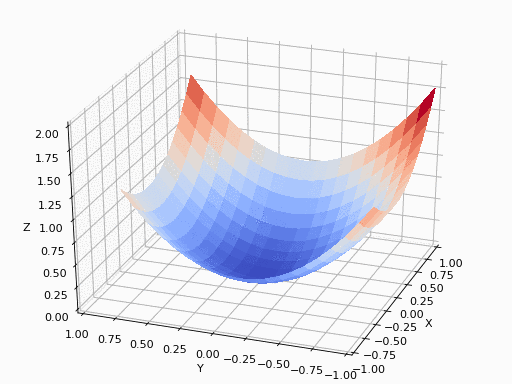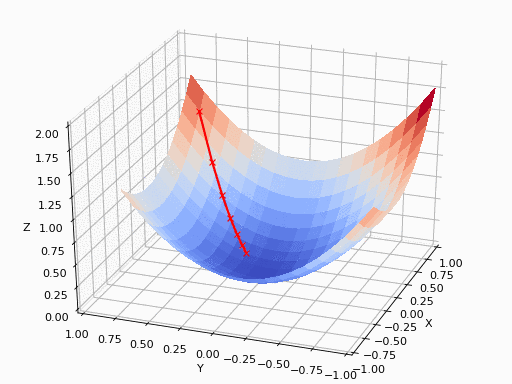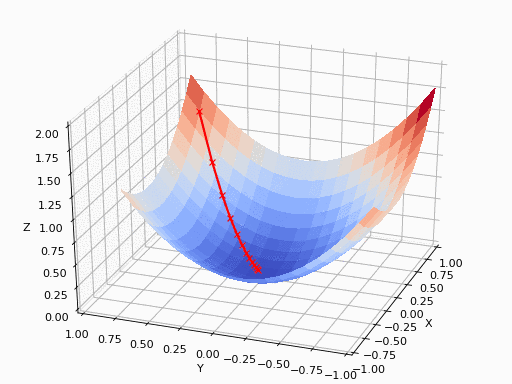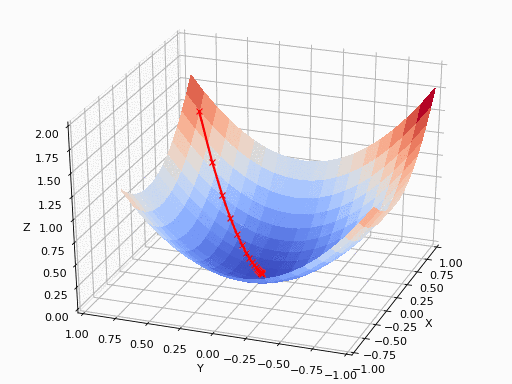
其中需要注意:
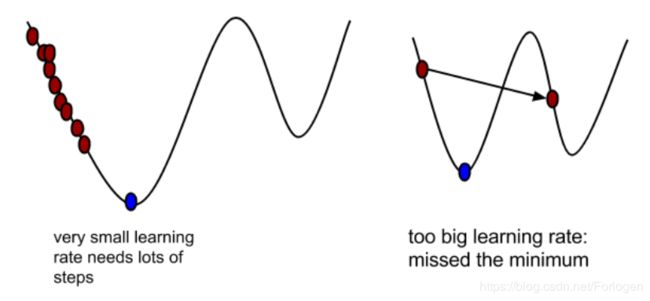
- α \alpha α的选择,如果步长太大,在局部最小值附近可能会不断地振荡,无法收敛到局部的最小值;如果取值太小,则下降的速度太慢,导致算法需要很长的时间执行结束。
- θ i \theta_{i} θi的选择: θ i \theta_{i} θi不同,最终求得的函数的最小值也就可能不同。因此我们可以通过运行多次具有不同 θ i \theta_{i} θi的算法来求出不同的最小值,最后选择能得到最优的函数最小值的初始化参数 θ i \theta_{i} θi
在二维的线性回归问题中使用批量梯度下降的代码:
#梯度下降法计算回归系数。xArr为属性数据集,每行为一个对象。yArr为结果数据集,每行为一个对象的结果。
def gradAscent(xArr,yArr):
xMatrix = np.mat(xArr)
yMatrix = np.mat(yArr).reshape(len(yArr),1)
m, n = np.shape(xMatrix)
alpha = 0.001
maxCycles = 500
#初始化权重列向量
weights = np.ones((n,1))
for k in range(maxCycles):
#梯度上升矢量化公式,计算预测值(列向量)
h = xMatrix * weights
#计算误差
error = h - yMatrix
# 调整回归系数
weights = weights - alpha * 2 * xMatrix.T * error
return weights.getA()
随机梯度下降(Stochastic Gradient Descent)
但是在批量梯度下降中,也存在着一些问题:
- 每一次更新参数时会使用全部的数据,使得在大规模数据集上进行时存在大量的冗余计算,导致计算量巨大,算法速度慢
- 无法实现在线的更新,只能使用固定的数据进行学习
- 算法一旦到达了梯度值等于零的地方,不管是否是局部的最小值点,它都无法继续再往前走,这个值可能是局部的最小值点,也可能是如下所示的“鞍点”(如下图中两条虚线的交汇点)

所以一个极端的解决办法就是,在每一次参数更新时不是使用全部的数据,而是随机的从中选择一个,具体的更新公式如下所示:
θ i = θ i − α ∇ θ J ( θ ; x i ; y i ) \theta_i = \theta_i - \alpha∇_{\theta}J(\theta;x^{i};y^{i}) θi=θi−α∇θJ(θ;xi;yi)
-
优点:
- 虽然迭代的次数会增加,但是每一次的速度将会很快
- 因为每次只选择一个数据,故无冗余计算
- 实现了在线学习,新的数据随时可加入数据集,对运算过程不造成影响
-
缺点:
在二维线性回归问题中使用随机梯度下降代码:
#随机梯度下降法计算回归系数
def randgradAscent(xArr,yArr):
xMatrix = np.mat(xArr)
yMatrix = np.mat(yArr).reshape(len(yArr),1)
m, n = np.shape(xMatrix)
maxCycles = 100
weights = np.ones((n,1))
for i in range(maxCycles):
for k in range(m):
# 降低alpha的大小,每次减小1/(j+i)。刚开始的时候可以步长大一点,后面调整越精细
alpha = 4 / (1.0 + i + k) + 0.01
#随机梯度上升矢量化公式,计算预测值y
h = xMatrix[k] * weights
#计算误差
error = h - yMatrix[k]
# 调整回归系数
weights = weights - 2*alpha * xMatrix[k].T * error
return weights.getA()
小批量梯度下降(mini-batch Gradient Descent)
它是上面两种方法的一个折中,每一次更新的时使用的是很小的一部分数据,假设从 m m m个样本中选择 x x x个更新,假设随机选择的数据的起始位置是 t t t,对应的更新公式为: θ = θ − η ∇ θ J ( θ ; x ( i ; i + n ) ; y ( i ; i + n ) ) \theta=\theta-\eta ∇_{\theta} J(\theta;x^{(i;i+n)};y^{(i;i+n)}) θ=θ−η∇θJ(θ;x(i;i+n);y(i;i+n))
- 优点
- 降低参数更新时的方差,使的收敛过程更稳定
- 可以充分利用现有的深度学习库中高度优化的矩阵操作进行更有效的计算
关于基本梯度下降法所存在问题的反思
虽然上面的三种梯度下降法最后可以得到一个局部的最小值,但仍存在一些问题:
- 学习率 α \alpha α的选择问题:上面已经提到过
- 虽然可以在开始处设置好 α \alpha α的随时刻变化的计划表,但是无法实现根据具体的情况进行实时的更新
- 无法利用数据中特征间的关系:在稀疏数据或是特征之间差距较大时,得到的结果往往不太好
- 不能很好的处理非凸优化问题的最优解,很容易受困于鞍点处
因此针对这些问题,学术界提出了如下的多种改进的算法。
关于梯度下降的相关改进算法
momentum
在前面的梯度下降中,下降的过程是计算一次梯度走一步,迭代的进行,直到局部的最小值处。这样做的缺点就是学习的过程会很慢。想象一下真实情况下一个大石球从山上滚下来的过程,它会越滚越快,迅速的达到山底。而动量法就是基于这样的一个思路,它使得在梯度方向不变的维度上速度加快,在梯度方向改变的维度上放慢速度,结果会帮助SGD加快收敛,并减少在局部最小值处的振荡。
具体的思想如下图所示

那么将A作为起始点,首先计算A处的梯度 ∇ a ∇_{a} ∇a,然后按照梯度下降到B点: θ n e w = θ − α ∇ a \theta_{new}=\theta-\alpha∇_{a} θnew=θ−α∇a接着就是带动量的梯度下降。在B点梯度有一个衰减值 γ \gamma γ一般取值0.9。B点的参数更新公式为: v t = γ v t − 1 + α ∇ b v_{t} = \gamma v_{t-1}+\alpha∇_{b} vt=γvt−1+α∇b θ n e w = θ − v t \theta_{new}=\theta-v_{t} θnew=θ−vt
其中 v t − 1 v_{t-1} vt−1表示之前所积累的动量和。
Nesterov accelerate gradient(NAG)
在动量法中,小球是盲目的沿着坡往下滚,我们希望它更聪明一点,比如再遇到坡时可以放慢速度。而NAG就是实现了这样的一种思路,在参数进行更新计算梯度时,它使用了 θ − γ v t − 1 \theta-\gamma v_{t-1} θ−γvt−1来替代 θ \theta θ,使得计算时是在未来的某个位置,而不是当前的位置,通过这种方法得到关于未来某个位置的近似。
参数的更新公式如下: v t = γ v t − 1 + α ∇ J ( θ − γ v t − 1 ) v_{t}=\gamma v_{t-1}+\alpha ∇J(\theta-\gamma v_{t-1}) vt=γvt−1+α∇J(θ−γvt−1) θ = θ − v t \theta=\theta-v_{t} θ=θ−vt
下面我们通过一个图来形象的看一下更新公式:

蓝色部分是前面动量法的过程,而NAG同样也是在先前的累积的梯度方向做一个跳跃(如棕色向量所示),但是它又进行了一个修正(红色向量所示),得到最终的下降方向(绿色部分所示),这样做可以避免走得太快。
Adagard
前面的各种算法的 α \alpha α是在算法开始之前就设置好的,并且不会随着过程所改变,而且可以随着损失函数的梯度变化来调整下降的速度,但是仍然无法根据不同重要性的参数进行不同程度的更新。
而Adagard 解决了这个问题,它通过在不同的迭代次数 t t t,对于每一个参数都会有不同的 α \alpha α。具体而言,对低频出现的参数进行大的更新,对高频出现的参数进行小的更新,因此适合处理稀疏数据。
假设在第 t t t次迭代时,参数 θ i \theta_{i} θi的梯度为 g t , i = ∇ J ( θ t , i ) g_{t,i}=∇J(\theta_{t,i}) gt,i=∇J(θt,i)
在随机梯度下降中,参数的更新公式为: θ t + 1 , i = θ t , i − α g t , i \theta_{t+1,i}=\theta_{t,i}-\alpha g_{t,i} θt+1,i=θt,i−αgt,i而在Agarda中参数的更新公式为 θ t + 1 , i = θ t , i − α G t , i i + ϵ g t , i \theta_{t+1,i}=\theta_{t,i}-\frac{\alpha}{\sqrt{G_{t,ii}+\epsilon}}g_{t,i} θt+1,i=θt,i−Gt,ii+ϵαgt,i
其中 G t G_{t} Gt是一个对角阵,其中对角线上 i , i i,i i,i的元素是从一开始到 t t t时刻目标函数对于参数 θ i \theta_{i} θi梯度的平方和。 ϵ \epsilon ϵ是一个平滑项,以避免分母为 0 的情况,它的数量级通常在 1 e − 8 1e-8 1e−8。如果不开方的话,这个算法的表现会变得很糟。
-
优点:
- 不需要对每个 α \alpha α手工地调节。在其他的大多数算法中一般取默认值如 0.01
- 可以很好的处理稀疏数据,提高了SGD的鲁棒性
-
缺点:在分母上的项中积累了平方梯度和。因为每次加入的项总是一个正值,所以累积的和将会随着训练过程而增大。这会导致 α \alpha α不断缩小,并最终变为一个无限小值,使得算法已经不能从数据中学到额外的信息
Adadelta
它只要是解决了Adagard中 α \alpha α不断单调下降导致最后无法学习到新东西的问题。相比计算之前所有梯度值的平方和,Adadelta 法仅计算在一个大小为 w w w的时间区间内梯度值的累积和。
它并不会存储之前 w w w个梯度的平方值,而是计算关于过去梯度值的衰减均值(decade average)。当前时间 t t t的梯度均值 E [ g 2 ] t E[g^{2}]_{t} E[g2]t是基于过去梯度均值和当前梯度值平方的加权平均,其中 γ \gamma γ是类似上述动量项的权值,同样设置为0.9。
E [ g 2 ] t = γ E [ g 2 ] t − 1 + ( 1 − γ ) g t 2 E[g^2]_{t}=\gamma E[g^2]_{t-1}+(1-\gamma)g^2_{t} E[g2]t=γE[g2]t−1+(1−γ)gt2
将SGD 更新规则写为关于参数更新向量 的形式:
△ θ t = − α g t , i △\theta_{t}=-\alpha g_{t,i} △θt=−αgt,i θ t + 1 = θ + △ θ t \theta_{t+1}=\theta+△\theta_{t} θt+1=θ+△θt
由此,刚刚在 Adagrad 法中推导的的参数更新规则的向量表示,变为如下形式:
△ θ t = − α G t + ϵ ∗ g t △\theta_{t}=-\frac{\alpha}{\sqrt {G_{t}+\epsilon}} *g_{t} △θt=−Gt+ϵα∗gt
我们现在将其中的对角矩阵 G t G_{t} Gt用上述定义的基于过去梯度平方和的衰减均值 E [ g t 2 ] E[g^2_{t}] E[gt2]替换: △ θ t = − α E [ g 2 ] t + ϵ ∗ g t △\theta_{t}=-\frac{\alpha}{\sqrt {E[g^{2}]_{t}+\epsilon}} *g_{t} △θt=−E[g2]t+ϵα∗gt
因为分母表达式的形式与梯度值的均方根(root mean squared,RMS)**[在统计分析中将所有值平方求和,求其均值,在开平方得到的就是均方根]**形式类似,因而我们使用相应的简写来替换:
△ θ t = − α R M S [ g ] t g t △\theta_{t}=-\frac{\alpha}{RMS[g]_{t}} g_{t} △θt=−RMS[g]tαgt
其中在该更新中(在 SGD、动量法或者 Adagrad 也类似)的单位并不一致,也就是说,更新值的量级与参数值的假设量级并不一致。为改进这个问题,作者定义了另外一种指数衰减的衰减均值,他是基于参数更新的平方而非梯度的平方来定义的
E [ △ θ 2 ] t = γ E [ △ θ 2 ] t − 1 + ( 1 − γ ) △ θ t 2 E[△\theta^2]_{t} = \gamma E[△\theta^2]_{t-1}+(1-\gamma)△\theta^2_{t} E[△θ2]t=γE[△θ2]t−1+(1−γ)△θt2
因此,对该问题的均方根为:
R M S [ △ θ ] t = E [ △ θ 2 ] t + ϵ RMS[△\theta]_{t}=\sqrt{E[△\theta^2]_{t}+\epsilon} RMS[△θ]t=E[△θ2]t+ϵ
因为 R M S [ △ θ ] t RMS[△\theta]_{t} RMS[△θ]t值未知,所以我们用更新直到前一步的RMS的参数接近它。将前面更新规则中的 α \alpha α替换为 R M S [ △ θ ] t − 1 RMS[△\theta]_{t-1} RMS[△θ]t−1,我们最终得到了 Adadelta 法的更新规则:
△ θ t = − R M S [ △ θ ] t − 1 R M S [ g ] t g t △\theta_{t}=-\frac{RMS[△\theta]_{t-1}}{RMS[g]_{t}}g_{t} △θt=−RMS[g]tRMS[△θ]t−1gt θ t + 1 = θ + △ θ t \theta_{t+1}=\theta+△\theta_{t} θt+1=θ+△θt
借助 Adadelta 法,我们甚至不需要预设一个默认学习率,因为它已经从我们的更新规则中被删除了
RMSprop
RMSprop 是由 Geoff Hinton 在他 Coursera 课程中提出的一种适应性学习率方法,至今仍未被公开发表。
RMSprop 法和 Adadelta 法几乎同时被发展出来。他们是为了解决 Adagrad 中 α \alpha α快速缩减的问题。实际上,RMSprop 和我们推导出的 Adadelta 法第一个更规则相同,即使用指数加权平均消除在梯度下降过程中的振荡,假如某一维度的导数较大在指数加权平均大一些,否则小一些,这保证了各维度的导数在同一量级,较减少了振荡,允许使用一个更大的学习率。参数的更新公式如下所示:
E [ g 2 ] t = 0.9 E [ g 2 ] t − 1 + 0.1 g t 2 E[g^2]_{t}=0.9E[g^2]_{t-1}+0.1g^2_{t} E[g2]t=0.9E[g2]t−1+0.1gt2 θ t + 1 = θ t − α E [ g 2 ] t + ϵ g t \theta_{t+1}=\theta_{t}-\frac{\alpha}{\sqrt{E[g^2]_{t}+\epsilon}}g_{t} θt+1=θt−E[g2]t+ϵαgt
RMSprop 也将 α \alpha α除以了一个指数衰减的衰减均值。Hinton 建议设定 为 0.9,对 而言,0.001 是一个较好的默认值
Adam
它是另一种能对不同参数计算适应性学习率的方法。除了存储类似 Adadelta 法或 RMSprop 中过去梯度的平方 v t v_{t} vt的指数衰减平均值外,Adam 法也存储像动量法中的过去梯度 m t m_{t} mt的指数衰减平均值 ,更新公式如下:
m t = β m t − 1 + ( 1 − β 1 ) g t m_{t}=\beta m_{t-1}+(1-\beta_{1})g_{t} mt=βmt−1+(1−β1)gt v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 v_{t}=\beta_{2} v_{t-1}+(1-\beta_{2})g^2_{t} vt=β2vt−1+(1−β2)gt2
其中 m t m_{t} mt和 v t v_{t} vt分别是梯度的一阶矩(均值)和二阶矩(表示不确定度的方差),这也就是该方法名字的来源。因为当 m t m_{t} mt和 v t v_{t} vt一开始被初始化为 0 向量时,Adam 的作者观察到,该方法会有趋向 0 的偏差,尤其是在最初的几步或是在衰减率很小(即 β 1 \beta_{1} β1 和 β 2 \beta_{2} β2 接近 1)的情况下。所以他们使用偏差纠正系数,来修正一阶矩和二阶矩的偏差:
m ^ t = m t 1 − β 1 t \hat {m}_{t}=\frac{m_{t}}{1-\beta^t_{1}} m^t=1−β1tmt v ^ t = v t 1 − β 2 t \hat {v}_{t}=\frac{v_{t}}{1-\beta^t_{2}} v^t=1−β2tvt
他们使用这些来更新参数,更新规则很我们在 Adadelta 和 RMSprop 法中看到的一样,服从 Adam 的更新规则:
θ t + 1 = θ t − α v ^ t + ϵ m ^ t \theta_{t+1}=\theta_{t}-\frac{\alpha}{\sqrt{\hat{v}_{t}}+\epsilon}\hat{m}_{t} θt+1=θt−v^t+ϵαm^t
作者认为 β 1 \beta_{1} β1默认值0.9, β 2 \beta_{2} β2取默认值0.999, ϵ \epsilon ϵ取默认值 1 0 − 8 10^-8 10−8。他们的经验表明,Adam 在实践中和其他适应性学习算法相比表现要好。
各种改进算法的效果对比:
从中我们可以看出,Adagard、Adadelta、RMSprop可以很快的找到正确的方向,收敛速度相当快。

上图展示了不同的方法在鞍点处的情况,从中我们可以看出Adagard、Adadelta、RMSprop可以很快的逃离鞍点,其中Adadelta速度最快;NAG和Momentum虽然最终也可以逃离鞍点,但速度明显较慢,而SDG无法逃离。
动态图详见:An overview of gradient descent optimization algorithms
梯度下降法的限制
在很多优化问题中,梯度下降法都可以表现得很好,但是它并不是万能的,在某些方面它会存在一些挑战:
-
数据的挑战:当我们要解决的问题是凸优化问题时,我们可以得到一个最优值。但是当非凸优化问题时,很难使用梯度下降得到一个理想的结果。而且在凸优化问题中,我们最后得到的往往也只是局部的最优点
-
梯度的挑战:在神经网络中,可能会出现梯度消失或是梯度爆炸的问题,从而导致算法难以收敛
-
应用的挑战:比如在神经网络中使用梯度下降,我们就需要考虑它所占用的资源问题
使用梯度下降法的小提示
- 如果在训练一个很深或是很复杂的神经网络时想要快速收敛,则应该使用自适应方法,如Adam、Adagrad等。它们不需要太多超参数调优,就可以得到不错的结果
- 但为了得到最好的结果,你应该使用普通的梯度下降或动量梯度下降。虽然速度较慢,但这些结果大多优于自适应技术。
- 如果数据很小,并且可以在单个迭代中使用,那么可以使用诸如l-BFGS之类的二阶技术。因为二阶技术非常快速和准确,但只有当数据足够小时才可行
总的来说在大多数的问题中,Adam的效果都要普遍优于其他的方法。
参考
梯度下降(Gradient Descent)小结
最清晰的讲解各种梯度下降法原理与Dropout
一文简述深度学习优化方法-梯度下降
深度学习优化函数详解(4)-- momentum 动量法
An overview of gradient descent optimization algorithms
Gradient Descent
Gradient Descent is THE most used learning algorithm in Machine Learning and this post will show you almost everything you need to know about it.
Introduction to Gradient Descent Algorithm (along with variants) in Machine Learning

