如何理解生成模型和判别模型
Generative vs. Discriminative Models
直观上理解
如何理解生成模型和判别模型呢,我们以生活中的一个实例来看一下,我们如何来判断一个人所讲的语言呢?如果我们详细的学习了所有的语言的相关内容,当听到一个人所讲的语言时,就可以决定它是属于哪一种,这样的做法就是生成式方法;而如果我们并没有仔细的学习每一门语言,只是学习了如何区分不同语言的方法,这样的做法就是判别式方法。
从理论上理解
对于分类问题而言,机器学习的目标可以简单的理解为从一个给定的数据集上,学习一个从自变量(特征) X X X 到因变量(类标签) Y Y Y 的映射(函数)。
那么对于判别方法而言,它最后学习到的一个条件概率 P ( Y ∣ X ) P(Y|X) P(Y∣X) ;而生成模型学习到的是一个关于 X X X 和 Y Y Y 的联合概率 P ( Y , X ) = P ( Y ∣ X ) P ( X ) P(Y,X) = P(Y|X) P(X) P(Y,X)=P(Y∣X)P(X) ,然后我们可以通过贝叶斯定理计算条件概率 P ( Y ∣ X ) P(Y|X) P(Y∣X) 。
-
判别式方法:它关注的是寻找到一个关于 P ( Y ∣ X ) P(Y|X) P(Y∣X) 的好的拟合的超平面,而不管数据生成的过程,常见的算法有K近邻、SVMs、感知机等。例如在二分类问题中,我们的数据分布如下所示
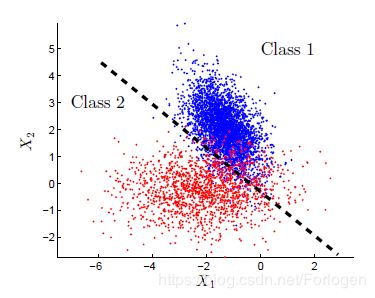
我们通过训练数据获得的分类器表现在二维图中就是上图黑色虚线代表的拟合边界,当我们有新的数据到来时,我们只需要看它落在虚线的哪一边:如果在红色的点一边,就判定它为第2类;如果落在蓝色点那一边,就判定为第1类。
对于判别式方法而言,我们所做的就是从所给的数据中计算出分类器中的某些未知参数,这样就得到了一个分类器,然后就可以使用它来预测新的样本的类别。因为它只在在训练数据上进行建模,所以得到的模型能力较差,容易发生过拟合。
-
生成式方法:它关注的是建立一个概率模型(联合概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X) ),显式地来看就是找到特征相应的类标签数据满足的分布模型。相比于判别式方法,它更关注的是数据的产生过程,常见的算法有朴素贝叶斯、隐马尔科夫模型等。例如所给的数据如下所示:
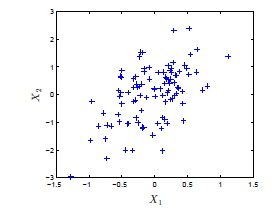
我们希望做的不是找到类似上面那样的分类边界,而是要找到它满足的类似下图的分布模型。
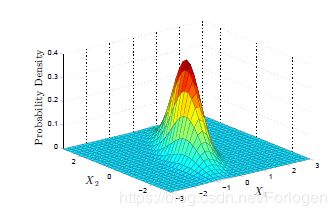
对于生成式方法而言,我们同样需要对所有的数据进行建模,这里的数据不只是所给的数据。希望通过它得到的模型可以来解释所有的数据,所以它的能力更强,而且更加灵活,可以处理各种任务,比如分类、回归等,甚至可以根据求出的模型生成新的数据。
求解模型参数
不管是生成式方法还是判别式方法,最后的模型我们都可以用含有某些参数的函数进行表示,而建模的过程其实也就是求解这些参数的过程。
假设我们的训练数据集为 D = ( X i ) , 1 = 1 , 2 , . . . , n D=(X_{i}),1=1,2,...,n D=(Xi),1=1,2,...,n ,其中 x i x_{i} xi 均满足独立同分布的采样于分布 P θ P_{\theta} Pθ ,那么我们的数据集就可以写成如下的形式
X i ∼ P θ , ( X 1 , X 2 , . . . , X n ) ∼ P θ ⨂ n X_{i} \sim P_{\theta},(X_{1},X_{2},...,X_{n})\sim P_{\theta}^{\bigotimes n} Xi∼Pθ,(X1,X2,...,Xn)∼Pθ⨂n
那么 p θ p_{\theta} pθ 是属于某一个概率分布族 P P P ,即
P = { P θ : θ ∈ Θ } P = \{ P_{\theta}:\theta \in \Theta\} P={Pθ:θ∈Θ}
我们要做的就是从 Θ \Theta Θ 中找到满足训练数据分布 P θ P_{\theta} Pθ 的参数 θ \theta θ 。那么具体可以使用什么方法求解呢?换言之,假设我们对训练数据所满足的模型一无所知,如何找到它所满足的模型呢?
其中一种方法便是使用极大似然估计,它的含义如下所示

通过求解似然函数的最大值,便可以得到最优的参数 θ ^ n ∗ \hat{\theta}_{n}^{*} θ^n∗。
所以根据训练数据可设它的似然函数为
L n ( θ , D ) = ∏ i = 1 n p θ ( X i ) L_{n}(\theta,D)=\prod_{i=1}^n p_{\theta}(X_{i}) Ln(θ,D)=i=1∏npθ(Xi)
求解 L n ( θ , n ) L_{n}(\theta,n) Ln(θ,n)就可以得到 θ n ∗ ^ \hat{\theta_{n}^{*}} θn∗^。根据理论证明,我们就可以将 θ n ∗ ^ \hat{\theta_{n}^{*}} θn∗^ 作为$\theta $ 的最优估计值。
如果我们知道数据采样于如下所示某个高斯模型
P θ ( X ) = 1 2 π σ e x p ( − ( X − μ ) 2 2 σ 2 ) P_{\theta}(X) = \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(X-\mu)^2}{2 \sigma^2}) Pθ(X)=2πσ1exp(−2σ2(X−μ)2)
那么 θ = ( μ , σ ) \theta = (\mu,\sigma) θ=(μ,σ)。对应的
Θ = { ( μ , σ ) : μ ∈ R , σ ∈ R + } \Theta =\{ (\mu,\sigma):\mu \in R,\sigma \in R^{+}\} Θ={(μ,σ):μ∈R,σ∈R+}
P = { 1 2 π σ e ( − ( X − μ ) 2 2 σ 2 ) : μ ∈ R , σ ∈ R + } P=\{\frac{1}{\sqrt{2\pi}\sigma}e(-\frac{(X-\mu)^2}{2 \sigma^2}):\mu \in R,\sigma \in R^{+}\} P={2πσ1e(−2σ2(X−μ)2):μ∈R,σ∈R+}
则似然函数为:
L n ( θ , D ) = ∏ i = 1 n 1 2 π σ e ( − ( X i − μ ) 2 2 σ 2 ) = ( 2 π σ ) − n g − 1 2 σ 2 ∑ i = 1 n ( X i − μ ) 2 L_{n}(\theta,D)=\prod_{i=1}^n\frac{1}{\sqrt{2\pi}\sigma}e(-\frac{(X_{i}-\mu)^2}{2 \sigma^2})=(\sqrt{2\pi}\sigma)^{-n}g^{\frac{-1}{2 \sigma^2}}\sum_{i=1}^n(X_{i}-\mu)^2 Ln(θ,D)=i=1∏n2πσ1e(−2σ2(Xi−μ)2)=(2πσ)−ng2σ2−1i=1∑n(Xi−μ)2
那么最优参数的求解表达式可表示为
( μ n ∗ ^ , σ n ∗ ^ ) = a r g max μ ∈ R , σ ∈ R + ( 2 π σ ) − n g − 1 2 σ 2 ∑ i = 1 n ( X i − μ ) 2 (\hat{\mu_{n}^{\ast}},\hat{\sigma_{n}^{\ast}})=arg\max \limits_{\mu \in R,\sigma \in R^{+}}(\sqrt{2\pi}\sigma)^{-n}g^{\frac{-1}{2 \sigma^2}}\sum_{i=1}^n(X_{i}-\mu)^2 (μn∗^,σn∗^)=argμ∈R,σ∈R+max(2πσ)−ng2σ2−1i=1∑n(Xi−μ)2
为了方便计算和为了避免似然函数中连乘可能造成下溢,常将其转换为log函数的形式
log ( L ( θ , D ) ) = − n 2 log ( 2 π σ 2 ) − 1 2 σ 2 ∑ i = 1 n ( X i − μ ) 2 \log(L(\theta,D))=\frac{-n}{2}\log(2\pi \sigma^2)-\frac{1}{2\sigma^2}\sum_{i=1}^n(X_{i}-\mu)^2 log(L(θ,D))=2−nlog(2πσ2)−2σ21i=1∑n(Xi−μ)2
因为上面的函数是单调的,所以对它求极大值等价于对最初的似然函数求极大值。下面我们对 θ \theta θ 求偏导,令其等于零。过程如下所示

这样便得到了最优的参数 μ n ∗ ^ , σ n ∗ ^ \hat{\mu_{n}^{\ast}},\hat{\sigma_{n}^{\ast}} μn∗^,σn∗^ 。
另外从Andrew Ng 的《On Discriminative vs. Generative classifier: A comparison of logistic regression and naive Bayes》中我们从更深的理论上来理解生成模型和判别模型,有兴趣的同学可以下载看一下。
作者把这两个模型用在各种数据集上面进行测试,最后得到在小数据上面Naive Bayes可以取得更好的效果,随着数据的增多、特征维度的增大,Logistic regression的效果更好。这也是因为Naive Bayes是生成模型,在有先验分布的情况下模型能够把数据拟合的更好,而Logistic regression属于生成模型,它不是去建模联合概率,通过训练数据直接预测输出,因此在数据足够多的情况下能够得到更好一些的效果。
总体上来说,一般认为判别式模型更受欢迎。最后作者作了较为全面的分析,产生式模型(Naive Bayes)在少量样本的情况下,可以取得更好的精确率,判别式模型(Logistic regression)在样本增加的情况下,逐渐逼近前者的概率。
而且在周志华的书中也讲到,基于有限的样本直接估计联合概率,在计算上会遭遇组合爆炸的问题,在数据上将会遭遇样本稀疏的问题,而且当属性越多的时候,问题越严重。在实际的问题中,我们可获取到的样本通常就是有限的,而且样本间还可能存在着类间不平衡的问题,因此很难使用这些有限的样本来估计得到一个接近真实分布的联合概率,这也是判别模型比生成模型更加流行的原因。
参考
https://blog.csdn.net/cjneo/article/details/45167223
https://blog.csdn.net/lanchunhui/article/details/60321358
http://lin-ml.blogspot.com/2017/05/generative-model-and-discriminative-model.html
https://taweihuang.hpd.io/2017/03/21/mlbayes/
http://blog.sina.com.cn/s/blog_6816fc2c0102v2hg.html
http://ai.stanford.edu/~ang/papers/nips01-discriminativegenerative.pdf