时间序列分析之ADF检验

ADF检验

在使用很多时间序列模型的时候，如 ARMA、ARIMA，都会要求时间序列是平稳的，所以一般在研究一段时间序列的时候，第一步都需要进行平稳性检验，除了用肉眼检测的方法，另外比较常用的严格的统计检验方法就是ADF检验，也叫做单位根检验。

ADF检验全称是 Augmented Dickey-Fuller test，顾名思义，ADF是 Dickey-Fuller检验的增广形式。DF检验只能应用于一阶情况，当序列存在高阶的滞后相关时，可以使用ADF检验，所以说ADF是对DF检验的扩展。

单位根（unit root）

在做ADF检验，也就是单位根检验时，需要先明白一个概念，也就是要检验的对象——单位根。

当一个自回归过程中： ，如果滞后项系数b为1，就称为单位根。当单位根存在时，自变量和因变量之间的关系具有欺骗性，因为残差序列的任何误差都不会随着样本量（即时期数）增大而衰减，也就是说模型中的残差的影响是永久的。这种回归又称作伪回归。如果单位根存在，这个过程就是一个随机漫步（random walk）。

ADF检验的原理

ADF检验就是判断序列是否存在单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根。

所以，ADF检验的 H0 假设就是存在单位根，如果得到的显著性检验统计量小于三个置信度（10%，5%，1%），则对应有（90%，95，99%）的把握来拒绝原假设。

ADF检验的python实现

ADF检验可以通过python中的 statsmodels 模块，这个模块提供了很多统计模型。

使用方法如下：

导入adfuller函数

from statsmodels.tsa.stattools import adfuller

adfuller函数的参数意义分别是：

1. x：一维的数据序列。
2. maxlag：最大滞后数目。
3. regression：回归中的包含项（c：只有常数项，默认；ct：常数项和趋势项；ctt：常数项，线性二次项；nc：没有常数项和趋势项）
4. autolag：自动选择滞后数目（AIC：赤池信息准则，默认；BIC：贝叶斯信息准则；t-stat：基于maxlag，从maxlag开始并删除一个滞后直到最后一个滞后长度基于 t-statistic 显著性小于5%为止；None：使用maxlag指定的滞后）
5. store：True  False，默认。
6. regresults：True 完整的回归结果将返回。False，默认。

返回值意义为：

1. adf：Test statistic，T检验，假设检验值。
2. pvalue：假设检验结果。
3. usedlag：使用的滞后阶数。
4. nobs：用于ADF回归和计算临界值用到的观测值数目。
5. icbest：如果autolag不是None的话，返回最大的信息准则值。
6. resstore：将结果合并为一个dummy。

def adfuller(x, maxlag=None, regression="c", autolag='AIC',
             store=False, regresults=False):
    """
    Augmented Dickey-Fuller unit root test

    The Augmented Dickey-Fuller test can be used to test for a unit root in a
    univariate process in the presence of serial correlation.

    Parameters
    ----------
    x : array_like, 1d
        data series
    maxlag : int
        Maximum lag which is included in test, default 12*(nobs/100)^{1/4}
    regression : {'c','ct','ctt','nc'}
        Constant and trend order to include in regression

        * 'c' : constant only (default)
        * 'ct' : constant and trend
        * 'ctt' : constant, and linear and quadratic trend
        * 'nc' : no constant, no trend
    autolag : {'AIC', 'BIC', 't-stat', None}
        * if None, then maxlag lags are used
        * if 'AIC' (default) or 'BIC', then the number of lags is chosen
          to minimize the corresponding information criterion
        * 't-stat' based choice of maxlag.  Starts with maxlag and drops a
          lag until the t-statistic on the last lag length is significant
          using a 5%-sized test
    store : bool
        If True, then a result instance is returned additionally to
        the adf statistic. Default is False
    regresults : bool, optional
        If True, the full regression results are returned. Default is False

    Returns
    -------
    adf : float
        Test statistic
    pvalue : float
        MacKinnon's approximate p-value based on MacKinnon (1994, 2010)
    usedlag : int
        Number of lags used
    nobs : int
        Number of observations used for the ADF regression and calculation of
        the critical values
    critical values : dict
        Critical values for the test statistic at the 1 %, 5 %, and 10 %
        levels. Based on MacKinnon (2010)
    icbest : float
        The maximized information criterion if autolag is not None.
    resstore : ResultStore, optional
        A dummy class with results attached as attributes
    """

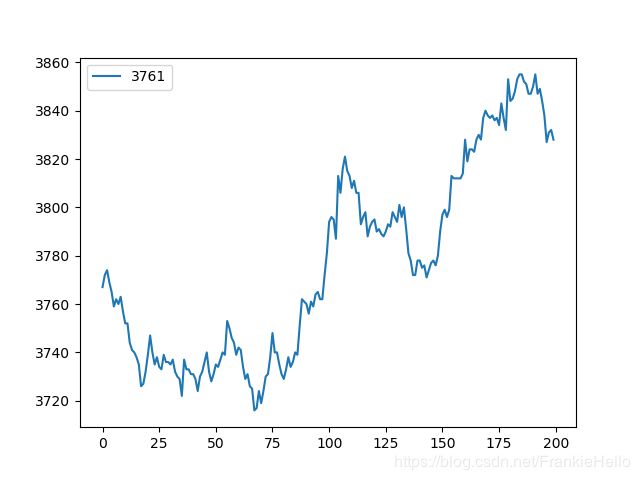
 现在我们用一个RB1309的收盘数据来进行ADF检验，看一下结果：

result = adfuller(rb_price)
print(result)


(-0.45153867687808574, 0.9011315454402649, 1, 198, {'5%': -2.876250632135043, '1%': -3.4638151713286316, '10%': -2.574611347821651}, 1172.4579344852016)

看到 t-statistic 的值 -0.451 要大于10%，所以无法拒绝原假设，另外，p-value的值也很大。

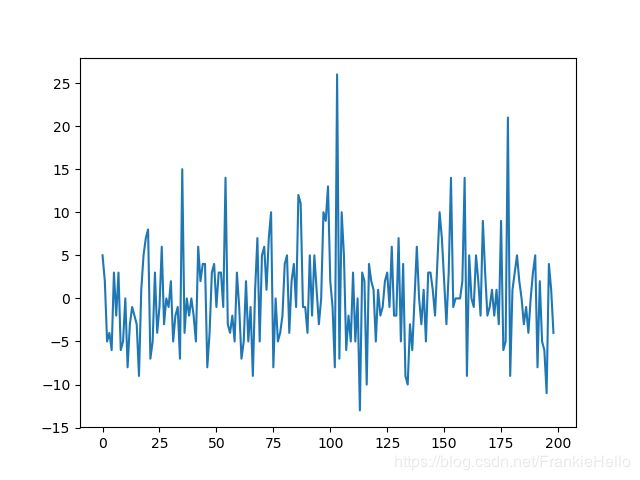
将数据进行一阶差分滞后，看一下结果如何：

rb_price = np.diff(rb_price)
result = adfuller(rb_price)
print(result)

(-15.436034211511204, 2.90628134201655e-28, 0, 198, {'5%': -2.876250632135043, '1%': -3.4638151713286316, '10%': -2.574611347821651}, 1165.1556545612445)

 看到 t-statistic 的值 -15 要小于5%，所以拒绝原假设，另外，p-value的值也很小。