统计套利之配对交易策略实现(基于python)
关于做统计套利所需要的基本知识在前面也整理过了:
时间序列分析之ADF检验
时间序列分析之协整检验
时间序列分析之相关性
下面用python实现一个简单的配对交易策略:
目录
一、交易对象选取
相关性检验
ADF检验
协整检验
二、主体策略
投资组合的构建
设置开仓和止损的阈值
三、历史回测
四、注意
一、交易对象选取
我们以商品期货市场的螺纹钢品种的跨期套利为例,选取两组不同到期月份的同种商品期货合约作为交易对象。
相关性检验
通过新浪财经的期货数据接口爬取螺纹钢rb1903到rb1908的六组数据,先看一下它们的走势:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import urllib.request as urllib2
import json
def findPairs():
ids = ['rb1903', 'rb1904', 'rb1905', 'rb1906', 'rb1907', 'rb1908']
url_5m = 'http://stock2.finance.sina.com.cn/futures/api/json.php/IndexService.getInnerFuturesMiniKLine5m?symbol='
result = []
for id in ids:
url = url_5m + id
req = urllib2.Request(url)
rsp = urllib2.urlopen(req)
res = rsp.read()
res_json = json.loads(res)
result.append(res_json)
close_result = []
for instrument in result:
oneDay_list = []
for oneDay in instrument:
oneDay_list.append(float(oneDay[-2]))
close_result.append(np.array(oneDay_list))
close_result = np.array(close_result)
close_result = close_result.T
df = pd.DataFrame(data=close_result, columns=ids)
df.plot()
plt.show()
从价格的走势图中,可以看出 rb1903 和 rb1904 以及 rb1908 和 rb1907 的走势上存在很强的相关性,下面画出它们之间的相关矩阵。
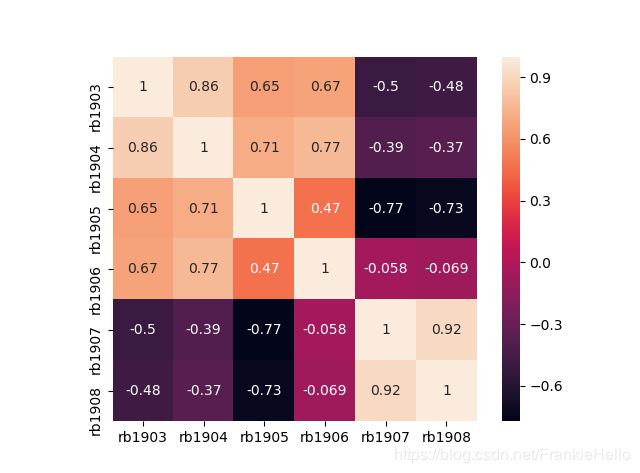
sns.heatmap(df.corr(), annot=True, square=True)
plt.show()
正如我们所推断的, rb1903 和 rb1904 以及 rb1908 和 rb1907这两组之间具有很强的相关性,其中,rb1907 和 rb1908 之间的相关程度最大,所以下面我们将选取 rb1907 和 rb1908作为配对交易的品种。
ADF检验
下面对这两组数据进行平稳性检验。
from statsmodels.tsa.stattools import adfuller
def check():
df = pd.read_csv('./data.csv')
price_A = df['rb1907'].values
price_B = df['rb1908'].values
result_A = adfuller(price_A)
result_B = adfuller(price_B)
print(result_A)
print(result_B)结果如下:
(-1.7605803524947852, 0.4002005032657946, 3, 238, {'1%': -3.458128284586202, '5%': -2.873761835239286, '10%': -2.5732834559706235}, 1750.3205777927317)
(-1.6918211072949225, 0.4353313388810546, 2, 239, {'1%': -3.458010773719797, '5%': -2.8737103617125186, '10%': -2.5732559963936206}, 1776.486392805771)从结果可以看出 t-statistic 的值要大于10%,所以说无法拒绝原假设,也就是原数据都是非平稳的。
下面进行一阶差分之后检查一下:
def check():
df = pd.read_csv('./data.csv')
price_A = df['rb1907'].values
price_B = df['rb1908'].values
price_A = np.diff(price_A)
price_B = np.diff(price_B)
result_A = adfuller(price_A)
result_B = adfuller(price_B)
print(result_A)
print(result_B)结果如下:
(-7.519664365222082, 3.820429924735319e-11, 2, 238, {'1%': -3.458128284586202, '5%': -2.873761835239286, '10%': -2.5732834559706235}, 1744.3991445433894)
(-9.917570016245815, 3.051148786023717e-17, 1, 239, {'1%': -3.458010773719797, '5%': -2.8737103617125186, '10%': -2.5732559963936206}, 1770.1154237195128)
结果可以看出,一阶差分之后的数据是平稳的,也就是说原数据是一阶单整的,满足协整关系的前提,所以下一步我们对这两组数据进行协整检验,来探究两者是否是协整的。
协整检验
from statsmodels.tsa.stattools import coint
def check():
df = pd.read_csv('./data.csv')
price_A = df['rb1907'].values
price_B = df['rb1908'].values
print(coint(price_A, price_B))(-3.6104387172088277, 0.02378223384906601, array([-3.94246081, -3.36160059, -3.06209517]))
结果看出 t-statistic 小于5%,所以说有95%的把握说两者具有协整关系。
二、主体策略
下面将构建配对交易的策略,统计套利的关键是要保证策略的市场中性,也就是说无论市场的趋势是上升还是下降,都要使策略或者预期的收益。
投资组合的构建
配对交易主要分析的对象是两个品种价格之间的偏离,由均值回归理论知,在股票、期货或者其他金融衍生品的交易市场中,无论高于或低于价值中枢(或均值)都有很高的概率向价值中枢回归的趋势。所以说,在具有协整关系的这两组数据中,当它们两者的价差高与均值时则会有向低走的趋势,价差低于均值时则会有向高走的趋势。
下面得到去中心化后的价差序列:
def strategy():
df = pd.read_csv('./data.csv')
price_A = df['rb1907'].values
price_B = df['rb1908'].values
spread = price_A - price_B
mspread = spread - np.mean(spread)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(len(mspread)), mspread)
ax.hlines(0, 0, len(mspread))
plt.show()
注意这里直接研究的是 A、B 价格差值,统计套利策略中通常会将 B 价格乘以一个协整系数,研究的对象是它们的残差,由于协整检验后可以知道它们的残差具有平稳性,所以更好的应用均值回归的理论。
设置开仓和止损的阈值
为了使开仓和止损的阈值更好地比较,所以就将开仓阈值设置为窗口内数据的两倍标准差,止损设置为三倍标准差。这个标准差的倍数可以通过调参来不断调优,标准差的设置也可以通过 GARCH 等模型拟合的自回归条件异方差类似的时变标准差来代替。
def strategy():
df = pd.read_csv('./data.csv')
price_A = df['rb1907'].values
price_B = df['rb1908'].values
spread = price_A - price_B
mspread = spread - np.mean(spread)
sigma = np.std(mspread)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(len(mspread)), mspread)
ax.hlines(0, 0, len(mspread))
ax.hlines(2 * sigma, 0, len(mspread), colors='b')
ax.hlines(-2 * sigma, 0, len(mspread), colors='b')
ax.hlines(3 * sigma, 0, len(mspread), colors='r')
ax.hlines(-3 * sigma, 0, len(mspread), colors='r')
plt.show()
三、历史回测
下面就以样本内数据进行回测一下:
def strategy():
df = pd.read_csv('./data.csv')
price_A = df['rb1907'].values
price_B = df['rb1908'].values
spread = price_A - price_B
mspread = spread - np.mean(spread)
sigma = np.std(mspread)
open = 2 * sigma
stop = 3 * sigma
profit_list = []
hold = False
hold_price_A = 0
hold_price_B = 0
hold_state = 0 # 1 (A:long B:short) -1 (A:short B:long)
profit = 0
for i in range(len(price_A)):
if hold == False:
if mspread[i] >= open:
hold_price_A = price_A[i]
hold_price_B = price_B[i]
hold_state = -1
hold = True
elif mspread[i] <= -open:
hold_price_A = price_A[i]
hold_price_B = price_B[i]
hold_state = 1
hold = True
else:
if mspread[i] >= stop and hold_state == -1 :
profit = (hold_price_A - price_A[i]) + (price_B[i] - hold_price_B)
hold_state = 0
hold = False
if mspread[i] <= -stop and hold_state == 1 :
profit = (price_A[i] - hold_price_A) + (hold_price_B - price_B[i])
hold_state = 0
hold = False
if mspread[i] <= 0 and hold_state == -1:
profit = (hold_price_A - price_A[i]) + (price_B[i] - hold_price_B)
hold_state = 0
hold = False
if mspread[i] >= 0 and hold_state == 1:
profit = (price_A[i] - hold_price_A) + (hold_price_B - price_B[i])
hold_state = 0
hold = False
profit_list.append(profit)
print(profit_list)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(len(profit_list)), profit_list)
plt.show()
收益结果如下:
可以看出回测结果是很不尽人意的,因为我们并没有对参数进行调优,从前面可以知道统计套利单次的收益是比较薄弱的,主要原因不仅仅是价差带来的这种相对收益本来就比较低,还有就是止损阈值设置的问题,有时一次止损就会 cover 掉之前所有的收益。所以说在统计套利中,阈值的设置是非常重要的。
四、注意
1、为了方便操作,以上实验的策略构建以及历史回测都是样本内进行测试的,真正的策略回测要划分训练数据和测试数据,进行样本外测试。
2、在选择配对数据的品种时,除了要考虑配对品种的相关性之外,还要考虑品种的市场流动性等因素。
3、历史回测时,还需要将手续费、滑点等因素考虑进去。