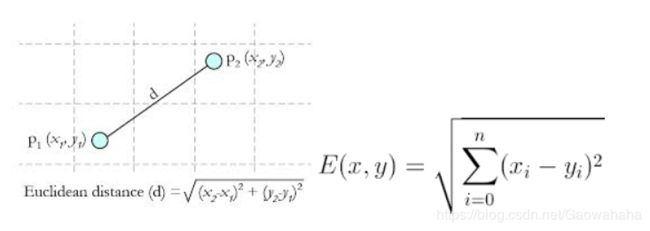算法二、K-近邻(KNN)算法
1、k-近邻法简介
k近邻法(k-nearest neighbor, k-NN)是1967年由Cover T和Hart P提出的一种基本分类与回归方法。它的工作原理是:存在一个样本数据集合,也称作为训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一个数据与所属分类的对应关系。输入没有标签的新数据后,将新的数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本最相似数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
举个简单的例子,我们可以使用k-近邻算法分类一个电影是爱情片还是动作片。
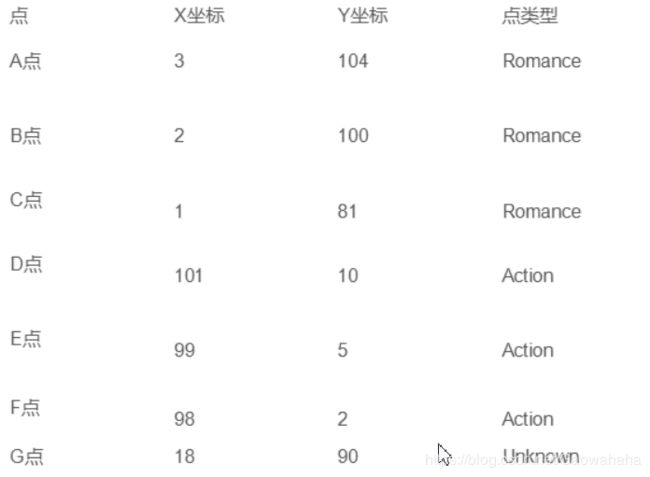
如上图所示就是我们已有的数据集合。这个数据集有两个特征,即打斗次数和接吻次数。同时我们也知道电影的分了标签即是爱情片还是动作片。我们将打斗次数和接吻次数转为X轴的坐标和Y轴的坐标。为了判断未知电影的类别,我们以所有已知电影的类别作为参照, 计算未知实例与所有已知实例的距离,然后根据距离的远近排序,选择最近K个已知的实例进行投票, 根据少数服从多数的投票法则(majority-voting),让未知实例归类为K个最邻近样本中最多数的类别(就是归为这K个实例中最多的那一类)。
关于距离的衡量方法:
3.2.1 Euclidean Distance 定义
其他距离衡量:余弦值(cos), 相关度 (correlation), 曼哈顿距离 (Manhattan distance)
通过计算,我们可以得到如下结果:
- (18,90)->爱情片(3,104)的距离约为20.51828453
- (18,90)->爱情片(2,100)的距离约为18.86796226
- (18,90)->爱情片(1,81)的距离约为19.23538406
- (18,90)->动作片(101,10)的距离约为115.27792503
- (18,90)->动作片(99,5)的距离约为117.41379817
- (18,90)->动作片(98,2)的距离约为118.92854998
- 假设去k为4,则最近的4个点钟有三个为爱情片,一个为动作片。所以未知类型的电影应该为爱情片!
# -*- coding: UTF-8 -*-
import numpy as np
import operator
"""
函数说明:计算给定数据集的经验熵(香农熵)
Parameters:
dataSet - 数据集
Returns:
shannonEnt - 经验熵(香农熵)
Author:
Aaron Gao
Modify:
2018-12-01
"""
def createData():
dataset=[[3,104,'爱情片'],
[2,100,'爱情片'],
[1,81,'爱情片'],
[101,10,'动作片'],
[99,5,'动作片'],
[98,2,'动作片']]
dataset=np.array(dataset)
labelList=dataset[:,-1]
featureList=dataset[:,:2]
return featureList,labelList
"""
函数说明:kNN算法,分类器
Parameters:
inX - 用于分类的数据(测试集)
dataSet - 用于训练的数据(训练集)
labes - 分类标签
k - kNN算法参数,选择距离最小的k个点
Returns:
sortedClassCount[0][0] - 分类结果
Modify:
2018-12-02
"""
def classify0(textData, dataSet, labels, k):
#numpy函数shape[0]返回dataSet的行数
dataSetSize = dataSet.shape[0]
#在列向量方向上重复textData共1次(横向),行向量方向上重复textData共dataSetSize次(纵向)
testDataList= np.tile(textData, (dataSetSize, 1))
#print(testDataList.dtype)
#print(dataSet.dtype)
dataSet=dataSet.astype('float64') #转换类型
diffMat =testDataList-dataSet
#print(diffMat)
#二维特征相减后平方
sqDiffMat = diffMat**2
#sum()所有元素相加,sum(0)列相加,sum(1)行相加
sqDistances = sqDiffMat.sum(axis=1)
#开方,计算出距离
distances = sqDistances**0.5
print(distances)
#返回distances中元素从小到大排序后的索引值
sortedDistIndices = distances.argsort()
#定一个记录类别次数的字典
classCount = {}
for i in range(k):
#取出前k个元素的类别
voteIlabel = labels[sortedDistIndices[i]]
#dict.get(key,default=None),字典的get()方法,返回指定键的值,如果值不在字典中返回默认值。
#计算类别次数
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
#python3中用items()替换python2中的iteritems()
#key=operator.itemgetter(1)根据字典的值进行排序
#key=operator.itemgetter(0)根据字典的键进行排序
print(classCount)
# reverse降序排序字典
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
#返回次数最多的类别,即所要分类的类别
return sortedClassCount[0][0]
if __name__=="__main__":
featureList,labelList=createData()
test=[18,90]
currLablel=classify0(test,featureList,labelList,4)
print('电影类型:'+str(currLablel))算法优缺点:
算法优点
简单
易于理解
容易实现
通过对K的选择可具备丢噪音数据的健壮性
算法缺点
需要大量空间储存所有已知实例
算法复杂度高(需要比较所有已知实例与要分类的实例)
当其样本分布不平衡时,比如其中一类样本过大(实例数量过多)占主导的时候,新的未知实例容易被归类为这个主导样本,因为这类样本实例的数量过大,但这个新的未知实例实际并木接近目标样本