CMU15 445/645课程-Tree Based Indexes笔记
B+Tree
一种搜索，插入，删除都是log(n)的数据结构
a.节点可以有超过两个的子节点
b.适合顺序存取
两种访问叶子节点值得方法
1.Record IDs:指针指向元祖位置
2.Tuple Data:远足内容存在叶子节点中
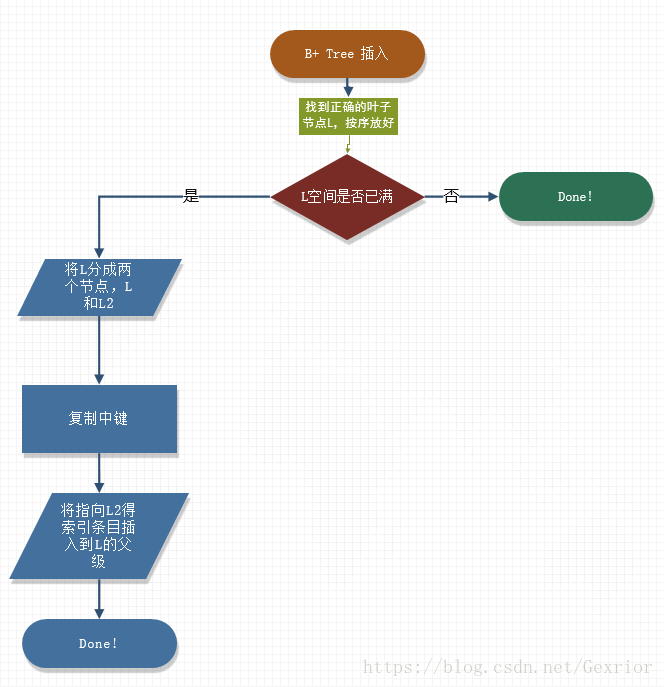
B+ Tree Operations
插入
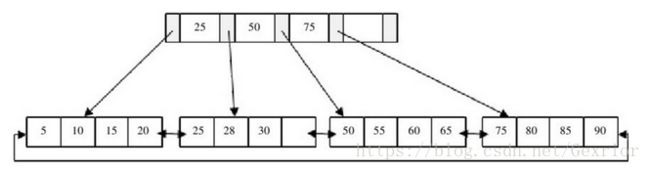
这时我们插入70
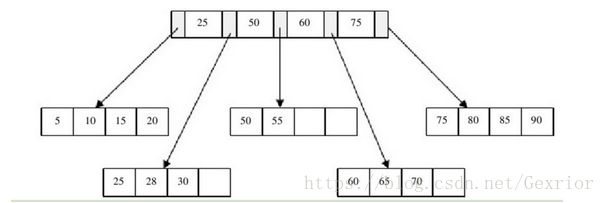
删除
首先，删除键值为70的这条记录，删除后。
接着我们删除键值为25的记录，但是该值还是Index Page中的值，因此在删除Leaf Page中25的值后，还应将25的右兄弟节点的28更新到Page Index中，最后可得到图。
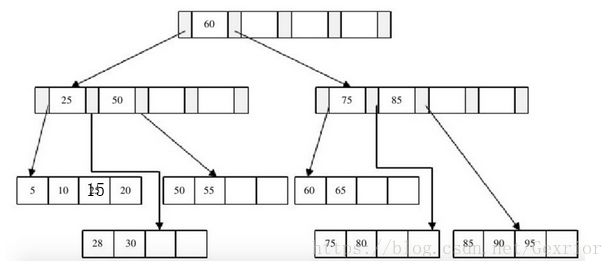
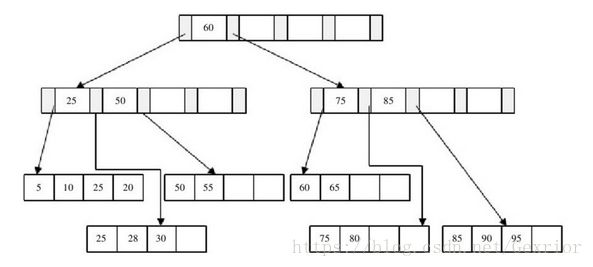
最后我们来看删除键值为60的情况，删除Leaf Page中键值为60的记录后，填充因子小于50%，这时需要做合并操作，同样，在删除Index Page中相关记录后需要做Index Page的合并操作，最后得到图。
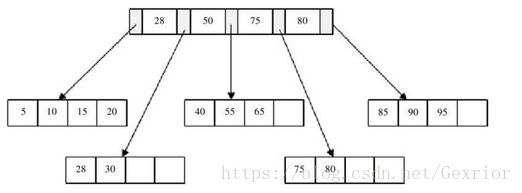
B+Tree 设计准测
Merge:
1.当DBMS半满时不会总是merge
2.延迟的merge操作会减少重组的数量
有重复键的索引
1.Duplicate keys:使用同一个叶子节点，但是存储相同的keys很多次
2.Value lists:只存储一次key，维护一个独一值的链表
不同长度的keys:
1.指针：存储键值作为指向元组属性的键值
2.不同长度的节点：B+tree的每个节点大小不同，但是需要仔细的内存管理
3.Key Map:插入一个指针数组，映射到节点中的key-value
前缀压缩：
1.中间层节点，我们不需要整个key
2.存储一个最小的节点，你要保证正确的指向索引
Skip List:
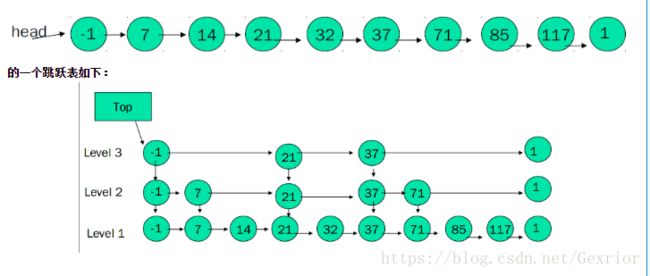
插入：扔硬币决定该节点在第几层，然后插入
删除：每个节点有一个flag，要删除时，就设置flag，告诉进程忽略这个值，然后一层一侧把他的引用给忽略点
Advantage over B+ Tree:
a.使用更少的内存
b.插入和删除不需要再次平衡
Disadvantage over B+ Tree:
a.硬盘/缓存不友好，因为没有优化位置
b.调用随机数（实现抛硬币）多次非常慢
Radix Tree:
1.每个字母一个节点，不同于TRIE（同样字母为一个节点，剩下的全部为一个节点）