机器学习总结之----2.逻辑回归

我也只是在学习的过程中，相当于自己理解推导一遍做个笔记，参考了别人很多东西，文末有相关链接。

什么是逻辑回归

逻辑回归也叫做对数几率回归，但它却用来做二分类。
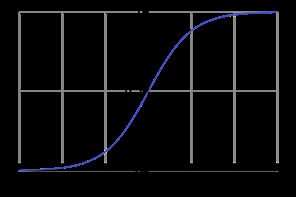
线性回归产生的预测值为 $z={\theta }^{T}x$，线性回归通常用来做回归。但是可以在线性回归基础上，加上性质像阶跃函数但光滑可导的sigmod函数，然后算出一个概率$p$来。如果$p$大于0.5，可以将它判定为一类（比如正例1），小于等于0.5判定为另一类（比如负例0）。

其中，sigmod函数（简写为$\sigma$）为：
$$\sigma (z)=\frac{1}{1+e^{-z}}$$

逻辑回归，在我看来就是线进行线性回归，再在它的基础上加上sigmod函数，得到一个概率值，进而判断该样本属于哪一类。计算公式如下：
$$p=\sigma (z)=\sigma ({\theta }^T\cdot x)=h_{\theta }(x)$$
其中，$\theta$是权重，也是我们待求参数。
根据概率值$p$对样本进行分类：
$$y=\{\begin{array}{cc}0& p<0.5,\\ 1& p\ge 0.5\end{array}$$

逻辑回归的代价函数

为了使正样本得到高的概率值$p$（接近1好），负样本得到低的概率值$p$（接近0好），从而找出权重参数$\theta$。设计单个样本的损失函数如下：
$$c(\theta )=\{\begin{array}{cc}-log(p)& y=1,\\ -log(1-p)& y=0\end{array}$$
对于整个数据集m个样本的损失函数如下：
$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}log(p^{(i)})+(1-y^{(i)})log(1-p^{(i)})]$$
虽然没有bishijie封闭解，但因为$J(\theta )$是凸函数，可以用梯度下降法求解。

极大似然估计

由以上公式，可知任何一个样本都有：
$$\{\begin{array}{c}P(y=1|x;\theta )=h_{\theta }(x)\\ P(y=0|x;\theta )=1-h_{\theta }(x)\end{array}$$

整合一下：
$$P(y|x;\theta )=h_{\theta }(x{)}^y(1-h_{\theta }(x){)}^{1-y}$$

那么，对于所有m个样本发生的概率是：
$$L(\theta )=\prod _{i=1}^{m}P(y^{(i)}|x^{(i)};\theta )=\prod _{i=1}^m{h}_{\theta }(x^{(i)}{)}^{y^{(i)}}(1-h_{\theta }(x^{(i)}){)}^{1-y^{(i)}}$$

取对数：
$$l(\theta )=logL(\theta )=\sum _{i=1}^m[y^{(i)}log{h}_{\theta }(x^{(i)})+(1-y^{(i)})(1-h_{\theta }(x^{(i)}))]$$

得到的结果实质上和损失函数是一样的。

利用梯度下降法求参数

sigmod函数有如下性质：
$$f^{{}^{\prime }}(x)=f(x)(1-f(x))$$
$J(\theta )$对$\theta$的第j个属性 求梯度，

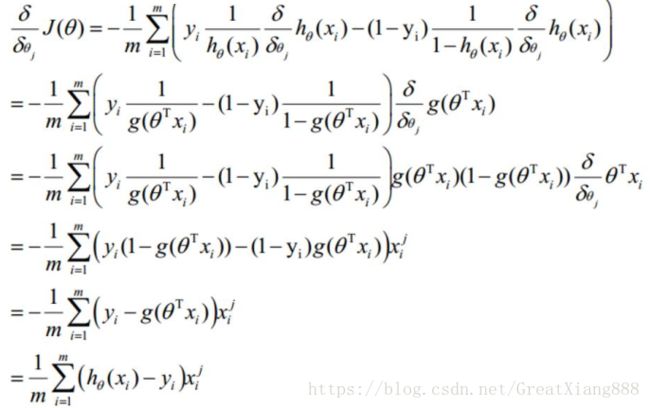
（公式实在太多了。。copy了一下）
图片中，下标i表示第i个样本，上标j表示第j维属性。（图片上下标和其他的文字刚好反过来）

最后，对$\theta$的第j个属性来说，梯度下降的表达式为：
$${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$

其中，$\alpha$是学习率，m为样本数量，$x^{(i)}$为第i个样本，是一个列向量，$h_{\theta }(x^{(i)})$是根据这个样本求得的预测概率值，$y^{(i)}$是样本的真实标签，$x_j^{(i)}$是第i个样本的第j个分量。

参考链接：
逻辑回归(logistic regression)的本质——极大似然估计
逻辑回归-爖 (很多精炼的数学推导，值得学习)
周志华. 机器学习 - 清华大学出版社, 2016