再谈数据结构(一):栈和队列
1 - 前言
栈和队列是两种非常常用的两种数据结构,它们的逻辑结构是线性的,存储结构有顺序存储和链式存储。在平时的学习中,感觉虽然栈和队列的概念十分容易理解,但是对于这两种数据结构的灵活运用及代码实现还是比较生疏。需要结合实际问题来熟练队列和栈的操作。
2 - 例题分析
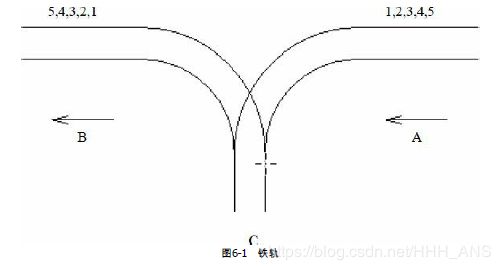
2.1 - 铁轨(Rails, ACM/ICPC CERC 1997, UVa 514)
某城市有一个火车站,铁轨铺设如图6-1所示。有n节车厢从A方向驶入车站,按进站顺
序编号为1~n。你的任务是判断是否能让它们按照某种特定的顺序进入B方向的铁轨并驶出
车站。例如,出栈顺序(5 4 1 2 3)是不可能的,但(5 4 3 2 1)是可能的。
Sample Input
5
1 2 3 4 5
5 4 1 2 3
0
6
6 5 4 3 2 1
0
0
Sample Output
Yes
No
为了重组车厢,你可以借助中转站C。这是一个可以停放任意多节车厢的车站,但由于
末端封顶,驶入C的车厢必须按照相反的顺序驶出C。对于每个车厢,一旦从A移入C,就不
能再回到A了;一旦从C移入B,就不能回到C了。换句话说,在任意时刻,只有两种选择:
A→C和C→B。
涉及知识及算法:
把station看做是一个栈,按1~N的顺序,先入栈一个车厢,如果栈顶的车厢编号和所给出的编号一样。那么火车就出栈,循环直到栈里边所有满足出站顺序的火车都出站或栈空,否则就入栈。最后判断所有火车是否都出站了。若都出站,输出Yes,否则输出No。
#include
#include //使用栈所需要引用的头文件
#include //让c++可以使用c的输入输出的操作。
#include
#include
using namespace std;
const int MAXN = 1010;
int n,target[MAXN];
int main()
{
while(scanf("%d",&n)==1){
stack s; //定义一个栈为s
int A = 1,B = 1;
for(int i=1;i<=n;i++)
scanf("%d",&target[i]);
int ok = 1;
while(B<=n){
if(A == target[B]){A++;B++;} //如果入栈元素A与target元素一致则直接输出,A+1,B+1
else if(!s.empty()&&s.top()==target[B]){s.pop();B++;} //如果栈s不为空且栈顶元素与target元素一致,则输出。B++
else if(A<=n) s.push(A++); //如果入栈元素A与target元素不一直且栈顶元素与target元素不一致,入栈,A++
else {ok = 0;break;} //循环到最后还有元素剩余则ok=0;
}
printf("%s\n",ok? "yes":"no");
}
return 0;
}
在C++中,可以使用关于栈的头文件:
#include
并且支持相应的栈的基本操作
定义stack 对象的示例代码如下:
stack
stack
stack 的基本操作有:
- 入栈,如例:s.push(x);
- 出栈,如例:s.pop();注意,出栈操作只是删除栈顶元素,并不返回该元素。
- 访问栈顶,如例:s.top()
- 判断栈空,如例:s.empty(),当栈空时,返回true。
- 访问栈中的元素个数,如例:s.size()。
具体基本操作实现代码:
让我们用更加底层的代码来实现栈的这些基本操作(要在C++的编译环境中实现此代码,因为Status InitStack(SqStack &S);使用了c++的引用语法)
- 顺序栈:
#include
#include
//--------------------栈的顺序存储结构--------------------
#define STACK_INIT_SIZE 100
#define STACKINCREACE 10
typedef char Elemtype;//在头文件中说明
typedef int Status;
typedef struct{
Elemtype *base;
Elemtype *top;
int stacksize;
}SqStack;
//----------------------函数声明部分----------------------
Status InitStack(SqStack &S);
Status Push(SqStack &S,Elemtype e);
Status Pop(SqStack &S,Elemtype &e);
Status GetTop(SqStack S,Elemtype &e);
Status StackEmpty(SqStack S);
Status ClearStack(SqStack &S);
Status DestroyStack(SqStack &S);
//--------------------主函数入口--------------------
int main(){
SqStack s1;
char getElem=NULL;
char popElem=NULL;
int empty_Flag=NULL;
InitStack(s1);
Push(s1,'a');
Push(s1,'b'); //压栈2个元素,当前栈中的元素为a,b
GetTop(s1,getElem);
printf("栈顶元素是:%c\n",getElem);
Pop(s1,popElem);
printf("出栈的元素是:%c\n",popElem);
GetTop(s1,getElem);
printf("栈顶元素是:%c\n",getElem);
if(StackEmpty(s1))
{
printf("空栈");
}
else printf("不为空栈\n");
Pop(s1,popElem);
printf("出栈的元素是:%c\n",popElem);
if(StackEmpty(s1))
{
printf("空栈");
}
else printf("不为空栈\n");
ClearStack(s1);
DestroyStack(s1);
return 0;
// printf("栈的长度:%d\n",StackLength(stack));
}
//------------------栈的初始化函数------------------
Status InitStack(SqStack &S){
S.base = (Elemtype *)malloc(STACK_INIT_SIZE*sizeof(Elemtype));
//2016.4.17编译时报错:missing “)”before ;
//错误原因:由于头文件中定义常量时后面加了;导致编译的时候将STACK_INIT_SIZE用100;代替,
//使得该函数提前结束语100处,malloc后的“(”找不到匹配的“)”而报错
//解决方法:去掉常量定义中的;
if(!S.base){
return false;
}
S.stacksize=STACK_INIT_SIZE;
S.top=S.base;
return true;
}
//---------------------入栈函数---------------------
Status Push(SqStack &S,Elemtype e){
//判断是否溢出
if(S.top-S.base>=S.stacksize){
S.base=(Elemtype *)realloc(S.base,(S.stacksize+STACKINCREACE)*sizeof(Elemtype));
if(!S.base){
return false;
}
S.top=S.base+S.stacksize;//注意因为这里的栈底指针的改变,导致栈顶指针随之改变
S.stacksize+=STACKINCREACE;
}
//压栈部分
*S.top=e;
S.top++;
return true;
}
//---------------------出栈函数---------------------
Status Pop(SqStack &S,Elemtype &e){
//非法判断
if(S.base==S.top){
return false;
}
S.top--; //注意这里因为top指向栈中当前元素的上一个空间,所以要先将其位置减一
e=*S.top;
return true;
}
//-------------------查看栈顶元素-------------------
Status GetTop(SqStack S,Elemtype &e){
if(S.base==S.top ){
return false;
}
e=*(S.top-1);
return true;
}
//------------------判断栈是否为空------------------
Status StackEmpty(SqStack S){
if(S.base==S.top){
return true;
}
return false;
}
//--------------------清空栈------------------------
Status ClearStack(SqStack &S){//清空栈的时候不用将stacksize重新赋值
S.top=S.base; //因为经过realloc函数重新分配空间后(stacksize大小改变),
return true; //S.base指向的是一段stacksize大小的连续存储空间
//即使将他重置,剩余的空间也是闲置的(顺序表里也只是经当前长度置为0)
}
//--------------------销毁栈------------------------
Status DestroyStack(SqStack &S){
free(S.base);
free(S.top);
S.base=NULL;
return true;
}
- 链式栈的基本操作
#include
#include
#define OK 1
#define ERROR 0
typedef int SElemType ;
typedef struct SNode{
SElemType data;
struct SNode *next;
}StackNode,*LinkStack;
//初始化
void Init_Stack_L(LinkStack L){
L=(StackNode*)malloc(sizeof(StackNode));
L->next=NULL;
}
//Push:入栈
int Push(LinkStack &L,SElemType e){
LinkStack p;
p=(StackNode*)malloc(sizeof(StackNode));
if(p==NULL) return ERROR;
p->data=e;
p->next=L;
L=p;
return OK;
}
int Pop(LinkStack &L,SElemType &e)
{
LinkStack p=L;
L=p->next;
e=p->data;
free(p);
return OK;
}
/*void Print(LinkStack &L) {
int e;
LinkStack p=L;
while(p)
{
printf("%3d",p->data);
p=p->next;
}
printf("\n");
}*/
int main()
{
LinkStack L;
int e;
Init_Stack_L(L);
Push(L,1);
Push(L,2);
Push(L,3);
Pop(L,e);
printf("%d\n",e);
Pop(L,e);
printf("%d\n",e);
return 0;
}
2-2 矩阵链乘(Matrix Chain Multiplication, UVa 442)
输入n个矩阵的维度和一些矩阵链乘表达式,输出乘法的次数。如果乘法无法进行,输
出error。假定A是mn矩阵,B是np矩阵,那么AB是mp矩阵,乘法次数为mnp。如果A的
列数不等于B的行数,则乘法无法进行。
例如,A是5010的,B是1020的,C是205的,则(A(BC))的乘法次数为10205(BC的
乘法次数)+ 50105((A(BC))的乘法次数)= 3500。
Sample Input
9
A 50 10
B 10 20
C 20 5
D 30 35
E 35 15
F 15 5
G 5 10
H 10 20
I 20 25
A
B
C
(AA)
(AB)
(AC)
(A(BC))
((AB)C)
(((((DE)F)G)H)I)
(D(E(F(G(HI)))))
((D(EF))((GH)I))
Sample Output
0
0
0
error
10000
error
3500
15000
40500
47500
15125
涉及知识及算法:
栈对于表达式求值有着特殊的作用。
本题的关键是解析表达式。本题的表达式比较简单,可以用一个栈来完成:遇到字母时
入栈,遇到右括号时出栈并计算,然后结果入栈。因为输入保证合法,括号无须入栈。
#include
#include //使用栈所需要引用的头文件
#include //让c++可以使用c的输入输出的操作。
#include
#include
using namespace std;
struct Matrix{
int a,b;
Matrix(int a=0, int b=0):a(a),b(b){} //赋缺省值a=0,b=0;
}m[26]; //构造一个矩阵的结构体
stacks; //初始化一个结构体的栈
int main()
{
int n;
cin>>n;
for(int i=0;i> name;
int k = name[0]-'A';
cin >> m[k].a>>m[k].b;
}
string expr;
while(cin>>expr)
{
int len = expr.length();
bool error = false;
int ans = 0;
for(int i = 0; i 2.3 - 团体队列(Team Queue,UVa540)
有t个团队的人正在排一个长队。每次新来一个人时,如果他有队友在排队,那么这个
新人会插队到最后一个队友的身后。如果没有任何一个队友排队,则他会排到长队的队尾。
输入每个团队中所有队员的编号,要求支持如下3种指令(前两种指令可以穿插进
行)。
- ENQUEUEx:编号为x的人进入长队。
- DEQUEUE:长队的队首出队。
- STOP:停止模拟。
对于每个DEQUEUE指令,输出出队的人的编号。
Sample Input
2
3 101 102 103
3 201 202 203
ENQUEUE 101
ENQUEUE 201
ENQUEUE
102
ENQUEUE 202
ENQUEUE 103
ENQUEUE
203
DEQUEUE
DEQUEUE
DEQUEUE
DEQUEUE
DEQUEUE
DEQUEUE
STOP
2
5
259001 259002 259003 259004 259005
6 260001 260002 260003 260004 260005
260006
ENQUEUE 259001
ENQUEUE 260001
ENQUEUE 259002
ENQUEUE
259003
ENQUEUE 259004
ENQUEUE 259005
DEQUEUE
DEQUEUE
ENQUEUE
260002
ENQUEUE
260003
DEQUEUE
DEQUEUE
DEQUEUE
DEQUEUE
STOP
0
Sample Output
Scenario
#1
101
102
103
201
202
203
Scenario
#2
259001
259002
259003
259004
259005
260001
【分析】
本题有两个队列:每个团队有一个队列,而团队整体又形成一个队列。例如,有3个团
队1,2,3,队员集合分别为{101,102,103,104}、{201,202}和{301,302,303},当前
长队为{301,303,103,101,102,201},则3个团队的队列分别为{103,101,102}、
{201}和{301,303},团队整体的队列为{3,1,2}。代码如下:
#include
#include
#include 在c++中使用队列的头文件
#include
相关队列的基本操作:
-
push()会将一个元素置入queue中。
-
front()会返回queue内的第一个元素(也就是第一个被置入的元素)。
-
back()会返回queue中最后一个元素(也就是最后被插入的元素)。
-
top()取队首元素(但不删除)。
-
pop()会从queue中移除一个元素。
注意:pop()虽然会移除下一个元素,但是并不返回它,front()和back()返回下一个元素但并不移除该元素。
队列的基本操作底层具体实现
- 顺序队列
#include "stdio.h"
#include "stdlib.h"
#include "io.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 11 //初始容量
typedef int Status;
typedef int QElemType;//定义数据类型
//循环队列的顺序存储结构
typedef struct{
QElemType data[MAXSIZE];
int front; //头指针
int rear;//尾指针,队列非空时,指向队尾元素的下一个位置
}SqQueue;
Status visit(QElemType item){
printf("%d",item);
return OK;
}
//初始化空队列
Status InitQueue(SqQueue *sQ){
sQ->front =0;
sQ->rear =0;
return OK;
}
//将队列清空
Status ClearQueue(SqQueue *Q){
Q->front = Q->rear =0;
return OK;
}
//判断队列是否为null
Status QueueEmpty(SqQueue Q){
if(Q.front == Q.rear)
return TRUE;
else
return FALSE;
}
//返回队列中的元素个数
int QueueLength(SqQueue Q){
return (Q.rear-Q.front+MAXSIZE)%MAXSIZE;
}
//返回队头元素
Status GetHead(SqQueue Q, QElemType *e){
if(Q.front == Q.rear)//是否为空队列
return ERROR;
*e = Q.data[Q.front];
return OK;
}
//在队尾插入元素
Status EnQueue(SqQueue *Q, QElemType e){
if((Q->rear+1)%MAXSIZE == Q->front)//队列已满
return ERROR;
Q->data[Q->rear] =e;//插入队尾
Q->rear = (Q->rear +1)%MAXSIZE;//尾部指针后移,如果到最后则转到头部
return OK;
}
//元素出队
Status DeQueue(SqQueue *Q, QElemType *e){
if(Q->front == Q->rear)//队列空
return ERROR;
*e = Q->data[Q->front];//返回队头元素
Q->front = (Q->front+1)%MAXSIZE;//队头指针后移,如到最后转到头部
return OK;
}
//遍历队列元素
Status QueueTraverse(SqQueue Q){
int i = Q.front;
while((i+Q.front) != Q.rear){
visit(Q.data[i]);
i=(i+1)%MAXSIZE;
}
printf("\n");
return OK;
}
int main(){
Status j;
int i=0,l;
QElemType d;
SqQueue Q;
InitQueue(&Q);
//入队10个元素
for(int i =0;i< MAXSIZE-1; i++){
EnQueue(&Q,i);
}
QueueTraverse(Q);
printf("依次出队:");
for(l=1;l<=MAXSIZE;l++)
{
DeQueue(&Q,&d);
printf("d= %d,",d);
}
return 0;
}
- 链式队列
#include
#include
#include
typedef struct node{
int data;
node *next;
}node,*pNode;
typedef struct{
pNode front;
pNode rear;
}Queue,*pQueue;
void init(pQueue pq){
pq->front = pq->rear = (pNode)malloc(sizeof(node));
}
void push(pQueue pq,int x){
pNode pNew = (pNode)malloc(sizeof(node));
pNew->data = x;
pNew->next = NULL;
pq->rear->next = pNew;
pq->rear = pNew;
}
void pop(pQueue pq,int *e){
pNode pTemp = (pNode)malloc(sizeof(node));
pTemp = pq->front->next;
*e = pTemp->data;
pq->front->next = pTemp->next;
free(pTemp);
}
int main()
{
int i, e;
Queue q;
init(&q);
for(i=0;i<10;i++)
{
push(&q, i);
}
pop(&q, &e);
printf("%d\n", e);
pNode p = q.front->next;
while (p != NULL) {
printf("%d ", p->data);
p = p->next;
}
return 0;
}