LSGAN (Least Squares Generative Adversarial Networks)

Paper: https://arxiv.org/pdf/1611.04076.pdf
Ｇithub:
https://github.com/Hansry/PyTorch-GAN

1.前言

传统GAN出现的问题: 传统GAN, 将Discriminator当作分类器，最后一层使用Sigmoid函数，使用交叉熵函数作为代价函数，容易出现梯度消失和collapse mode等问题，具体原因参考本博客Wasserstein GAN。
LSGAN主要解决关键： 使用最小二乘损失代替交叉熵损失，解决了传统GAN生成的图片质量不高以及训练过程不稳定这俩个缺陷。

为什么使用最小二乘法能够改善传统GAN存在的问题？

1.避免梯度消失
文章指出，传统的GAN在使用生成的“fake”图片(已被Discriminator分类为正样本) 来更新Generator的参数的时候，会造成梯度消失，尽管该生成的"fake"图片数据离真实样本的数据还有一定的距离。当使用最小二乘来作为Discriminator的代价函数的时候，最小二乘会将生成的“fake”图片拉向决策边界，这里的决策边界穿过真实样本，可以使得LSGANs生成的图片更接近真实的数据。如文章中下图所示：

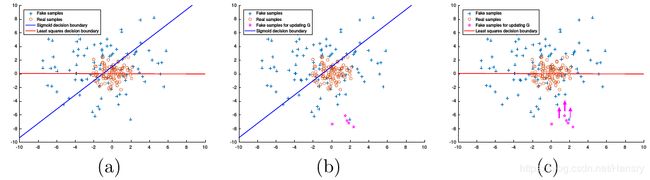
俩种不同损失函数的区别：(a)上图蓝色线代表交叉熵代价函数的Sigmoid决策边界，红色线代表最小二乘的决策边界。值得注意的是，对于成功的GANs学习过程，决策边界应该穿过真实样本分布，除非学习过程已经饱和了。(b)对于Sigmoid 交叉熵损失函数，当生成的“fake”图片被归类在决策边界正确的一边的时候(correct side)，得到的误差非差小以至于不能更新Generator，尽管这些数据离决策边界很远，也即离真实样本很远。©最小二乘损失函数会惩罚离决策边界很远的数据，使之朝着决策边界迈进，避免了梯度消失。

2.使训练过程更加稳定

由于GANs学习过程不稳定导致GANs训练困难。特别的，对于传统的由于其存在梯度消失的问题，所以很难更新Generator,造成训练困难。而LSGANs基于离边界的距离而对生成的样本进行惩罚，一定程度上避免了梯度消失，减缓了训练困难的问题。

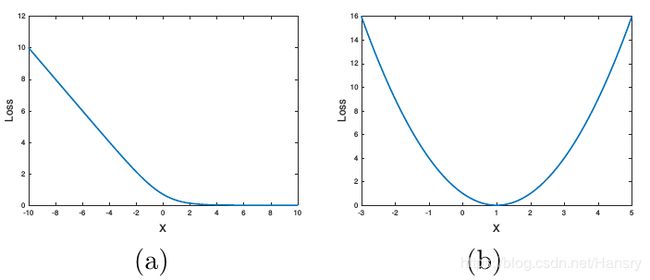
上图中，(a) 为Sigmoid交叉熵损失函数; (b)为最小二乘损失函数

文章的贡献：

• 提出最小二乘损失函数，在最小化LSGAN目标函数的时候也在最小化皮尔森${\chi }^2$散度(Pearson ${\chi }^2$ 散度)。
• 设计了俩种LSGANs, 其中一个用于图片生成(112x112分别率)，可生成高质量的图片。另一网络用于多类别任务，文章使用了中国字作为测试。

２. 传统的GAN

GAN的学习过程即同时训练Discriminator (D)和Generator (G)的过程，Ｇ从高斯分布的变量$z$, 学习潜在变量${\theta }_g$，来产生分布$p_g$，使得该分布与真实分布越接近越好。因此，Ｇ学习的是一个映射过程，通过$G\left(\mathbf{z};{\theta }_g\right)$变量映射空间来产生分布。另一方方面，Ｄ是一个分类器，来判断Ｇ产生的分布是否与真实样本接近，通过变量空间$D\left(\mathbf{x};{\theta }_d\right)$判断是否一样，同样的也是一个映射。传统GAN的代价函数如下：

${\min }_G{\max }_D{V}_{\mathrm{G}\mathrm{A}\mathrm{N}}(D,G)={\mathbb{E}}_{\mathbf{x}\sim p_{data}(\mathbf{x})}[\log D(\mathbf{x})]+{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}[\log (1-D(G(\mathbf{z})))]$　(公式1)

这里稍微解释下：

• 整个式子由两项构成。$x$表示真实图片，$z$表示输入$G$网络的噪声或者高斯分布数据，而$G(z)$表示$G$网络生成的图片。
• $D(x)$表示$D$网络判断真实图片是否真实的概率（因为$x$就是真实的，所以对于$D$来说，这个值越接近1越好）。而$D(G(z))$是$D$网络判断$G$生成的图片的是否真实的概率。
• $G$的目的：$D(G(z))$是$D$网络判断$G$生成的图片是否真实的概率，$G$应该希望自己生成的图片“越接近真实越好”。也就是说，$G$希望$D(G(z))$尽可能得大，这时$V(D,G)$会变小。因此我们看到式子的最前面的记号是$mi{n}_G$。
• $D$的目的：$D$的能力越强，$D(x)$应该越大，$D(G(x))$应该越小。这时$V(D,G)$会变大。因此式子对于$D$来说是求最大(max_D)

３. Least Squares Generative Adversarial Networks

LSGANs在Discriminator上使用a-b编码策略，简单来说就是用a来代表“fake”数据，用b来代表“real”数据。LSGANs的目标函数为：

${\min }_D{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(D)=\frac{1}{2}{\mathbb{E}}_{\mathbf{x}\sim p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}(\mathbf{x})}\left[(D(\mathbf{x})-b{)}^2\right]+\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z}))-a{)}^2\right]$

${\min }_G{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(G)=\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z}))-c{)}^2\right]$　　(公式2)

其中c代表生成器为了让判断器认为生成的数据是真实分布数据而定的值。在文章中作者设置$a=c=1,c=0$。

同时在文章中，作者列出了传统的GAN其实在优化的是JS散度，具体参考Wasserstein GAN，

$C(G)=KL\left(p_{data}\Vert \frac{p_{data}+p_g}{2}\right)+KL\left(p_g\Vert \frac{p_{data}+p_g}{2}\right)-\log (4)$　(公式3)

化为JS散度为 $2JS\left(P_{data}\Vert P_g\right)-2\log 2$

因此当俩个分布没有重叠或者重叠部分可忽略的时候，$JS\left(P_{data}\Vert P_g\right)=0$, 因此此时的梯度就变为0了。

因此，对于作者提出的LSGANs, 研究了LSGANs损失函数和f散度 (f-divergence)之间的联系：

${\min }_D{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(D)=\frac{1}{2}{\mathbb{E}}_{\mathbf{x}\sim p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}(\mathbf{x})}\left[(D(\mathbf{x})-b{)}^2\right]+\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z}))-a{)}^2\right]$

${\min }_G{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(G)=\frac{1}{2}{\mathbb{E}}_{\mathbf{x}\sim p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}(\mathbf{x})}\left[(D(\mathbf{x})-c{)}^2\right]+\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z}))-c{)}^2\right]$　公式(4)

其中在$V_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(G)$添加${\mathbb{E}}_{\mathbf{x}\sim p_{data}(\mathbf{x})}\left[(D(\mathbf{x})-c{)}^2\right]$并不会影响优化过程，因为添加的项没有包含关于Ｇ的内容。

对Ｄ求导数

$D^{\ast }(\mathbf{x})=\frac{b{p}_{data}(\mathbf{x})+a{p}_g(\mathbf{x})}{p_{data}(\mathbf{x})+p_g(\mathbf{x})}$

因此对于公式4，我们可以得到
$2C(G)={\mathbb{E}}_{\mathbf{x}\sim p_{\mathrm{d}}}\left[{\left(D^{\ast }(\mathbf{x})-c\right)}^2\right]+{\mathbb{E}}_{\mathbf{x}\sim p_g}\left[{\left(D^{\ast }(\mathbf{x})-c\right)}^2\right]$
$={\mathbb{E}}_{\mathbf{x}\sim p_{\mathrm{d}}}\left[{\left(\frac{b{p}_{\mathrm{d}}(\mathbf{x})+a{p}_g(\mathbf{x})}{p_{\mathrm{d}}(\mathbf{x})+p_g(\mathbf{x})}-c\right)}^2\right]+{\mathbb{E}}_{\mathbf{x}\sim p_g}\left[{\left(\frac{b{p}_{\mathrm{d}}(\mathbf{x})+a{p}_g(\mathbf{x})}{p_{\mathrm{d}}(\mathbf{x})+p_g(\mathbf{x})}-c\right)}^2\right]$
$={\int }_{\mathcal{X}}{p}_{\mathrm{d}}(\mathbf{x}){\left(\frac{(b-c)p_{\mathrm{d}}(\mathbf{x})+(a-c)p_g(\mathbf{x})}{p_{\mathrm{d}}(\mathbf{x})+p_g(\mathbf{x})}\right)}^2\mathrm{d}x+{\int }_{\mathcal{X}}{p}_g(\mathbf{x}){\left(\frac{(b-c)p_{\mathrm{d}}(\mathbf{x})+(a-c)p_g(\mathbf{x})}{p_{\mathrm{d}}(\mathbf{x})+p_g(\mathbf{x})}\right)}^2\mathrm{d}x$

$={\int }_{\mathcal{X}}\frac{{\left((b-c)p_{\mathrm{d}}(\mathbf{x})+(a-c)p_g(\mathbf{x})\right)}^2}{p_{\mathrm{d}}(\mathbf{x})+p_g(\mathbf{x})}\mathrm{d}x$

$={\int }_{\mathcal{X}}\frac{{\left((b-c)\left(p_{\mathrm{d}}(\mathbf{x})+p_g(\mathbf{x})\right)-(b-a)p_g(\mathbf{x})\right)}^2}{p_{\mathrm{d}}(\mathbf{x})+p_g(\mathbf{x})}\mathrm{d}x$　　（公式6）

这是在Ｄiscriminator达到最优的时候，Generator的损失函数，如果设$b-c=1$和$b-a=2$的话，有：

$\begin{array}{rl}2C(G)& ={\int }_{\mathcal{X}}\frac{{\left(2p_g(\mathbf{x})-\left(p_{\mathrm{d}}(\mathbf{x})+p_g(\mathbf{x})\right)\right)}^2}{p_{\mathrm{d}}(\mathbf{x})+p_g(\mathbf{x})}\mathrm{d}x\\ & ={\chi }_{\mathrm{P}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{n}}^2\left(p_{\mathrm{d}}+p_g\Vert 2p_g\right)\end{array}$

其中${\chi }_{\mathrm{P}earson}^2$为Pearson ${\chi }^2$ divergence（皮尔森散度），因此在最优化Ｄ的情况下将优化变为了Pearson ${\chi }^2$ divergence,避免了使用JS散度下造成的梯度为0，其中需要满足b-c=1 且b-a=2。

４. 搭建的网络

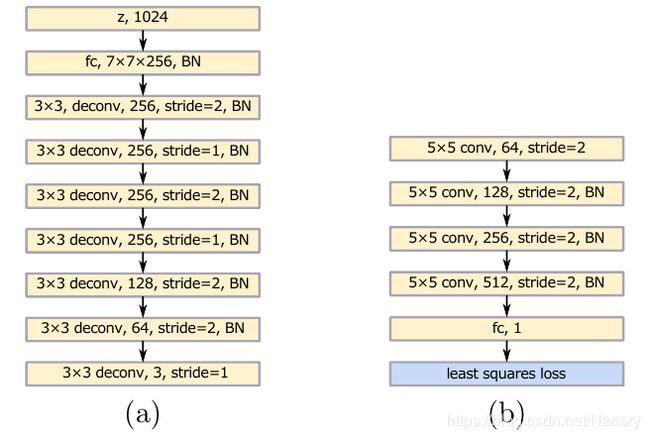
俩种参数的选择：
${\min }_D{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(D)=\frac{1}{2}{\mathbb{E}}_{\mathbf{x}\sim p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}(\mathbf{x})}\left[(D(\mathbf{x})-1{)}^2\right]+\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z}))+1{)}^2\right]$

${\min }_G{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(G)=\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z})){)}^2\right]$　(公式8)

和

${\min }_D{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(D)=\frac{1}{2}{\mathbb{E}}_{\mathbf{x}\sim p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}(\mathbf{x})}\left[(D(\mathbf{x})-1{)}^2\right]+\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z})){)}^2\right]$

${\min }_G{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(G)=\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z}))-1{)}^2\right]$　（公式9）

但是作者在文章又提了，这俩种参数在实践中的性能基本一样。

具体实验结果可看原文Least Squares Generative Adversarial Networks