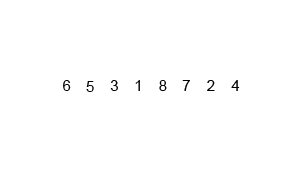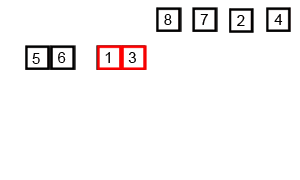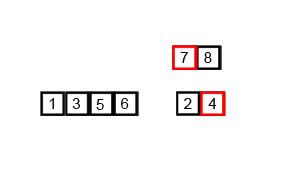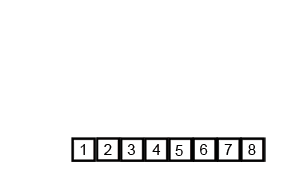AI笔试面试题库-Python题目解析
1、请用Python手写实现插入排序。
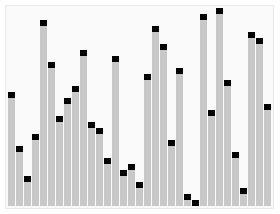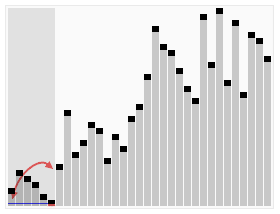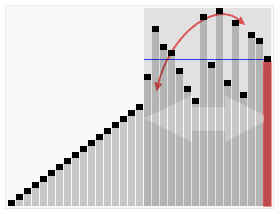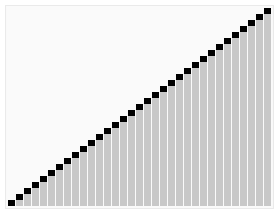
解析:插入排序(Insertion Sort)的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
算法执行步骤:
(1)从第一个元素开始,该元素可以认为已经被排序;
(2)取出下一个元素,在已经排序的元素序列中从后向前扫描;
(3)如果被扫描的元素(已排序)大于新元素,则将被扫描元素后移一位;
(4)重复步骤(3),直到找到已排序的元素小于或者等于新元素的位置;
(5)将新元素插入到该位置后;
(6)重复步骤(2)-(5)。
#Python实现
def insert_sort(ary):
n = len(ary)
for i in range(1,n):
if ary[i] < ary[i-1]:
temp = ary[i]
#待插入的下标
index = i
#从i-1 循环到 0 (包括0)
for j in range(i-1,-1,-1):
if ary[j] > temp :
ary[j+1] = ary[j]
#记录待插入下标
index = j
else :
break
ary[index] = temp
return ary2、请用Python手写实现快速排序。
解析:步骤:
(1)从数列中挑出一个元素,称为 “基准”(pivot);
(2)重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
(3)递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
换言之,快速排序时基于分治模式处理的,对一个典型子数组A[p...r]排序的分治过程为三个步骤:
(1)分解:A[p..r]被划分为俩个(可能空)的子数组A[p ..q-1]和A[q+1 ..r],使得A[p ..q-1] <= A[q] <= A[q+1 ..r];
(2)解决:通过递归调用快速排序,对子数组A[p ..q-1]和A[q+1 ..r]排序;
(3)合并。
QUICKSORT(A, p, r)
if p < r
then q ← PARTITION(A, p, r) //关键
QUICKSORT(A, p, q - 1)
QUICKSORT(A, q + 1, r)数组划分
快速排序算法的关键是PARTITION过程,它对A[p..r]进行就地重排:
PARTITION(A, p, r)
x ← A[r]
i ← p - 1
for j ← p to r - 1
do if A[j] ≤ x
then i ← i + 1
exchange A[i] <-> A[j]
exchange A[i + 1] <-> A[r]
return i + 1这是另外一个可视化图
Python实现代码如下:
#Python实现
def quick_sort(ary):
return qsort(ary,0,len(ary)-1)
def qsort(ary,left,right):
#快排函数,ary为待排序数组,left为待排序的左边界,right为右边界
if left >= right : return ary
key = ary[left] #取最左边的为基准数
lp = left #左指针
rp = right #右指针
while lp < rp :
while ary[rp] >= key and lp < rp :
rp -= 1
while ary[lp] <= key and lp < rp :
lp += 1
ary[lp],ary[rp] = ary[rp],ary[lp]
ary[left],ary[lp] = ary[lp],ary[left]
qsort(ary,left,lp-1)
qsort(ary,rp+1,right)
return ary3、请用Python手写实现堆排序。
解析:堆排序在 top K 问题中使用比较频繁。堆排序是采用二叉堆的数据结构来实现的,虽然实质上还是一维数组。二叉堆是一个近似完全二叉树 。
二叉堆具有以下性质:父节点的键值总是大于或等于(小于或等于)任何一个子节点的键值。每个节点的左右子树都是一个二叉堆(都是最大堆或最小堆)。
步骤:(1)构造最大堆(Build_Max_Heap):若数组下标范围为0~n,考虑到单独一个元素是大根堆,则从下标n/2开始的元素均为大根堆。于是只要从n/2-1开始,向前依次构造大根堆,这样就能保证,构造到某个节点时,它的左右子树都已经是大根堆。
(2)堆排序(HeapSort):由于堆是用数组模拟的。得到一个大根堆后,数组内部并不是有序的。因此需要将堆化数组有序化。思想是移除根节点,并做最大堆调整的递归运算。第一次将heap[0]与heap[n-1]交换,再对heap[0...n-2]做最大堆调整。第二次将heap[0]与heap[n-2]交换,再对heap[0...n-3]做最大堆调整。重复该操作直至heap[0]和heap[1]交换。由于每次都是将最大的数并入到后面的有序区间,故操作完后整个数组就是有序的了。
(3)最大堆调整(Max_Heapify):该方法是提供给上述两个过程调用的。目的是将堆的末端子节点作调整,使得子节点永远小于父节点。Python实现代码如下:
#Python实现
def heap_sort(ary) :
n = len(ary)
#最后一个非叶子节点
first = int(n/2-1)
#构造大根堆
for start in range(first,-1,-1) :
max_heapify(ary,start,n-1)
#堆排,将大根堆转换成有序数组
for end in range(n-1,0,-1):
ary[end],ary[0] = ary[0],ary[end]
max_heapify(ary,0,end-1)
return ary
最大堆调整:将堆的末端子节点作调整,使得子节点永远小于父节点
start为当前需要调整最大堆的位置,end为调整边界
def max_heapify(ary,start,end):
root = start
while True :
#调整节点的子节点
child = root*2 +1
if child > end : break
if child+1 <= end and ary[child] < ary[child+1] :
#取较大的子节点
child = child+1
#较大的子节点成为父节点
if ary[root] < ary[child] :
#交换
ary[root],ary[child] = ary[child],ary[root]
root = child
else :
break4、请用Python手写实现归并排序。
解析:归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组,再合并数组。先考虑合并两个有序数组,基本思路是比较两个数组的最前面的数,谁小就先取谁,取了后相应的指针就往后移一位。然后再比较,直至一个数组为空,最后把另一个数组的剩余部分复制过来即可。
再考虑递归分解,基本思路是将数组分解成left和right,如果这两个数组内部数据是有序的,那么就可以用上面合并数组的方法将这两个数组合并排序。如何让这两个数组内部是有序的?可以再二分,直至分解出的小组只含有一个元素时为止,此时认为该小组内部已有序。然后合并排序相邻二个小组即可。
Python实现代码如下:
#Python实现
def merge_sort(ary):
if len(ary) <= 1 : return ary
num = int(len(ary)/2) #二分分解
left = merge_sort(ary[:num])
right = merge_sort(ary[num:])
return merge(left,right) #合并数组
def merge(left,right):
'''合并操作,
将两个有序数组left[]和right[]合并成一个大的有序数组'''
#left与right数组的下标指针
l,r = 0,0
result = []
while l5、请创建一个函数检查一个词是否具有回文结构,使用 Python 进行编写。
解析:
def huiwen(str):
if len(str)==1:
return True
else:
return str[0]==str[-1] and
huiwen(str[1:-1])