Python数据科学numpy的运算、分布函数和矩阵

本文介绍numpy的常用运算、统计分布函数和矩阵的基础用法

numpy的一元多元运算，给我们做数据处理分析做基础，忘记的时候可以查看文档，常用的理解记忆就行。以下代码演示前提均以import numpy as np为前提

1. 一元运算：

• 运算函数：
  np.abs(x)/np.fabsx) -绝对值/浮点数绝对值;
  np.sqrt(x) -开平方根;
  np.square(x) -平方
  np.log(x)/np.log2(x)/np.log10(x) -取log对数值
  np.cell(x)/np.floor(x)/np.rint(x) -类似数学的进一法/退一法/四舍五入

• 统计函数：
  np.sum(a) -求和
  np.mean(a) -均值
  np.average(a,axis=0,weights=[10,5,1]) -加权平均，weight是权重属性
  np.std(a)/np.var(a) -标准差 /方差
  np.min(a)/np.max(a) -最小值/最大值
  np.ptp(a) -极差 np.median(a) -中位数
  np.argmin(a)/np.argmax(a) -返回将成一维后最小值最大值的索引值

• 三角函数：
  np.sin() np.cos() np.tan() 普通型三角函数
  np.sinh() np.cosh() np.tanh() 双面型三角函数

• np.exp() 指数值
  np.sign 符号值

下面演示一下运算函数的np.ceil()/np.floor()/np.rint()和统计函数的np.argmin()/np.argmax()

a1 = np.array([[90.2,70.6,88.1],[98.0,90.8,92.5],[-10.5,2.2,-98.7]])
result1 = np.ceil(a1)
result2 = np.floor(a1)
result3 = np.rint(a1)
print(result1)
print("========================")
print(result2)
print("========================")
print(result3)
print("========================")
print(a1)

结果分别显示进一法、退一法、四舍五入的效果。**值得注意的一点是，遇到负数是，数字会往大的方向。因为负数里面，数字越大值越小。**例如，np.floor(-1.2) 结果等于-2，代码例子也同理。
此外，最后一个打印是为了对比运算前后数组的变化，结论是运算后不改变原数组。

统计函数的np.argmax()/np.argmin()

a1 = np.array([[90.2,70.6,88.1],[98.0,90.8,92.5],[-10.5,2.2,-98.7]])
result1,result2,result3 = np.argmin(a1),np.argmax(a1),a1.flatten()
print(result1,result2)
print("这是数组一维的效果：",result3)

第一个打印结果，返回降成一维后的最大最小值的索引。为了方便我们检查最大最小值对应的索引位置，我也把数组降维打印出来，方便检查。
数组中最小值为-98.7，在第9个位置（最后一个），索引值8，正确。
数组中最大值为98.0，在第4个位置，索引值3，正确。

2. 二元运算

• np.maximum(x,y) np.fmax() 最大值 浮点数
  np.minimum(x,y) np.fmin() 最小值 浮点数
  np.mod(x,y) 模运算
  np.copysign(x,y) 将y中的各值的符号值赋值给x的对应元素

这里的运算函数用得比较少，不做过多的演示。

3. 三元运算

• np.where(判断或布尔值,True返回值,False返回值) 像Excel的if函数
  且条件判断：np.where(np.logical_and(val>1,val<5),1,0)
  或条件判断：np.where(np.logical_or(age>50,salary>100000),1,0)

b1 = np.array([[[15,16,4],[80,22,28]],[[1,2,3],[56,23,1]]])
print(np.where(np.logical_and(b1>15,b1<20),1,0))
print("==================")
print(np.where(np.logical_or(b1>30,b1<10),1,0))
print("==================")
print(np.where(np.logical_not(b1>=10),1,0))

4.分布函数

• 均匀分布与正态分布

c1 = np.random.rand(10)
c11 = np.random.uniform(10,100,(2,3))
print("均匀分布：\n",c1,"\n",c11)

c2 = np.random.randn(6)
c22 = np.random.normal(2,1.2,(4,2))
print("正态分布：\n",c2,"\n",c22)

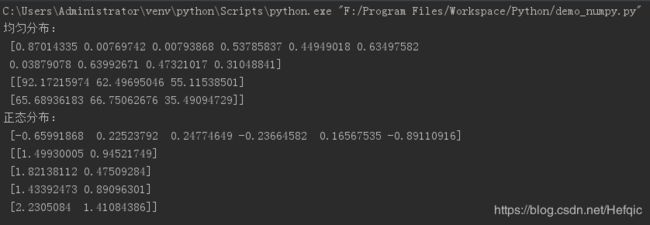
np.random.rand(x)：[0,1)的均匀分布，x为组成分布的个数
np.random.uniform(low,high,size)：[low,high)的均匀分布，size=shape数组形状

np.randn(x)：标准正态分布（均值0，方差1）x为组成分布的个数
np.normal(loc,scale,size)：正态分布，loc均值，scale方差，size=shape数组形状

• 随机分布和泊松分布

c3 = np.random.randint(1,100,(5,3))
c4 = np.random.poisson(0.7,(3,3))
print("随机整数分布：\n",c3)
print("泊松分布：\n",c4)

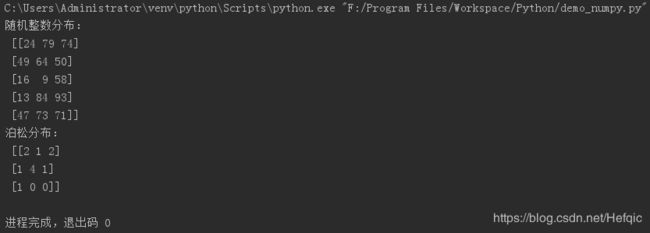
np.random.randint(low,high,size)：[low,high)的随机整数分布，size=shape
np.random.poisson(lam,size)：lam是事件发生概率，size=shape

5. 矩阵

矩阵乘法运算的两种情况

• 数组是由ndarray组成
• 数组是由matrix组成

用代码运行看看两者的差异

d1 = np.array([[2,4,2],[3,1,1]])
d2 = np.matrix([[6,1],[1,2],[8,3]])
d = np.matmul(d1,d2)
print(d1)
print("============")
print(d2)
print("============")
print(d)

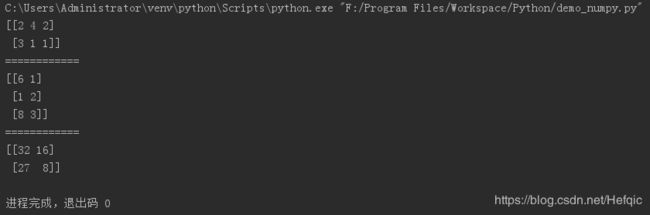
如果两个数据集是有包含用ndarray存的话（这里是一个ndarray，一个matrix），则需要用np.matmul()/np.dot()函数来进行乘法运算。

如果是用matrix存的话，则可以如下图代码所示，直接用运算符号，方便。

d3 = np.matrix([[1,2,3],[5,6,3]])
d4 = np.matrix([[2,6],[2,7],[5,1]])
d = d3*d4
print(d3)
print("============")
print(d4)
print("============")
print(d)

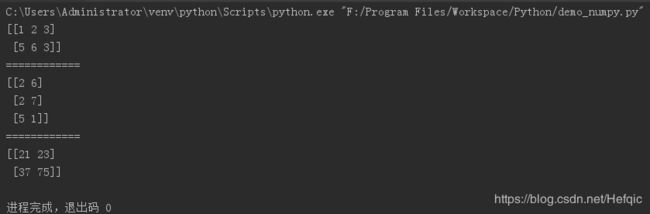
复习一下线性代数矩阵基本运算过程：
1 2 3 2 6
5 6 3 2 7
5 1

（2,2）乘（2,3）=（2*3）

符合（m,n）乘 （n,l）= （m*l）

=12+22+35 =21
=16+27+31 =23
=52+62+35 =37
=56+67+31 =75
（2*3）

还有一个广播机制，需要深入去研究一下才能理解透。
下次再见，坚持！