Datawhale《深度学习-NLP实践》Task5

1. 任务

1. 前馈神经网络、网络层数、输入层、隐藏层、输出层、隐藏单元、激活函数的概念。
2. 感知机相关；利用tensorflow等工具定义简单的几层网络（激活函数sigmoid），递归使用链式法则来实现反向传播。
3. 激活函数的种类以及各自的提出背景、优缺点。（和线性模型对比，线性模型的局限性，去线性化）
4. 深度学习中的正则化（参数范数惩罚：L1正则化、L2正则化；数据集增强；噪声添加；early stop；Dropout层）、正则化的介绍。
5. 深度模型中的优化：参数初始化策略；自适应学习率算法（梯度下降、AdaGrad、RMSProp、Adam；优化算法的选择）；batch norm层（提出背景、解决什么问题、层在训练和测试阶段的计算公式）；layer norm层。

2. 神经网络相关概念

2.1 前馈神经网络

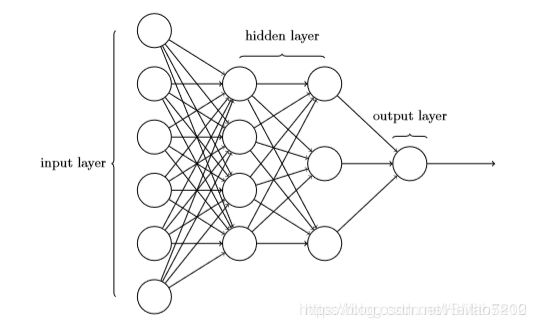
前馈神经网络也叫多层感知机(MLP),是典型的深度学习模型。前馈神经网络定义了一个映射$y=f(x;\theta )$,并且学习参数$\theta$的值，它能够得到最佳的函数近似。这个⽹络中最左边的称为输⼊层，其中的神经元称为输⼊神经元。最右边的，即输出层包含有输出神经元，在图片中，输出层只有⼀个神经元。中间层，既然这层中的神经元既不是输⼊也不是输出，则被称为隐藏层。上⾯的⽹络仅有⼀个隐藏层，但有些⽹络有多个隐藏层。对于构建复杂的系统，神经网络也会非常复杂，包含很多网络层，而且每一层的神经元个数也会不太一样。在神经⽹络中，以上⼀层的输出作为下⼀层的输⼊。这种⽹络被称为前馈神经⽹络。这意味着⽹络中是没有回路的——信息总是向前传播，从不反向回馈。

2.2 神经网络的结构

• 输入层（Input layer），众多神经元（Neuron）接受大量非线形输入消息。输入的消息称为输入向量。
• 输出层（Output layer），消息在神经元链接中传输、分析、权衡，形成输出结果。输出的消息称为输出向量。
• 隐藏层（Hidden layer），简称“隐层”，是输入层和输出层之间众多神经元和链接组成的各个层面。隐层可以有一层或多层。隐层的节点（神经元）数目不定，但数目越多神经网络的非线性越显著，从而神经网络的强健性（robustness）（控制系统在一定结构、大小等的参数摄动下，维持某些性能的特性）更显著。习惯上会选输入节点1.2至1.5倍的节点。
  这种网络一般称为感知器（对单隐藏层）或多层感知器（对多隐藏层），神经网络的类型已经演变出很多种，这种分层的结构也并不是对所有的神经网络都适用。
• 隐藏单元
• 激活函数

3. 感知机相关概念

3.1 add_layer

# 导入模块
import tensorflow as tf
import numpy as np

# 构造添加一个神经层的函数。
def add_layer(inputs, in_size, out_size, activation_function=None):
    Weights = tf.Variable(tf.random_normal([in_size, out_size]))
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
    Wx_plus_b = tf.matmul(inputs, Weights) + biases
    if activation_function is None:
        outputs = Wx_plus_b
    else:
        outputs = activation_function(Wx_plus_b)
    return outputs

3.2 导入数据

# 构建所需的数据
x_data = np.linspace(-1,1,300, dtype=np.float32)[:, np.newaxis]
noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32)
y_data = np.square(x_data) - 0.5 + noise
# 利用占位符定义我们所需的神经网络的输入。 tf.placeholder()就是代表占位符，这里的None代表无论输入有多少都可以，因为输入只有一个特征，所以这里是1

xs = tf.placeholder(tf.float32, [None, 1])
ys = tf.placeholder(tf.float32, [None, 1])

3.3 定义神经层

# 开始定义隐藏层,利用之前的add_layer()函数，这里使用 Tensorflow 自带的激励函数tf.nn.relu。
l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)
# 定义输出层。此时的输入就是隐藏层的输出——l1，输入有10层（隐藏层的输出层），输出有1层。
prediction = add_layer(l1, 10, 1, activation_function=None)
# 定义损失函数
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction),
                     reduction_indices=[1]))
# 使用优化器，让机器学习提升它的准确率。 
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)                    
# 使用变量时，都要对它进行初始化，这是必不可少的
init = tf.global_variables_initializer()
# 定义Session，并用 Session 来执行 init 初始化步骤。 （注意：在tensorflow中，只有session.run()才会执行我们定义的运算。）
sess = tf.Session()
sess.run(init)

3.4 模型训练

# 我们让机器学习1000次。机器学习的内容是train_step, 用 Session 来 run 每一次 training 的数据，逐步提升神经网络的预测准确性。 (注意：当运算要用到placeholder时，就需要feed_dict这个字典来指定输入。)

for i in range(1000):
    # training
    sess.run(train_step, feed_dict={xs: x_data, ys: y_data})
	# 每50步我们输出一下机器学习的误差。
   if i % 50 == 0:
        # to see the step improvement
        print(sess.run(loss, feed_dict={xs: x_data, ys: y_data}))	

3.5 可视化

# 构建图形，用散点图描述真实数据之间的关系。
# plot the real data
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.scatter(x_data, y_data)
plt.ion()#本次运行请注释，全局运行不要注释
plt.show()
# 显示预测数据。
# 每隔50次训练刷新一次图形，用红色、宽度为5的线来显示我们的预测数据和输入之间的关系，并暂停0.1s。

for i in range(1000):
    # training
    sess.run(train_step, feed_dict={xs: x_data, ys: y_data})
    if i % 50 == 0:
        # to visualize the result and improvement
        try:
            ax.lines.remove(lines[0])
        except Exception:
            pass
        prediction_value = sess.run(prediction, feed_dict={xs: x_data})
        # plot the prediction
        lines = ax.plot(x_data, prediction_value, 'r-', lw=5)
        plt.pause(0.1)
ax.plot(x_data, prediction_value, 'r-', lw=5)
plt.show()

4. 激活函数

激活函数（activation function）层又称 非线性映射 (non-linearity mapping) 层，作用是增加整个网络的非线性（即 表达能力 或 抽象能力）。深度学习之所以拥有 强大的表示能力 ，法门便在于 激活函数 的 非线性 。
如果不用激励函数（其实相当于激励函数是f(x) = x），在这种情况下你每一层节点的输入都是上层输出的线性函数，很容易验证，无论你神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机（Perceptron）了，那么网络的逼近能力就相当有限。正因为上面的原因，我们决定引入非线性函数作为激励函数，这样深层神经网络表达能力就更加强大（不再是输入的线性组合，而是几乎可以逼近任意函数）。

4.1 Sigmoid 函数

4.2 tanh 函数

4.3 Relu 函数

4.5 Leaky Relu 函数

4.6 参数化 Relu 函数

4.7 随机化 Relu 函数

4.8 ELU 函数

4.9 MaxOut(x) 函数

5. 深度模型的正则化.

5.1 参数范数惩罚.

在神经网络中，参数包括每一层仿射变换的权重和偏置，我们通常只对权重做惩罚而不对偏置做正则惩罚。 精确拟合偏置所需的数据通常比拟合权重少得多。 每个权重会指定两个变量如何相互作用。 我们需要在各种条件下观察这两个变量才能良好地拟合权重。 而每个偏置仅控制一个单变量。 这意味着，我们不对其进行正则化也不会导致太大的方差。 另外，正则化偏置参数可能会导致明显的欠拟合。

5.2 噪声注入

5.3 多任务学习

5.4 提前终止

5.5 稀疏表示

5.6 Dropout

参考资料

6. 深度模型中的优化

参考资料