NOIP2011提高组DAY2题解
链接:NOIP2011DAY1题解:https://blog.csdn.net/Hi_KER/article/details/82142423
T1:计算系数
考察知识:快速幂,组合数,数论
算法难度:XX+ 实现难度:XX+
分析:
那么:![]() 其中一项为:
其中一项为:![]()
所以我们求出![]() 就可以了
就可以了
求![]() :用公式
:用公式![]() 就可以了(当然,也可以用整数的唯一分解定理)
就可以了(当然,也可以用整数的唯一分解定理)
求![]() :用快速幂(两种写法:分治,二进制)
:用快速幂(两种写法:分治,二进制)
注意:防止中间变量溢出!!!
代码:
#include
const int MO=10007;
int a,b,k,n,m;
int C[1005][1005],ans;
int C_(int N,int M){
for(int i=0;i<=N;i++) C[i][i]=C[i][0]=1;
for(int i=2;i<=N;i++)
for(int j=1;j>=1;
}
return ret;
}
int main(){
scanf("%d%d%d%d%d",&a,&b,&k,&n,&m);
ans=C_(k,n);
ans=ans*q_pow(a,n)%MO;
ans=ans*q_pow(b,m)%MO;
printf("%d\n",ans);
return 0;
} T2:聪明的质监员
考察知识:前缀和,二分
算法难度:XXX 实现难度:XXX
分析:
我们分析后发现W与Y成反比,我们可以二分解决,先二分求满足Y<=S的最小W_x,然后比较当W=W_x和W_x-1时哪个更小就可以了
当然求和我们可以用前缀和思想实现,然而弱智的我开始居然用ST表,当然TLE
代码:
#include
#include
#include
#define ll long long
const int maxn=200005;
void scan(int& in_){//快速输入
char ch=getchar();
while(!(ch>='0'&&ch<='9')) ch=getchar();
in_=0;
while(ch>='0'&&ch<='9') in_=in_*10+ch-'0',ch=getchar();
}
int n,m,L[maxn],R[maxn],w[maxn],v[maxn],sum[maxn];
ll sum_v[maxn],S;
ll calc(int limt){
ll ret=0;
for(int i=1;i<=n;i++)
if(w[i]>=limt)
sum[i]=sum[i-1]+1,sum_v[i]=sum_v[i-1]+v[i];//前缀和思想
else
sum[i]=sum[i-1],sum_v[i]=sum_v[i-1];
for(int i=1;i<=m;i++){
ret+=(sum_v[R[i]]-sum_v[L[i]-1])*(sum[R[i]]-sum[L[i]-1]);
}
return ret;
}
int main(){
scanf("%d%d%lld",&n,&m,&S);
for(int i=1;i<=n;i++) scan(w[i]),scan(v[i]);
for(int i=1;i<=m;i++) scan(L[i]),scan(R[i]);
int L_=0,R_=1000000,ans;
while(L_<=R_){
int mid=(L_+R_)>>1;
if(calc(mid)<=S) R_=mid-1,ans=mid;//二分找答案
else L_=mid+1;
}
ll bigger=calc(ans-1)-S,smaller=S-calc(ans);//请自行理解
printf("%lld\n",bigger T3:观光公交
考察知识:贪心,模拟
算法难度:XXXX 实现难度:XXXX
分析:
我们先考虑k=0
定义T[i]表示公交车到达站台i时的时间,d[i]表示站台i-1->i之间的距离,late[i]表示站台i上所有人最晚到达的时间,E[i]表示人i的目的地编号,A[i]表示人i到达起点站的时间
那么我们可以得到:T[i]=max(T[i-1],late[i-1])+d[i]
再考虑k!=0
我们发现A[i]不变,所以要T[E[i]]尽量小
我们考虑在边d[i]处使用一次加速,那么我们需要求出这次加速所能减少的总时间
枚举所有边,求出减少最大时间,然后修改这条边(使用减少相当于边长度减少),更新T[]数组
重复k次我们就可以得到答案了
那么关键来了:我们怎么快速求减少总时间
我们定义数组:range[i]表示在将边d[i]长度减一后所能影响的最大站台编号
显然,当T[i]<=late[i],影响只能达到站台i
而T[i]>late[i]时影响可以达到range[i+1]
所以:range[i]=(T[i]>late[i])?range[i+1]:i;
求出所有range[i]后,我们维护前缀和num[i],num[i]表示目的地在站台1到站台i之间的总人数
那么,当d[i]减一时,减少总时间为:num[range[i]]-num[i-1]
细节在代码里
代码:
#include
#include
using namespace std;
int n,m,k,d[1005],A[10005],S[10005],E[10005];
int late[1005],num[1005],range[1005],T[1005],ans;
void cut_time(){
int max_=0,pos=0;
for(int i=n-2;i>1;i--)
range[i]=(T[i]>late[i])?range[i+1]:i;
for(int i=2;i<=n;i++) if(d[i]&&num[range[i]]-num[i-1]>max_)//d[i]>=0
max_=num[range[i]]-num[i-1],pos=i;
d[pos]--,T[pos]--,ans-=max_;
for(int i=pos;i<=n;i++)
T[i]=max(T[i-1],late[i-1])+d[i];
}
int main(){
scanf("%d%d%d",&n,&m,&k);
range[n]=range[n-1]=n;
for(int i=2;i<=n;i++) scanf("%d",d+i);
for(int i=1;i<=m;i++){
scanf("%d%d%d",A+i,S+i,E+i);
late[S[i]]=max(late[S[i]],A[i]);
num[E[i]]++;
}
for(int i=2;i<=n;i++)
num[i]+=num[i-1],T[i]=max(T[i-1],late[i-1])+d[i];
for(int i=1;i<=m;i++) ans+=T[E[i]]-A[i];
while(k--) cut_time();
printf("%d\n",ans);
return 0;
}
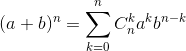
![\sum^{m}_{i=1}T[E[i]]-A[i]](http://img.e-com-net.com/image/info8/a91193414dc94ad3be9bee9519c29642.gif)