【数据分析与数据挖掘】三、单因子探索分析与可视化（中）

目录

3.数据分类

4.单属性分析

5.对HR.csv中的属性进行分析

---

3.数据分类

（1）定类（类别）：根据事物离散、无差别属性进行的分类，例如性别、名族；

（2）定序（顺序）：可以界定数据的大小，但不能测定差值。例如：收入：高、中、低；

（3）定距（间距）：可以界定数据大小的同时，可测定差值，但无绝对零点；（无零点，说明乘法、除法、比率是没有意义的）。例如：不能说20摄氏度是10摄氏度的两倍，这样的表述是不正确的；

（4）定比（比率）：可以界定数据大小，可测定差值，有绝对零点。例如：身高、体重、体积等；

4.单属性分析

异常值分析:离散异常值,连续异常值,常识异常值；

对比分析:绝对数与相对数,时间、空间、理论维度比较；

结构分析:各组成部分的分布与规律；

分布分析:数据分布频率的显式分析；

（1）异常值分析

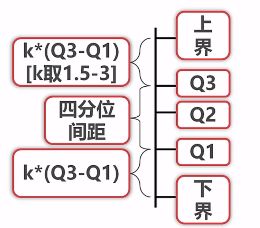
（a）连续异常值

上下界之间的是正常值，以外的就是异常值。根据K取得不同，异常值的测定也不一样，当k取1.5时，邻近边界的值算中等异常，当k取3时，就非常异常了。异常值的处理，我们可以直接舍弃，也可以直接去边界的值来代替异常值。

（b）离散异常值

离散异常值指的是：离散属性定义范围外的所有有值均为异常值。例如，空值是异常值、收入离散化以后，只有中高低三类，如果出现其他值，那就是异常值。这些异常值可以直接舍弃，也可以把所有的异常值当做一个单独的值来处理，也就是说，所有的异常值都是一个值，这个值用一个特殊的标记标记出来，和其他正常的值做一个区分。

（c）知识异常值

在限定知识与常识范围外的所有值均为异常值。如果身高，如果身高是10米，就不合符合常理。

（2）对比分析

我们是用数来进行分析的，根据数的类型可以分为两种两种比较方法：绝对数比较和相对数比较。

• 绝对数就是绝对的数字，比较数字、身高、评分等。

• 相对数是把几个有联系的指标进行联合构成一个新的数，这个数就是所谓的相对数。联合的方式有很对，那么相对数的种类就有很多。但是用得多的有以下几类：

  • 结构相对数：比如比率，产品合格率、考试通过率；

  • 比例相对数：总体内用不同的数值进行比较，比如传统意义上的三大产业，农业，重工业和服务业之类的比例，进行相互的比较，哪个产业相比于哪个产业发生了什么变化等。

  • 比较相对数：同一时空下的相似或者同一指标进行相比。例如：不同时期下同一商品的价格，不同电商互联网公司之间的待遇水平。

  • 动态相对数：一般是有时间概念在里面的，比如说物理上的速度、用户数量的增数等等。

  • 强度相对数：性质不同，但又相互联系的属性进行联合，比如说人均的概念，我国GDP占全球第二，但是人均GDP排在好几十，这个就是强度的概念。再比如粮食的亩产和密度的概念，都是强度相对数的比较范畴。

• 数据之间怎么比？

  • 时间上相比。例如：现在和过去比等；同比指的是，例如今年6月份和去年6月份的汽车销量，缓比：今年6月份和今年5月份比较。

  • 空间维度。不同国家，地区；一家公司的不同部门，不同公司间进行比较；

  • 经验与计 划。比如历史上失业率达到百分之几，就有可能发生暴乱。我们把自己国家的失业率和历史上发生的失业率比较，就是经验上的比较。计划上比较：我们做工作要排期，实时进度就要和计划进行比较。

（3）结构分析

结构分析其实可以看做是对比分析中的比例相对数的比较，它重点研究一个总体当中组成结构的方面的差异与相关性。结构分析可以分为静态结构分析和动态结构分析。

（a）静态结构分析

直接分析总体的组成，比如说分析农业、重工业、服务业的占比，分别是13% ，46%，41%，这样就确定了我国的产业结构，同时我们可以把这个产业结构和美国比，和其他国家比，来衡量我们的三大产业是否均衡，下一步应该怎么作决策。

（b）动态结构分析

以时间为轴，分析结构变化的趋势。比如十五期间三大产业的占比，与十一五期间的占比，来得知三大产业结构是如何变化的，就能反应国家性质上的变化方向。

（4）分布分析

（a）直接获得概率分布

（b）判断是不是正太分布

• 如果一个分布，偏态绝对值比较大，就不是正态分布；

• 如果正太分布的峰态系数定位3，那么峰态系数小于1或者大于5的，就肯定不是正太分布；

• 如果正太分布的峰态系数定位0，那么峰态系数小于-2或者大于2的，就肯定不是正太分布；

（c）极大似然

如果给出一连串的数，判断这些数和某个分布到底有多像，就可以用极大似然来表示。

5.对HR.csv中的属性进行分析

（1）对【“satisfaction_level”】分析

对于一个数据型的属性来说，none就是一个异常值。

import pandas as pd
import numpy as np

file = pd.read_csv("D:/HR1.csv")
sl = file["satisfaction_level"]
sl.isnull() # 用于判断是否有空值
print(sl[sl.isnull()] )# 判断异常值有几个
print( file[sl.isnull()] ) # 打印出为空的数据的具体情况
sl = sl.dropna() # 把为空的数据删除
# 查看均值、方差、偏态、峰态等，判断数据是否有异常
print(sl.mean())
print(sl.var())
print(sl.max())
print(sl.min())
print(sl.quantile(q=0.25)) # 上分位数
print(sl.quantile(q=0.75)) # 下分位数
# 查看数据分布
# 表示0-0.1之间的数有多少个数据；0.1-0.2之间的数有多少个.....
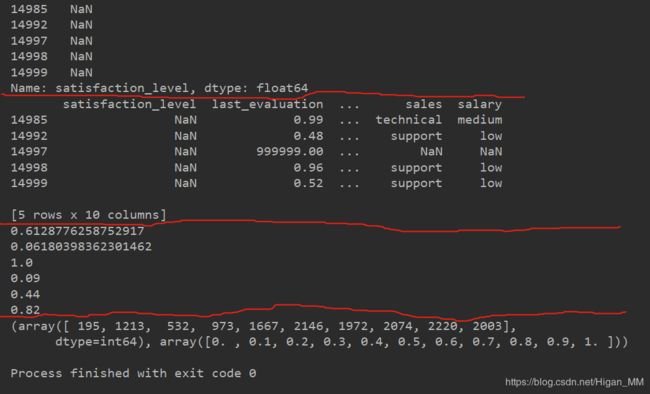
print(np.histogram(sl.values, bins=np.arange(0,1.1,0.1)))

结果如下：

(2)对【“last_evaluation”】分析

先求出均值，方差等值大概判断一下是否有异常数据，如果有，可以采用取四分位间距内的数，把数据异常舍去，代码如下：

import pandas as pd
import numpy as np

file = pd.read_csv("D:/HR1.csv")
le = file["last_evaluation"]
print(le.mean())  # 可以从结果中看出，该数据明显有异常数据
print(le.var())

# 取四分位间距内的数据
q_low = le.quantile(q=0.25)
q_hign = le.quantile(q=0.75)
q_interval = q_hign-q_low

k =1.5

# 取四分位数间距之间的值
le = le[leq_low-k*q_interval]

 # 重新求均值，方差
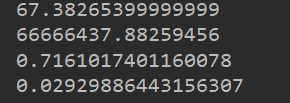
print(le.mean())
print(le.var())

结果为：

(3)对【“number_project”】分析

import pandas as pd
import numpy as np

file = pd.read_csv("D:/HR1.csv")
number_project = file["number_project"]
number_project.min()
number_project.max()

# 求每个数出现的次数
number = number_project.value_counts()
print(number)

# 获得每个数占总体的比例
pro = number_project.value_counts(normalize=True)
print(pro)

#排序
pro_new = number_project.value_counts(normalize=True).sort_index()
print(pro_new)

结果为：

(4)对【“average_montly_hours”】分析

注意：

 histogram 函数取得是左闭右开的数

 value_count（）取连续值的数量,取的是左开右闭的数

import pandas as pd
import numpy as np

file = pd.read_csv("D:/HR1.csv")
amh = file["average_montly_hours"]

# 取四分位间距内的数据
q_low = amh.quantile(q=0.25)
q_hign = amh.quantile(q=0.75)
q_interval = q_hign-q_low

k =1.5
amh = amh[amhq_low-k*q_interval]

# amh.max()+10 , 如果不加10，最大值很可能取不到
# histogram 函数取得是左闭右开的数
amh_new = np.histogram(amh.values, bins=np.arange(amh.min(), amh.max()+10, 10))
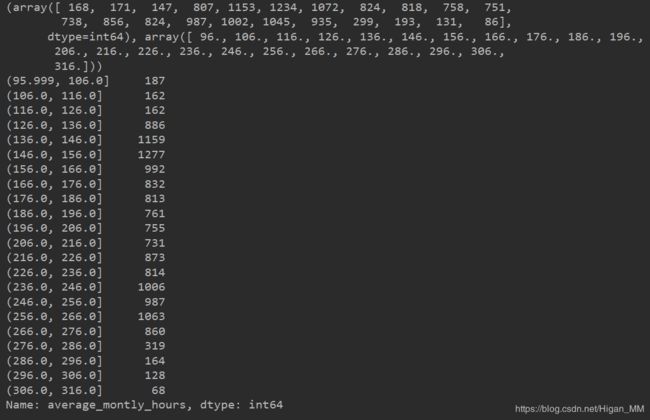
print(amh_new)

# 用value_count（）取连续值的数量,取的是左开右闭的数
amh = amh.value_counts(bins=np.arange(amh.min(), amh.max()+10, 10))
print(amh.sort_index())

结果为：

（5）简单对比分析操作

import pandas as pd
import numpy as np

# 删除表中的null值
file = pd.read_csv("D:/HR1.csv")
file =file.dropna(axis=0, how="any") # axis = 0表示删除null所在的行; how="any"表示这一行或列中有一个null值，就会删除；how="all"表示这一行或者列中全部是null值才会删除。

# 过滤掉["last_evaluation"]小于等于1和["salary"]为neme的数据
file = file[file["last_evaluation"]<=1][file["salary"]!="neme"]

# 对["salary"]进行分组,后求平均值
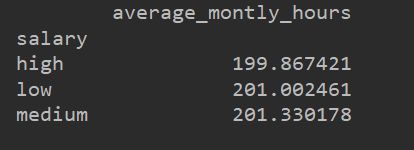
salary_group = file.groupby("salary").mean()
print(salary_group)

# loc[]进行切片, 即取某些属性
# :表示index, 全局的意思
loc = file.loc[:, ["last_evalution", "salary"]].groupby("salary").mean()
print(loc)

# 将salary进行分组high、low、medium，然后求average_montly_hours的极差，
# 可以分析high、low、medium三种层次下的average_montly_hours的情况
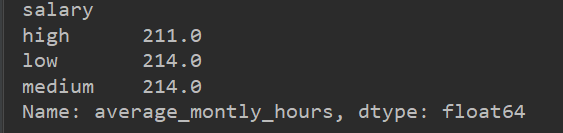
new = file.loc[:,["average_montly_hours","salary"]].groupby("salary")["average_montly_hours"].apply(lambda x:x.max()-x.min())
print(new)

结果为：

将salary分组后，对其他值求平均值，可以分析high、low、medium三个层次下的其他属性的情况。

将salary分组后，对其他值求平均值，可以分析high、low、medium三个层次下的【“average_montly_hours”】的情况。

用匿名函数的方法