数独Sudoku(DFS)
题目:
数独是一种填数字游戏,英文名叫 Sudoku。
玩家需要根据 9×9盘面上的已知数字,推理出所有剩余位置的数字,并满足每一行、每一列、每一个粗线九宫格内的数字包含有 1-9 的数字,且不重复。
输入描述:
多测试用例,输入T表示测试用例个数。
输入每一组数据,共 9 行 9 列,表示初始数独(其中 0 表示数独中的空位)。
输出描述:
输出共 9 行 9 列,表示数独的解。
Sample Input:
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
Sample Output:
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127
代码如下:
hang[ i ][ j ]表示第i行的数j是否已填,lie[ i ][ j ]表示第i列的数j是否已填,dyg[ i ][ j ]表示第i个3×3单元格的数j是否已填。
/*140ms*/
#includeE.数独挑战——2019年华南理工大学程序设计竞赛(春季赛):
链接:https://ac.nowcoder.com/acm/contest/625/E
单测试用例,题意与上述题目相同。
输入样例:
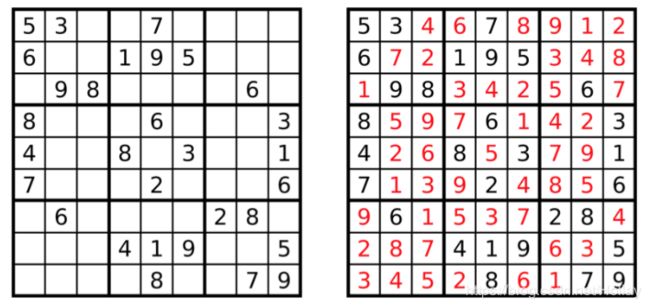
5 3 0 0 7 0 0 0 0
6 0 0 1 9 5 0 0 0
0 9 8 0 0 0 0 6 0
8 0 0 0 6 0 0 0 3
4 0 0 8 0 3 0 0 1
7 0 0 0 2 0 0 0 6
0 6 0 0 0 0 2 8 0
0 0 0 4 1 9 0 0 5
0 0 0 0 8 0 0 7 9
输出样例:
5 3 4 6 7 8 9 1 2
6 7 2 1 9 5 3 4 8
1 9 8 3 4 2 5 6 7
8 5 9 7 6 1 4 2 3
4 2 6 8 5 3 7 9 1
7 1 3 9 2 4 8 5 6
9 6 1 5 3 7 2 8 4
2 8 7 4 1 9 6 3 5
3 4 5 2 8 6 1 7 9
以下做法不用另开几个标记数组,但运行时间慢于上面那份代码,代码如下:
#include数独的舞蹈链(Dancing Links)做法:
(比dfs快很多,贴一下别人代码,待以后学习)
#include
#include
#include