【第四周】关于空间插值方法的学习-地质统计学相关概念

地质统计学:以区域化变量为基础，借助变差函数，研究既具有随机性又具有结构性，或空间相关性和依赖性的自然现象的一门科学。通过假设相邻的数据空间相关，并假定表达这种相关程度的关系可以用一个函数来进行分析和统计，从而对这些变量的空间关系进行研究。

2.地质统计学方法

    克里金插值法不仅考虑待估点位置与已知数据位置的相互关系，而且还考虑变量的空间相关性。而在进行克里金方法的学习之前，需要对地质统计学中的几个概念进行了解。

2.1 相关概念

2.1.1 随机变量、随机函数、随机场与区域化变量

    随机变量为一个实值变量，可根据概率分布取不同的值。每次取值（观测）结果$z$为一个确定的数值，称为随机变量$Z$的一个实现。随机函数是研究范围内的一组随机变量。当随机函数依赖于多个自变量时，称为随机场。
    例如，在三维空间中，设有单值函数$S=f(u,v,w)$，把$f$记做随机函数$Z$，其中$u,v,w$为随机变量，取决于多个随机变量的随机函数$Z$称为随机场。以空间内一点$x$($x$代表空间点位置，是一个三维或者二维坐标)作为随机变量的随机场可以被称之为一个区域化变量[1]。
    实际的矿井生产中的许多变量都可以被看作是区域化变量，例如毛煤煤质和工作面煤层厚度。对于毛煤煤质来说，可以看作是三维空间分布的点，点的值为毛煤的发热量、挥发分等煤质指标值；对于工作面煤层厚度来说，可以看作是二维空间分布的点，点的值为煤层厚度。
    区域化变量具有两个显著的特征，即随机性和结构性。首先，以毛煤煤质为例，煤炭的形成经过复杂生物化学过程与物理化学过程，毛煤煤质在空间某一点的煤质指标值是随机的，并且在后期的测量化验过程中，由于化验设备、人员操作等原因，也会产生随机误差。这就体现了区域化变量的随机性；其次区域化变量具有一般的或平均的结构性质，即变量在点$x$与偏离空间位移为$h$的点$x+h$处的数值$Z(x)$与$Z(x+h)$具有某种程度的自相关，这种自相关依赖于两点间的距离$h$及变量特征。而这种自相关性正是地质变量的连续性和关联性的一种体现，也就是其结构性的体现。

2.1.2变差函数

    变差函数(或叫变程方差函数，或变异函数)是地质统计学所特有的基本工具。它既能描述区域化变量的空间结构性变化，又能描述其随机性变化。
    假设空间点$x$只在一维的$x$轴上变化，则将区域化变量$Z(x)$在$x,x+h$两点处的值之差的方差之半定义为$Z(x)$在$x$轴方向上的变差函数记为$\gamma (x,h)$，既有:

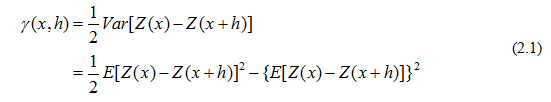
    公式(2.1)是变差函数的理论公式，在实际的应用场景中，只能得到已知点上的平均值，而此处需要知道的却是整个定义域上变量的平均值。只有在平稳条件下才能基于平均值进行预测，需要对区域化变量$Z(x)$提出一些合理的假设[2]。
（1）二阶平稳假设
    当区域化变量$Z(x)$满足下列两个条件时，称其为二阶平稳或弱平稳：
①在整个研究区域内有$Z(x)$的数学期望存在，且等于常数，即：

    随机函数在空间上的变化没有明显趋势，围绕$m$值上下波动。
②在整个研究区域内，$Z(x)$的协方差函数存在且平稳，即只依赖于滞后$h$，而与$x$无关：

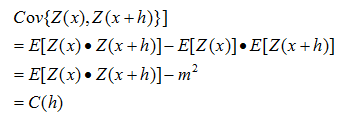
    在二阶平稳假设情况下，变差函数和协方差函数具有一下关系：

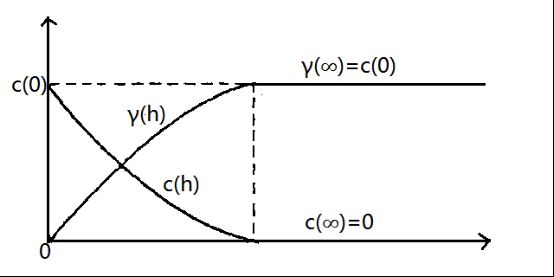
    既有：

    但在实际生产环境中，对于一些自然地质现象和随机函数，并不能满足二阶平稳假设，因此就提出了本征假设。
（2）本征假设
    当区域化变量$Z(x)$的增量$[Z(x)-Z(x+h)]$满足下列两个条件时，称其为满足本征假设或内蕴假设：

2.1.3结构分析

    通过区域化变量的空间观测值来构建相应的变差函数模型，以表征该变量的主要结构模型。
    通常我们通过已知点计算得到实验变差函数曲线，之后需要从理论变差函数模型中选择理论近似曲线，以此作为区域化变量的变差函数模型。为此，我们首先需要计算出实验变差函数。通过二阶平稳假设或者本征假设，可以知道区域化变量$Z(x)$的增量$[Z(x)-Z(x+h)]$不依赖于具体的位置$x$，只是依赖于滞后距$h$。对于不同的滞后距$h$，可以把区域化变量分隔成多个点对$Z(x_i),Z(x_i+h)(i=1,2,...,N(h))$（$N(h)$为被分隔的点对个数）。这样，就可以利用$[Z(x_i),Z(x_i+h){]}^2$求得不同滞后距$h$实验变差函数值${\gamma }^{\ast }(h)$：

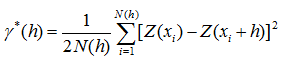
    如果把求得的${\gamma }^{\ast }(h)$作为纵轴，相应的滞后距$h$作为横轴，所作出的点值图成为实验变差函数云图，对实验变差函数云图进行拟合即可得到实验变差函数曲线图，如下图所示：

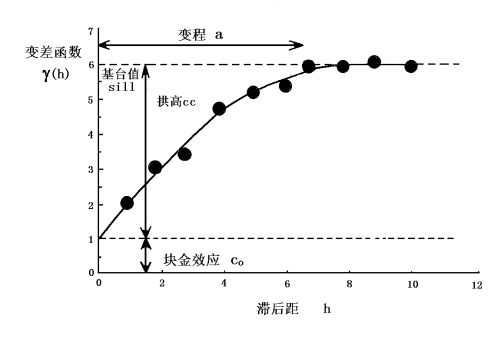
    实验变差函数曲线图可以体现出实验数据的空间相关性，空间上相近的采样点之间的相关性强，而相距较远的采样点之间的相关性较小，当超过一个最小相关性时，距离的影响就不大了[3]。 在变差函数模型中有如下四个重要的参数：
    变程(Range)：指区域化变量在空间上具有相关性的范围。在变程范围之内，数据具有相关性；而在变程之外，数据之间互不相关，即在变程以外的观测值不对估计结果产生影响。
    块金值(Nugget) ：变差函数如果在原点间断，在地质统计学中称为“块金效应”，表现为在很短的距离内有较大的空间变异性，无论$h$多小，两个随机变量都不相关。它可以由测量误差引起，也可以来自矿化现象的微观变异性。所以，在一定程度上块金值体现了误差的大小，块金值越小越精确。
    基台值(Sill)：代表变量在空间上的总变异性大小。即为变差函数在$h$大于变程时的值，为块金值$c_0$和拱高$c_c$之和，此时可认为空间相关性不存在。
    拱高为在取得有效数据的尺度上，可观测得到的变异性幅度大小。当块金值等于0时，基台值即为拱高。
    在得到实验变差函数曲线之后，通过该曲线选择合适的理论变差函数模型。之所以要选择理论变差函数模型的原因主要是所求取的变差函数云图中的平均值的数据点并不是互相独立，而是互相关联的。而且，由实验变差函数曲线计算的任一近似函数，可能会在变差函数云图中产生负的纵坐标点（差的平方）。而在常见的几种理论变差函数模型中不存在这样的矛盾[4]。
    设$Z(x)$为满足本征假设的区域化变量，则常见的理论变差函数有以下几类（$c$为基台值；$a$为变程；$h$为滞后距）：

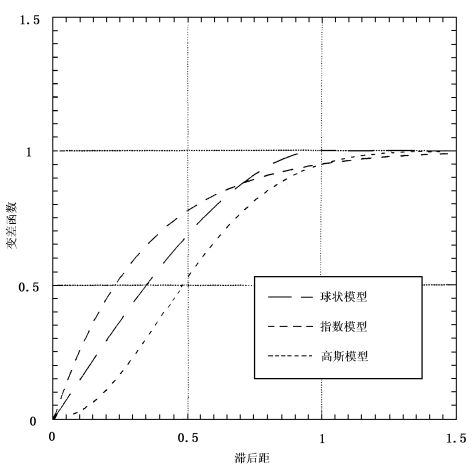
    球状模型、指数模型与高斯模型的变差函数图如下图所示：

2.1.4 变差函数参数的最优性检验

    变差函数是否符合实际，应该进行检验。一种实用的检验方法为“交叉验证法”（Cross-validation），检验标准是在各实测点，根据周围点计算的克里金估计值与该实测值的误差平方平均最小。
    估计误差的平方与克里金估计方差之比越接近1，则说明变差函数与实际的符合程度越高。

参考文献

[1]李晓军,王长虹,朱合华.Kriging插值方法在地层模型生成中的应用[J].岩土力学,2009,30(01):157-162.
[2]E.B.科瓦列夫斯基. 基于地质统计学的地质建模[M]. 北京:石油工业出版社, 2014. 19-21
[3]变差函数
[4]Chilès J P, Delfiner P. Geostatistics: Modeling Spatial Uncertainty[J]. 1999, 95(449 ).