O(1)复杂度的字符串查找算法设计

     Tips：这是为本人所在公司设计的查找子串的算法的文档。“发明”出来之后才发现杯具了……原来这货叫字典树，是早已经有的东西。计算熵倒是自己引入的，但是后面发现很多情况下得不偿失，实际实现中去掉了这个功能。以下为文档最初始的版本，并不跟手上已经实现的玩意完全符合。仅仅希望大家看了之后能有所启发，以下是正文。

   

1 简介

2 测试数据

3 算法原理介绍

  1.1 在数组查找单个字符

  1.2 在树查找字符串

  1.3 计算熵增益 构建决策树查找字符串

4 模糊查找

5 缺陷和优化

 

 

1 简介

本算法的应用场景为，在N个NWord长的字符串集合中，查找一个NWord长的字符串所在位置。 

根据理论预期和实际检验，目前为止基本实现了O（1）时间复杂度的查找。也就是说，无论N为多少，查找时间基本为常数。严格来说，查找时间跟N无关，仅跟字符串长度NWord有关。但是字符串长度大部分情况下不会超过一定范围（比如10-20个汉字），所以可认为：查找时间 = f(  NWord )  = f( 群名长度 ) = 常数。

本算法在设计中参考了两种算法：

1）根据ID3算法计算熵增益构建决策树。

2）参考暴雪游戏公司的哈希查找算法，使用字符串本身的值的一部分作为下标。

2 测试数据

算法Demo使用随机生成的大量字符串作为测试样本。主要变动参数有2个：N，查找的字符串样本集合的数量；NWord，待查找的字符串字节数，同时也是字符串样本集合每个元素的字节数。测试耗时单位为毫秒。查找内容为在有N个目标字符串的集合中进行查找N次查找，带查找字符串也从集合中抽取（即保证待查找字符串一定在字符串集合中）。

比较效率的目标算法为STL的unordered_map和暴雪的同样为O(1)复杂度的hash查找。机器环境为64位windows 7， Intel Core I5 四核CPU。

查询次数	目标字符串集合大小 即N	待查找字符串长度即NWord	stl::unordered_map	blizzard字符串查找算法	原创查找算法—精确模式	原创查找算法—模糊模式
1*10000	1*10000	20	64	9	11	3
2*10000	2*10000	20	137	18	31	5
3*10000	3*10000	20	238	26	48	12
4*10000	4*10000	20	301	34	42	22
5*10000	5*10000	20	340	42	77	21
6*10000	6*10000	20	468	49	88	18
7*10000	7*10000	20	489	58	110	33
8*10000	8*10000	20	556	66	92	34
9*10000	9*10000	20	636	75	117	39
10*10000	10*10000	20	662	85	117	38
1*10000	1*10000	40	60	10	10	3
2*10000	2*10000	40	120	17	20	6
3*10000	3*10000	40	200	25	32	10
4*10000	4*10000	40	290	33	41	13
5*10000	5*10000	40	315	41	58	17
6*10000	6*10000	40	390	49	68	22
7*10000	7*10000	40	432	57	74	27
8*10000	8*10000	40	495	69	87	30
9*10000	9*10000	40	568	75	101	34
10*10000	10*10000	40	636	84	108	39

结论：

当数据量N在1万到10万之间时，无论字符串长度为多少，以下成立：

使用STL内置的unordered_map算法时，每万次查找消耗时间在50~60毫秒左右

使用暴雪blizzard字符串查找算法时，每万次查询时间都稳定在8毫秒左右；

使用自定义算法精确查找时，每万次查询时间都稳定在10毫秒左右；

使用自定义算法模糊查找时，每万次查询时间都稳定在3-4毫秒左右。

3 算法原理介绍

  3.1 在数组查找单个字符

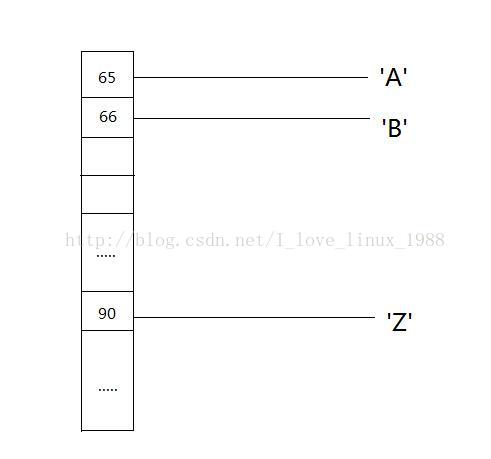
  我们先考虑在一个1维数组中查找NWord为1的字符串，也就是单个字节。如果我们直接把字节的值作为下标，那么O（1）的时间复杂度是很明显的。

3.2 在树查找字符串

考虑多个字节的字符串，就不能再使用1维数组来存储。可以把字符串切割为字节放在树结构之中。每个字节在本层子节点通过该字节的值来进行索引。这样，当需要进行查找时，即不使用深度遍历，也不需要使用广度遍历，只要遍历字符串的每一个字节，不断取字节值作为下标即可。

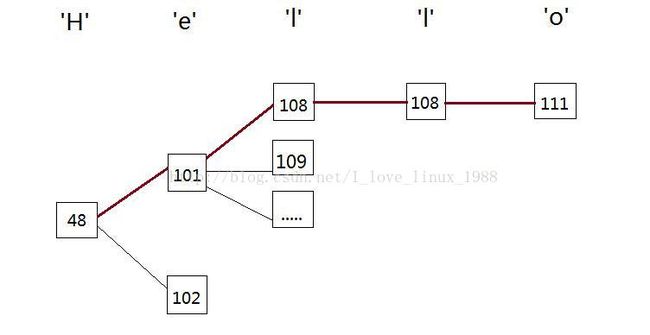
3.3 计算熵增益 构建决策树查找字符串

3.2中是顺序使用每一个字节的值作为下标。但是每个字符的重要性，或者说代表性，可以使不同的。假设我们在三个样本组成的集合中进行查找，即Hell，Heat，High。如果我们把3个词组织成树，可以根据根节点的选取组织不同的树。

我们考虑三个单词的字节1和字节3。如果我们在决策树中第一步判断的是单词的第3字节（也就是说以第3字节的值构建根节点的下级），那么可以一步到位查找出来，可以不进行后续的判断。如果第一步判断的是第1字节，那么就是在做无用功，还要进行后续判断。

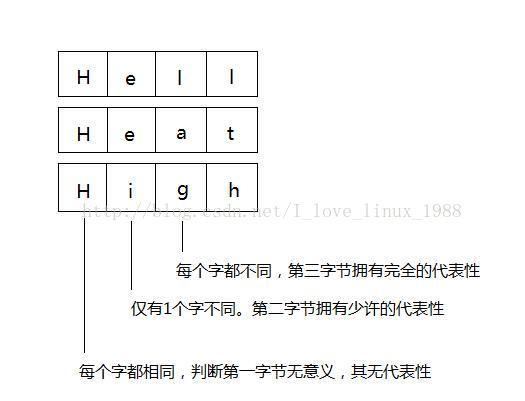
有NWord个字节，就要计算NWord次熵增益。每次计算熵增益的参数为所有字符串中相同位置的字节，即N个字符。 

我们令S为样本集合，A为某个字节，则字节A的熵增益的计算公式如下：

 

其中，是样本内所有N个字符串的总熵，这里取；是S的不同子集，这里就是某个字节取不同值的集合。是不同取值的数量；是总样本数量N。即是。例如第3字节的i，a，g分别是一个集合，其分别是1,1,1。第2字节的e，i分别是一个集合，其分别是2和1。我们根据公式计算二者的熵增益如下：

总熵 = log(2,N) = log(2,3) = 1.584

第三字节的熵增益 = log(2,3) - ( log(2,1)/3 + log(2,1)/3 + log(2,1)/3 ) =log(2,3) = 1.584  

第二字节的熵增益 = log(2,3) - ( log(2,2)/3 + log(2,1)/3) = log(2,3) - 1/3 = 1.251

也就是说，第三字节的“价值”更大，应该取第三字节在更靠近根节点的层次上。进一步地说，第三字节的熵增益等于总熵，也就是说其拥有完全的信息——只要判断第三字节就可以完成查找。

4 模糊查找与精确查找

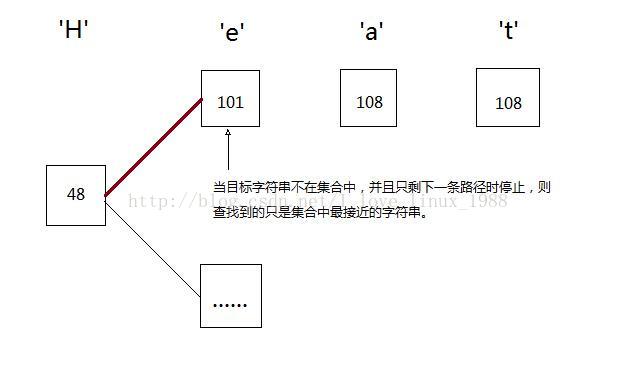
决策树查找之所以快，在于可以在适当的时机停止下来。参考下面的例子：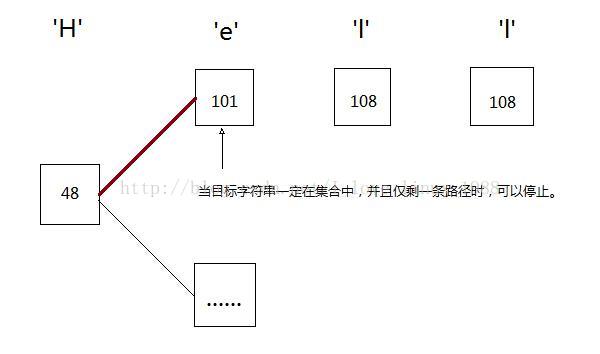

就如同第3节所说的，如果我们在树的某i层，对应所有字符串的第j个字节，如果每个字符串的j字节都两两不同，那么查找到该层的适当位置时并且子树数量仅为1时即可停止，因为接下来的必是要查找的字符串。比如例3的第3个字节——l，a，g——两两不同，我们只要判断第三字节即可。

但是如果集合中没有我们要查找的字符串，而查找算法执行到只剩下1个子树时，若此时停止，找到的就不是跟待查找字符串完全匹配的字符串，而仅仅是集合中最接近的。

5  缺陷和优化

     在最新的实现中，首先我去掉了计算熵增益的部分；否则插入时耗时太长。其次，为了应付当保存的字符串长度为60，数量大于等于10万条时内存的爆炸性增长，我把树节点的数据部分设置成动态分配。内存池使用了谷歌的je_malloc，否则大量的内存碎片会使内存回收变成大问题。