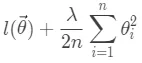预测概率的逻辑回归算法
原创: wk Refinitiv创新实验室ARGO 10月1日
"本篇文章包含部分数学公式,阅读时间约10分钟"
曾有报道说,性感女神安吉丽娜朱莉因确认携带致癌基因,患乳腺癌概率为87%,所以她选择主动切除乳腺。当时这篇报道给我的震惊在于女神的果断,因为我们常人怀有侥幸心理,不到万不得已绝舍不得给自己来一刀。 不过,如今我们学习机器学习,那视角就得小小切换一下:女神这 87%的患病概率是怎么计算得来的?如果以机器学习方法来预测,该选用什么样的算法? 说到概率预测,必然免不了提及今天要介绍的逻辑回归算法。而事实上,逻辑回归算法在医疗健康领域使用的确十分广泛。
以一个预测心脏病的例子来开始,假设我们收集了以下数据(事实上,我们应该搜集的正反例以及数据维度要比下图所示的多很多。且这个例子也以心理学中A型人格的发现闻名)
通过这些数据,建立一个逻辑回归算法预测模型。模型在通过学习完以上数据后,就能对某个未知心脏病的人员进行概率预测。比如,老张的各项指数如下
模型在输入老张的各项参数以后,将预测出: 老张同志,心脏病可能性75%。是不是听上去还有点靠谱? 那我们就来看看这个算法是什么原理,如何训练并使用python实战吧。
一 初识逻辑回归
逻辑回归是一种比较简单的算法。一般认为, 逻辑回归模型=线性回归+Sigmoid函数。 所以,我们先从线性回归和Sigmoid函数说起,当两者组合,就得到了逻辑回归的预测函数。
a 线性回归
先看最简单的单变量线性回归预测函数,对于任意输入的变量X, 假定Y输出符合公式如下:
这就是我们所熟知的针对单个变量的线性回归模型的预测函数。如果将单变量模型扩展到多变量模型, 就得到多变量的线性模型预测函数:
通过训练样本训练出其中的参数![]() 和b,将得到一个线性回归模型。但线性回归缺点比较明显,比如,不适宜用于二分类问题。
和b,将得到一个线性回归模型。但线性回归缺点比较明显,比如,不适宜用于二分类问题。
那怎么样让线性回归应用于二分类问题呢? 由此,Sigmoid函数隆重登场。
b Sigmoid函数
Sigmoid函数在机器学习中应用广泛,除了逻辑回归(在逻辑回归里,它叫logistic函数)以外,它还用作神经网络的激发函数。它的数学表示如下
Sigmoid函数之所以叫做Sigmoid函数,是因为它的形状函数图形如下图所示,是一个苗条的'S'型。它最初被用来描述人口的增长。
它有三个典型特点:定义域![]() ;值域(0,1),符合概率的范围 ; 函数连续且满足
;值域(0,1),符合概率的范围 ; 函数连续且满足![]() ,便于运算。此外,比较重要的一点是,它的函数图形跟阶跃函数相似,但又比阶跃函数光滑。
,便于运算。此外,比较重要的一点是,它的函数图形跟阶跃函数相似,但又比阶跃函数光滑。
c 组装逻辑回归预测函数
就机器学习的常规套路而言,一个机器学习的算法核心是定义预测函数。 通过前面介绍的线性模型和Sigmoid函数,就可以组装得到逻辑回归的预测函数。 假定样本标签为0或1,逻辑回归将预测某个样本为1(或者0)的概率, 其预测函数如下:
由于这个函数相对简单,复杂度低,在特征数据维度极大、数据量极多的情形下,其他许多机器学习模型在工程效率上已经无能为力时,这个算法还能发挥巨大的作用。所以,逻辑回归在CTR(广告点击预估)以及打车价格测算上有非常大的优势,应用也比较多。
通过以上的介绍,相信读者对逻辑回归的模型有了一个初步的认识。 但是,周志华教授的西瓜书将逻辑回归称之为“对数几率回归模型”,李航讲逻辑回归时,又引入了“最大熵的学习模型”。这又是怎么回事?为了更详细的了解逻辑回归模型,我们将对逻辑回归进行认知升级并介绍它的代价(损失)函数。
二 逻辑回归认知升级
一般认为逻辑回归是广义线性模型,其决策边界(或者对于数据区域的划分边界,NG的图帮我们理解决策边界这一概念)是线性函数。
逻辑回归是“对数几率回归模型”,是广义线性模型。虽名为回归,但实质上是分类,而凡是分类预测概率模型,又遵循的是“最大熵原理”。
i) 广义线性模型
前面提到,线性模型不能很好的解决二分类问题,实际上不光是二分类问题,很多现实情况都要求输入空间到输出空间是非线性映射。这个时候,就需要在线性回归模型的预测值和真实的标记间建立一个联系函数(link function) g(.) 。对线性模型的输出加上这个联系函数,就可以得到了一个广义线性模型,数学表达式如下:
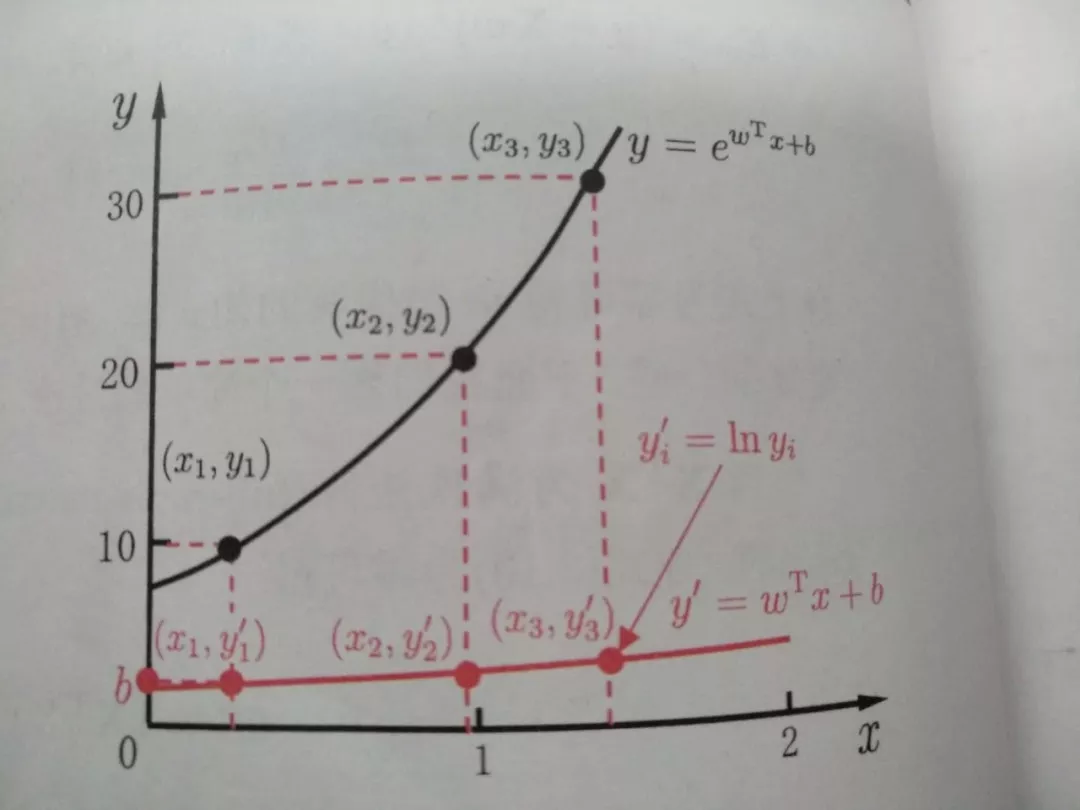
例如,使用“对数线性回归”,联系函数取ln(.),能看到其线性预测值与真实标记关系如下图所示,实现了从输入输出的非线性转换。
图片来源:周志华的《机器学习》
因此,读者朋友们也能想到,逻辑回归也属于广义线性模型。 但是其联系函数是什么,其线性回归的输出预测的又是什么?
ii) 对数几率回归模型
对于二分类任务,其输出值只有0 或者 1,我们更希望找到一个函数(g(.)的逆),将线性模型的输入空间到输出空间的转换变得能像阶跃函数一样,在线性模型输出小于0时为0,大于0时为1。是的,Sigmoid函数就十分符合这一特征,将其带入线性模型中,就得到了我们之前介绍的逻辑回归预测函数。通过将该预测函数适当的变换,得到如下公式:
对等式左边稍做解释:y为预测值为正样本的概率 ,1-y为结果为负样本的概率。预测正的概率和预测负的概率的相对比值y/(1-y),我们称之为“几率”(odds),几率取对数称之为“对数几率”,这就是逻辑回归被称为对数几率回归的由来。 由此可知,对数几率函数也就是该广义线性模型的联系函数。
值得一提的是,“对数几率”函数有很多良好的数学性质,尤其它是任意阶可导的凸函数,在最优化算法里可以直接用于求解最优解。
接下来的问题便是它的代价(损失)函数和对应的参数估计求解了。我们使用最大似然估计方法作为其代价函数,其背后又离不开最大熵原理的支撑。对于一个二分类到多分类的扩展,我们也稍稍提及。
三 代价函数、参数估计和多分类问题
在对逻辑回归进行训练时,一般采用“最大似然估计”对模型进行参数估计。也就是,我们认为每个样本属于真实标签的概率越大越好。假定二分类有:
那么,代价函数为对数似然函数:
参数估计于是化为对该函数求极大值问题。 因为这个函数求极值在数学上可被证明是一个凸优化问题,所以通过梯度下降或者是牛顿法一定可以取得最优解。这部分我们不详细展开,以后会有专门的数学篇,来集中阐述凸优化问题和极值问题的求解方法。
那问题来了,为什么在使用线性回归时,用最小二乘做代价函数,而在概率预测模型中,我们使用最大似然方法来做参数估计呢?除去最大似然估计的数学极值求解更容易以外,机器学习大师李航在《统计学习方法》中也提到了最大熵原理。
最大熵原理
李航说,"最大熵原理是概率模型学习的一个准则。最大熵原理认为,学习概率模型时,在所有可能的概率分布中,熵最大的模型是最好的模型” 。通俗的讲,假定一个模型预测结果是某概率函数,那么,对其样本按该概率函数求条件熵,条件熵最大的概率函数才是最好的函数。而李航在他的书中证明了熵公式的极大化模型等价于模型的最大似然估计。
代价函数的正则化项
逻辑回归也会面临过拟合的问题,所以在训练时,代价函数一般会加上正则项。强调正则化项的另一目的在于在本文之后介绍的sklearn参数部分,会介绍到正则项的选择参数。对于逻辑回归的正则项,一般选择L1正则项或者是L2正则项。其中,L1正则项使用绝对值,是一个不连续的函数:
L2正则项连续且加上正则项不仅连续,而且该函数求极值依然满足凸优化条件:
此外,在介绍sklearn参数时,还会涉及到如何将一个二分类问题转化为多分类问题,一般常见的方法的思想都是生成多个二分类器,由多个二分类器对数据进行判断。这些方法我们不展开。同时,对应逻辑回归的多分类模型还有一种另外一种机器学习算法叫Softmax算法,逻辑回归模型算是该算法二分类的特例。有兴趣的读者可以自己了解一下,本公众号也会在之后推出多分类的专题文章。
四 sklearn库逻辑回归参数介绍
在sklearn库中存在有LogisticRegressionCV, LogisticRegression两种不同的构造函数。其中,LogisticRegressionCV对数据级进行交叉验证来设定超参数C(也就是前文所说的正则化系数λ的倒数)。而LogisticRegression需要提前设置该参数。我们主要来看LogisticRegression构造函数。
构造函数参数如下:
logreg=linear_model.LogisticRegression(penalty='l2',
dual=False, tol=0.0001, C=1.0, fit_intercept=True,
intercept_scaling=1, class_weight=None,
random_state=None, solver='sag', max_iter=100,
multi_class='ovr', verbose=0, warm_start=False, n_jobs=1)
参数各项意义为:
[penalty] 正则项, L1还是L2。 如果L2还是会出现过拟合,可以使用L1,L1算法可以导致特征的稀疏化。
[tol] 停止求解的标准,float类型,默认为1e-4。就是求解到多少的时候,停止,认为已经求出最优解。
[c] 正则化系数λ的倒数,float类型,默认为1.0。必须是正浮点型数。像SVM一样,越小的数值表示越强的正则化。
[fit_intercept] 是否存在截距或偏差,bool类型,默认为True。
[intercept_scaling] 仅在正则化项为”liblinear”,且fit_intercept设置为True时有用。float类型,默认为1。
[class_weight] 用于标示分类模型中各种类型的权重,可以是一个字典或者’balanced’字符串,默认为不输入,也就是不考虑权重,即为None。如果选择输入的话,可以选择balanced让类库自己计算类型权重,或者自己输入各个类型的权重。某种类型样本量越多,则权重越低,样本量越少,则权重越高。权重设定在样本误分类影响严重或者是样本高度失衡条件下需要仔细权衡该值的设置。
[random_state] 随机数种子,int类型,可选参数,默认为无,仅在正则化优化算法为sag,liblinear时有用
[solver] 开源实现的一些优化算法。即newton-cg, lbfgs, liblinear, sag, saga。默认为liblinear。solver参数决定了我们对逻辑回归损失函数的优化方法,有四种算法可以选择,分别是:
-
liblinear:使用了开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数。
-
lbfgs:拟牛顿法。
-
newton-cg:也是牛顿法家族的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
-
sag:即随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度,适合于样本数据多的时候。
-
saga:线性收敛的随机优化算法的的变种.
liblinear适用于小数据集,而sag和saga适用于大数据集因为速度更快;对于多分类问题,只有newton-cg,sag,saga和lbfgs能够处理多项损失;newton-cg,sag和lbfgs这三种优化算法时都需要损失函数的一阶或者二阶连续导数,因此不能用于没有连续导数的L1正则化,只能用于L2正则化。而liblinear和saga 在L1正则化和L2正则化时通用。但这几个算法在应用到多分类时,也会有不同的限制。
[max_iter] 算法收敛最大迭代次数,int类型,默认为10。仅在正则化优化算法为newton-cg, sag和lbfgs才有用,算法收敛的最大迭代次数。
[multi_class] 分类方式选择参数,str类型,可选参数为ovr和multinomial,默认为ovr。ovr即one-vs-rest(OvR),而multinomial即many-vs-many(MvM)。这个在多分类时需要考虑的参数,在此不详细展开。
[verbose] 日志冗长度,int类型。默认为0。就是不输出训练过程,1的时候偶尔输出结果,大于1,对于每个子模型都输出。
[warm_start] 热启动参数,bool类型。默认为False。如果为True,则下一次训练是以追加树的形式进行(重新使用上一次的调用作为初始化)。
[n_jobs] 并行数,int类型,默认为1。1的时候,用CPU的一个内核运行程序,2的时候,用CPU的2个内核运行程序。为-1的时候,用所有CPU的内核运行程序
五 总结
总之,逻辑回归是一个分类模型,虽然叫做“回归”。它本质上还是线性模型,其决策边界是线性函数。同时逻辑回归的代价函数极大值因为可以化为凸优化问题,所以求解还是比较方便。逻辑回归的优势在于对于需要高维度大量数据的情况下的工程效率很高,可用性强。
好了,我们今天的逻辑回归就介绍完了。祝大家节日快乐~ 在休假之余给我们的公众号提提意见,附带转转我们的文章,小编的节日就更快乐啦:)。
欢迎大家留言提建议,并关注我们的公众号。