数据结构-TREAP（拒绝旋转版）

吐槽

Treap=Tree+Heap
呜哇，调了两个多月终于成功了什么的。。
一直找不到板子A掉之后才发现板子到处都是TUT
所以即使代码丑也要写博客记录一下QWQ~

---

定义

Tree 　二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。具有以下性质：

1. 若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；
2. 若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；
3. 左、右子树也分别为二叉排序树；左、右子树也分别为二叉排序树；

Heap　 堆，堆中某个节点的值总是不大于或不小于其父节点的值；
Treap　树堆，在数据结构中也称Treap，是指有一个随机附加域满足堆的性质的二叉搜索树，其结构相当于以随机数据插入的二叉搜索树。其基本操作的期望时间复杂度为O(logn)。相对于其他的平衡二叉搜索树，Treap的特点是实现简单，且能基本实现随机平衡的结构。

---

思想

Treap维护堆性质的方法用到了旋转，然而作者太弱了，并不能鱼块地转来转去，就去学习了非旋转维护堆的性质的方法QWQ~

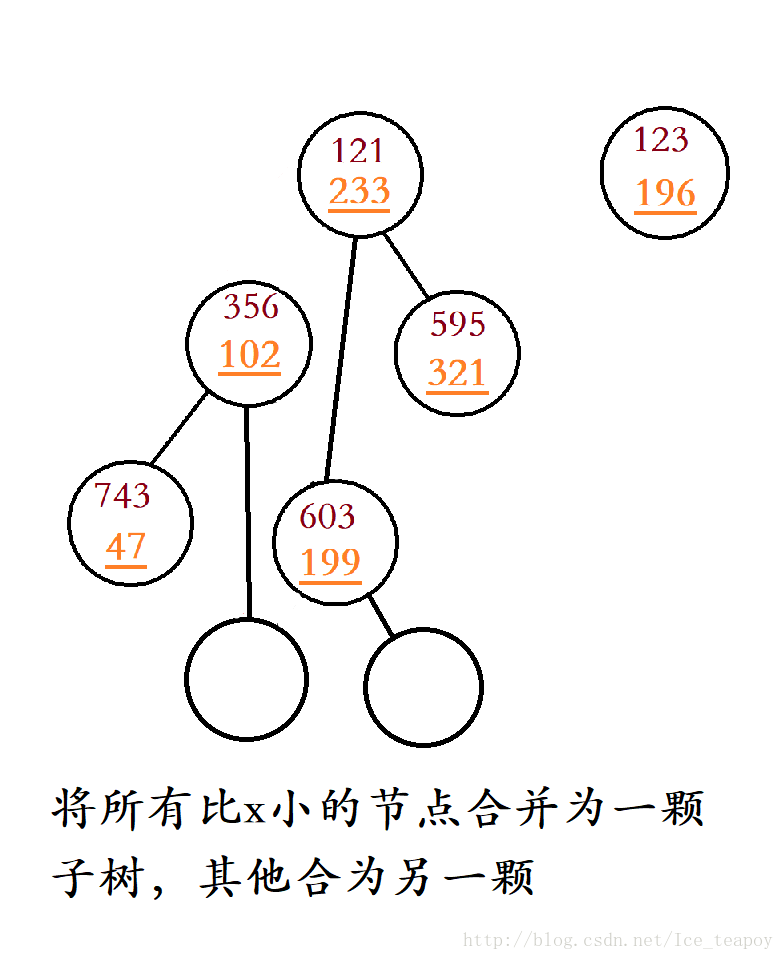
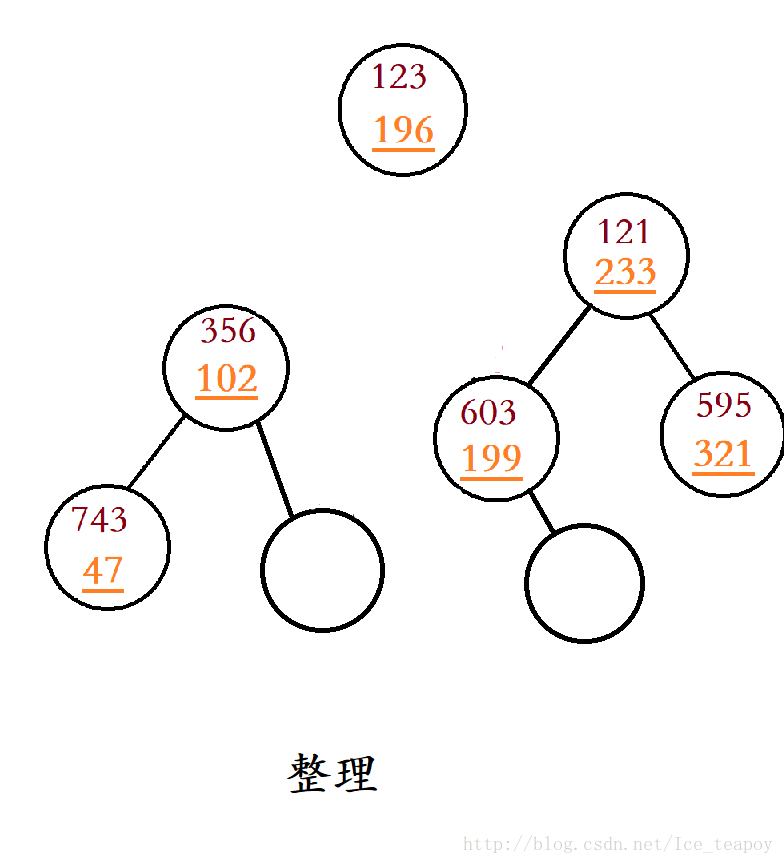
主要思想就是拆分和合并。

拆分操作是要将平衡树拆分成一颗所有元素均大于x的平衡树和一颗所有元素均小于等于x的平衡树 ；合并操作是将两颗平衡树合并成一颗。

---

过程

---

例题

题目地址：https://www.luogu.org/problemnew/show/P3369

#include 
#include 
#include 
#include 
using namespace std;

struct qwq//在此起pair的作用，然而不会stl什么的QWQ。。。 
{
	int p1,p2;
}o,q;

qwq QWQ(int x,int y)//make_pair 
{
	o.p1=x;
	o.p2=y;
	return o;
}

struct asdf//存树每个节点的左儿子，右儿子，该节点子树的大小，值，平衡种子 
{
	int l,r,size,c,key;
}tree[100001];
int n,g,m;//操作数，平衡树的根，指针 
int sum;

qwq chaifen(int p,int x)//将树拆分成一颗所有元素均大于x的树和一颗所有元素均小于等于x的树 
{
	if (p==0) return QWQ(0,0);//空树被拆分成两颗空树 
	if (tree[p].c>tree[x].c)//该平衡子树的根比x大，则说明该节点右子树中所有节点均比x大
	{
	    tree[p].size-=tree[tree[p].l].size;//将其左子树拆分成一颗所有元素均大于x的平衡树和一颗所有元素均小于等于x的平衡树
		tree[p].l=q.p2;//并将其左子树拆分出的大于x的平衡子树作为p的左儿子
		tree[p].size+=tree[tree[p].l].size;
		return QWQ(q.p1,p);
	}//反之相同 
	tree[p].size-=tree[tree[p].r].size;
	q=chaifen(tree[p].r,x);
	tree[p].r=q.p1;
	tree[p].size+=tree[tree[p].r].size;
	return QWQ(p,q.p2);
}

int hebing(int pf,int pl) 
{//由于拆分函数的性质，pf中所有元素均小于pl 
	if (pf==0) return pl;
	if (pl==0) return pf;
	if (tree[pf].key>tree[pl].key)//根据堆的性质决定元素深度，根据二叉搜索树的性质决定左右 
	{
		tree[pl].size+=tree[pf].size;
		tree[pl].l=hebing(pf,tree[pl].l);
		return pl;
	}
	tree[pf].size+=tree[pl].size;
	tree[pf].r=hebing(tree[pf].r,pl);
	return pf;
}

//插入 
{
	q=chaifen(g,x);
	//将树拆分成一颗所有元素均大于x的平衡树和一颗所有元素均小于x的平衡树 
	g=hebing(hebing(q.p1,x),q.p2);//将三颗平衡树合并 
}

int find(int p,int k)
{
	if (tree[tree[p].l].size+1==k) return tree[p].c;
	if (tree[tree[p].l].size>=k) return find(tree[p].l,k);
	return find(tree[p].r,k-tree[tree[p].l].size-1);
}

int geshu1(int p,int x)//求比x小的元素个数 
{
	if (!p) return sum;//p为空树，不能继续寻找下去 
	if (tree[p].c>=x)//若p大于等于x，则p的右子树均大于等于x，访问p的左子树 
	{
		geshu1(tree[p].l,x);
	    return sum;
	}//若p小于x，则p的左子树均小于x，访问p的右子树 
	sum+=tree[tree[p].l].size+1;
	geshu1(tree[p].r,x);
	return sum;
}

int geshu2(int p,int x)//求小于等于x的元素个数，与上同 
{
	if (!p) return sum;
	if (tree[p].c>x)
	{
		geshu2(tree[p].l,x);
	    return sum;
	}
	sum+=tree[tree[p].l].size+1;
	geshu2(tree[p].r,x);
	return sum;
}

int dele(int p,int x)//删除元素和拆分思想一致，即将原树拆成一颗等于x的树和另一颗树 
{
	if (!p) return 0; 
	if (tree[p].c==x) return hebing(tree[p].l,tree[p].r);
	if (tree[p].c>x)
	{
		tree[p].size-=tree[tree[p].l].size;
		tree[p].l=dele(tree[p].l,x);
		tree[p].size+=tree[tree[p].l].size;
	}
	else
	{
		tree[p].size-=tree[tree[p].r].size;
		tree[p].r=dele(tree[p].r,x);
		tree[p].size+=tree[tree[p].r].size;
	}
    return p;
}

int main()
{
	scanf("%d",&n);
	int TT,xx;
	for (int i=1;i<=n;++i)
	{
		sum=0;
		scanf("%d%d",&TT,&xx);
		if (TT==1)//插入x数
		{
			tree[++m].c=xx;
			tree[m].key=rand()%2147483647;
			tree[m].size=1;
			charu(m);
		}
		if (TT==2) g=dele(g,xx);//删除x数(若有多个相同的数，因只删除一个)
		if (TT==3) printf("%d\n",geshu1(g,xx)+1);//查询x数的排名(排名定义为比当前数小的数的个数+1。若有多个相同的数，因输出最小的排名)
		if (TT==4) printf("%d\n",find(g,xx));//查询排名为x的数
		if (TT==5) printf("%d\n",find(g,geshu1(g,xx)));//求x的前驱(前驱定义为小于x，且最大的数)
		if (TT==6) printf("%d\n",find(g,geshu2(g,xx)+1));//求x的后继(后继定义为大于x，且最小的数)
	}
}