三种工具绘制errorbar图

 

误差棒是数据可变性的图形表示，并用于图表以指示所报告的测量中的误差或不确定性。他们给出了测量精确度的一般概念，或者相反，距报告值有多远，真实（无误差）值可能是多少。误差线通常代表不确定度的一个标准偏差，一个标准误差或特定的置信区间（例如95％间隔）。

如果各种其他条件成立，误差棒可以用来比较两种数量。这可以确定差异是否具有统计显着性。误差条也可以表明给定函数的拟合度，即函数描述数据的程度。实验科学中的科学论文预计在所有图表中都包含误差线。也已经表明，误差条可以被用作用于控制近似计算的概率算法的直接操纵界面。误差线也可以用正负号（±）加上误差的上限和减去误差的下限来表示。

在论文写作中，经常会用到数据图表示一组数据的特点，可视化的图形能够十分清楚直观的比较数据之间的差异。对于数据的均值和标准差在同一个图中表示，可以很好的比较数据分布的差异，errorbar便是这么一种图。

1、Excel画图

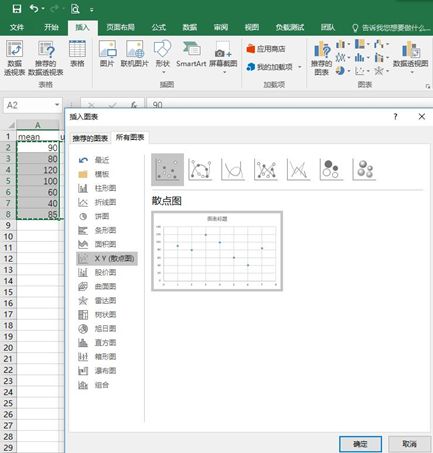
（1）首先，选择一组数据，包含均值和标准差。

（2）选择数据，然后在菜单栏插入——所有图表——散点图，点击确定

（3）选择图表右上角+号标记，选择误差线，并且选择误差数据即可。

 

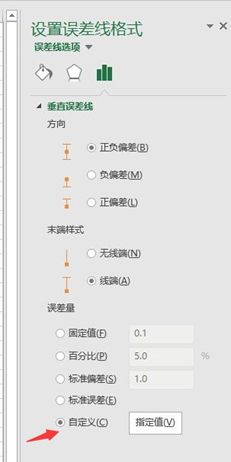
4）点击更多选项，可以设置误差线的格式。如正负偏差，末端样式和自定义误差数据，上下限可以不同。

 

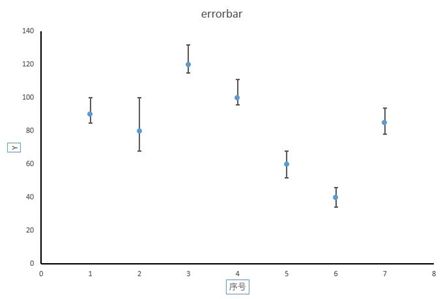
（5）结果如图所示

2、origin 画图

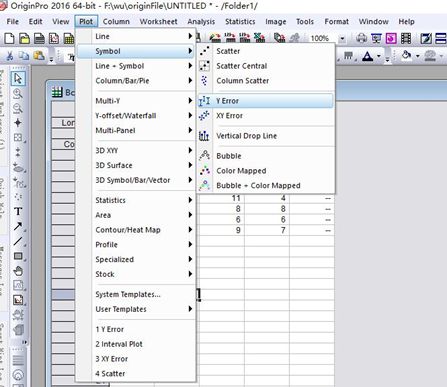
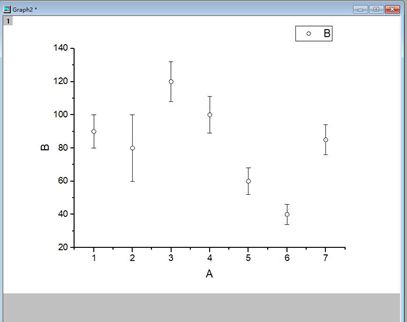
（1）选择数据，在菜单栏plot——symbol——Y Error

 

（2）图如下所示。可以设置线型样式，标记样式等

 

3、matlab 画图

（1）matlab画图函数为errorbar，函数调用方式如下所示几种

 

 

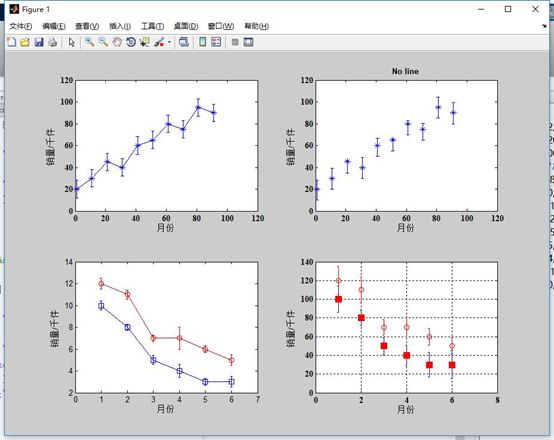
（2）matlab函数绘制的几种errorbar图形

（3）代码实例

三种工具绘制errorbar图 误差棒是数据可变性的图形表示，并用于图表以指示所报告的测量中的误差或不确定性。他们给出了测量精确度的一般概念，或者相反，距报告值有多远，真实（无误差）值可能是多少。误差线通常代表不确定度的一个标准偏差，一个标准误差或特定的置信区间（例如95％间隔）。 如果各种其他条件成立，误差棒可以用来比较两种数量。这可以确定差异是否具有统计显着性。误差条也可以表明给定函数的拟合度，即函数描述数据的程度。实验科学中的科学论文预计在所有图表中都包含误差线。也已经表明，误差条可以被用作用于控制近似计算的概率算法的直接操纵界面。误差线也可以用正负号（±）加上误差的上限和减去误差的下限来表示。 在论文写作中，经常会用到数据图表示一组数据的特点，可视化的图形能够十分清楚直观的比较数据之间的差异。对于数据的均值和标准差在同一个图中表示，可以很好的比较数据分布的差异，errorbar便是这么一种图。 1、Excel画图 （1）首先，选择一组数据，包含均值和标准差。 （2）选择数据，然后在菜单栏插入——所有图表——散点图，点击确定 （3）选择图表右上角+号标记，选择误差线，并且选择误差数据即可。   4）点击更多选项，可以设置误差线的格式。如正负偏差，末端样式和自定义误差数据，上下限可以不同。   （5）结果如图所示 2、origin 画图 （1）选择数据，在菜单栏plot——symbol——Y Error   （2）图如下所示。可以设置线型样式，标记样式等   3、matlab 画图 （1）matlab画图函数为errorbar，函数调用方式如下所示几种     （2）matlab函数绘制的几种errorbar图形 （3）代码实例   ? 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 %errorbar函数实例 figure; subplot(2,2,1); %横轴 x = 1:10:100; %均值 y = [20 30 45 40 60 65 80 75 95 90]; %标准差 err = 8*ones(size(y)); %线型，颜色，线宽，标记大小 errorbar(x,y,err,'-*b','LineWidth',1','MarkerSize',8)  xlabel('月份');ylabel('销量/千件'); %设置坐标轴字体大小粗细，字体样式以及横纵轴范围 set(gca,'fontsize',10,'fontweight','bold','FontName','Times New Roman','XLim',[0,120],'YLim',[0,120]);    subplot(2,2,2); x = 1:10:100; y = [20 30 45 40 60 65 80 75 95 90]; err1 = 10*ones(size(y)); err2 = 10*rand(size(y)); errorbar(x,y,err1,err2,'*b','LineWidth',1','MarkerSize',8)  xlabel('月份');ylabel('销量/千件'); title('No line','fontsize',10,'fontweight','bold'); %设置坐标轴字体大小粗细，字体样式以及横纵轴范围 set(gca,'fontsize',10,'fontweight','bold','FontName','Times New Roman','XLim',[0,120],'YLim',[0,120]);   subplot(2,2,3) Average1=[12,11,7,7,6,5]; Variance1=[0.5,0.4,0.3,1,0.3,0.5];     %A地的数据 Average2=[10,8,5,4,3,3]; Variance2=[0.4,0.3,0.4,0.6,0.3,0.5];    %B地的数据 Time=1:1:6; errorbar(Time,Average1,Variance1,'r-o')    %A地误差棒图，用红色线表示 hold on errorbar(Time,Average2,Variance2,'b-s')    %B地误差棒图，用蓝色线表示 xlabel('月份');ylabel('销量/千件');   subplot(2,2,4); Average2=[120,110,70,70,60,50]; Variance2=[15,14,8,10,9,9];     %A地的数据 Average3=[100,80,50,40,30,30]; Variance3=[14,8.3,9.4,10.6,13,15];    %B地的数据 Time=1:1:6; errorbar(Time,Average2,Variance2,'ro')    %A地误差棒图，用红色线表示 hold on errorbar(Time,Average3,Variance3,'bs','MarkerSize',10,...     'MarkerEdgeColor','red','MarkerFaceColor','red')    %B地误差棒图，用蓝色线表示 xlabel('月份');ylabel('销量/千件'); set(gca,'fontsize',10,'fontweight','bold','FontName','Times New Roman','XLim',[0,8],'YLim',[0,140]); grid on;