凸包 graham 算法

向量：

1.向量的内积（数量积，点乘）：

公式：a· b = |a| * |b| cos＝a.x* b.y + b.x * a.y

2.向量的外积（向量积，差乘）：

公式：|c|= |a|*|b|*sin = a.x * b.y - b.x * a.y

意义：

1).两个向量和坐标原点所围成的面积（可正可负）。

2).值为正值表示向量a在向量b的顺时针方向,反之,向量a在向量b的逆时针方向,相等时,共线.

凸包:由平面上的最小点所围成的多边形,平面上任何其它的点都在这个多边形内部，这个多边形就称为

凸包。

                                         (图1) 

graham算法：

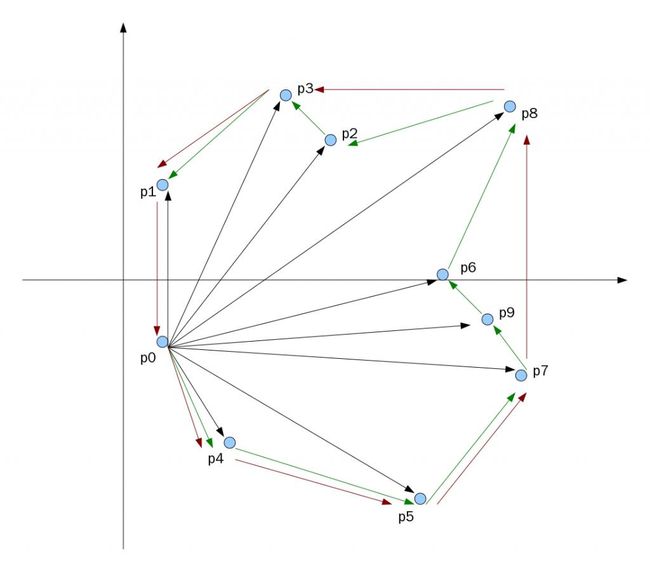
第一步:选取x轴坐标最小的点,如果存在多个选y轴坐标最小的点.(如图1,p0点)

第二步:排序.从下到上扫描有其它点.(如图1)扫描的结果顺序,p0, p4, p5, p7, p9,p6, p8, p2,p3, p1.

数学公式向量的外积模公式:|c|(是模不是绝对值符号)= |a|*|b|*sin = a.x * b.y – b.x * a.y

|c|> 0:向量a在向量b的顺时针方向,因为此例原点坐标取x轴坐标最小的点,所以,向量a在向

量b的下方.(p0-p4线段在p0-p5的下方).

|c|= 0:共线时,按照与原点距离由小到大的顺序.

第三步:按照第二步得到的顶点顺序进行graham扫描.按照本例选取的原点方式,当扫描到左拐(p0,p4, p5)时保留(p4),右拐(p9,p6, p8)时删除顶点(p6),结果就是凸包的顶点集.(绿线扫描的顺序，红线为左拐点).共线时,删除距离较小的点.

注意：右拐删除结点时,必须回溯与前面保留的点重新比较,因为删除一个点后先前拐点性质会发生变化

例如:删除p6后,(p7, p9, p8) 也是右拐了.

所谓的左拐/右拐就沿着边界扫描后,其它的点是否在当前点与下一点连线与原点的内部.

例如:结果p7-p8是凸包的顶点,p7-p8直线会把所有其它点挡在原点p0方向的一侧.

数学公式:

向量外积模公式

例:

p5– p4向量Xp0 – p4 向量>0, (p5–p4)在(p0–p4)的顺时针方向,左拐

p8– p6向量Xp9 – p6向量<0, (p8–p6)在(p9–p6)的逆时针方向,右拐

也可以采用其它向量方式

例:

p4–p0向量Xp5–p0向量>0, (p4–p0)在(p5–p0)的顺时针方向,左拐

p6–p9向量Xp8–p9向量<0, (p6–p9)在(p8–p9)的逆时针方向,右拐

示例程序:

p0:(1, -2)

p1:(1, 2)

p2:(5, 3)

p3:(4,5)

p4:(2, -4)

p5:(6, -6)

p6:(7, 0)

p7:(10, -3)

p8:(9, 4)

p9:(8, -1)

input:

10

1 -2

1 2

5 3

4 5

2 -4

6 -6

7 0

10-3

9 4

8 -1

output:

1 -2

2 -4

6 -6

10-3

9 4

4 5

1 2

源代码:

#include
#include
#include
#include

#define MAX_NUMS 10

typedef struct
{
    int x;
    int y;
} veritice;

veritice   vet[MAX_NUMS];
int                   n;
std::vector  v;

inline int cross(const veritice& p0, const veritice& p1, const veritice& p2)
{
    veritice u, v;

    u.x = p1.x - p0.x, u.y = p1.y - p0.y;
    v.x = p2.x - p0.x, v.y = p2.y - p0.y;

    return v.x * u.y - u.x * v.y;
}

inline int distance(const veritice& p1, const veritice& p2)
{
    return (p2.x - p1.x) * (p2.x - p1.x) + (p2.y - p1.y) * (p2.y - p1.y);
}

inline int graham_compare(const void* a, const void* b)
{
    int result = cross(vet[0], *(veritice*)a, *(veritice*)b);

    if(result)
        return result;

    return distance(vet[0], *(veritice*)a) - distance(vet[0], *(veritice*)b);
}

inline void graham_scan()
{
    v.push_back(vet[0]);
    v.push_back(vet[1]);

    for(int i = 2; i < n; i++)
    {
        while( cross(v[v.size() - 1], v[v.size() - 2], vet[i]) <= 0)
            v.pop_back();

        v.push_back(vet[i]);
    }
}

int main()
{
    std::ifstream in("case_in");
    int index = 0;

    in >> n;

    for(int i = 0; i < n; i++)
    {
        in >> vet[i].x >> vet[i].y;

        if(vet[0].x > vet[i].x || (vet[0].x == vet[i].x && vet[0].y > vet[i].y))
            index = i;
    }

    in.close();
// 第一步
    veritice temp;
    temp.x       = vet[0].x,       temp.y       = vet[0].y;
    vet[0].x     = vet[index].x,   vet[0].y     = vet[index].y;
    vet[index].x = temp.x,         vet[index].y = temp.y;

// 第二步
    qsort(vet + 1, n - 1, sizeof(veritice), graham_compare);

//　第三步
    graham_scan();

//  输出
    for(unsigned int i = 0; i < v.size(); i++)
        std::cout << v[i].x << ' ' << v[i].y << std::endl;

    return 0;
}