二叉树之先序遍历（递归和非递归两种遍历）

二叉树是每个节点最多有两个子节点的有序树。二叉树常被用作二叉查找树和二叉堆或是二叉排序树。

二叉树的第i层至多有2^(i -1)个节点；

深度为k的二叉树至多有2^k - 1个节点；

对任何一颗二叉树，若其终端节点数为n0,度为2的节点数为n2,则 n0 = n2 + 1;

------------------------------------------------------------------------------------------------------------------------------------------------------------

二叉树的先序遍历：顾名思义，先访问根节点，再访问左节点，最后访问右节点。先序遍历的特点需要使用到栈这种先进后出的数据结构。

首先还是定义二叉树这种链式存储结构的结构体：

typedef struct BiTNode{
char data;
struct BiTNode* lchild, *rchild;
}BiTNode, *BiTree;

创建二叉树的过程：

void  CreateBiTree(BiTree  &T)  // 创建二叉树
{
char data;
    scanf("%c", &data);
    if(data == '#'){       // '#'表示空节点 
          T = NULL; 
     } 
    else
{ 
T = (BiTree)malloc(sizeof(BiTNode));
    T->data = data;
    CreateBiTree(T->lchild);
    CreateBiTree(T->rchild);
    }
}

------------------------------------------------------------------------------------------------------------------------------------------------------------

递归遍历是最容易理解的：

void visit(BiTree T)         // 输出
{
   if(T->data!= '#')
    {
   cout<data<<" ";
    }
}

void  PreOrder(BiTree T)     // 先序递归遍历
{
 if(T != NULL)
 {
  visit(T);            // 访问根节点
  PreOrder(T->lchild); // 访问左孩子
  PreOrder(T->rchild); // 访问右孩子
 }
}

////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

非递归遍历：

就跟着先序遍历定义来，（一个用于遍历的节点Node, 一个用于存储的结构栈）

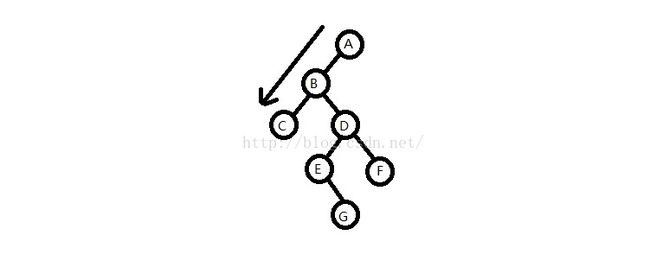
1.输出根节点，根节点入栈，从上而下遍历到最下面的那个左孩子节点B（相对于根节点而言），分别入栈，然后输出；（除了叶子节点以外，其余的都可以当作根节点）

如图箭头所指的即为第一步完成的。

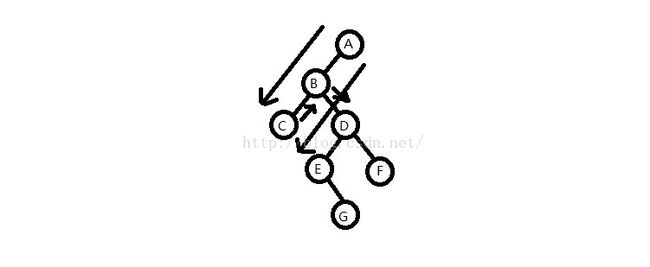
2.把栈顶元素赋给遍历的节点Node,然后出栈，从下往上的把该遍历的节点Node的右孩子节点赋给Node。

 

分析过程：

依照上图，即把节点C赋给这个遍历的贯穿的节点Node，让其出栈，没有右孩子节点，即Node为NULL；

然后回到步骤1，Node为NULL不执行，继续步骤2，即把B赋给Node,然后出栈，B有右节点D,D赋给Node,

再回到步骤1，如图：第二个从上往下指的箭头（DE旁边的那条）

如此往复，最终当队列为空，遍历用的节点Node也为空了也就遍历完成了。

 

程序代码：

#include
#include
using namespace std;

typedef struct BiTNode{
 char data;
 BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

void CreateBiTree(BiTree& T)            // 创建二叉树
{
 char data;
 cin>>data;
 if(data == '#')                    // # 表示为空节点，也作为递归的结束标志
 {
  T = NULL;
 }
 else
 {
  T = (BiTree)malloc(sizeof(BiTNode));
  T->data = data;
  CreateBiTree(T->lchild);
     CreateBiTree(T->rchild);
 }
}

void PreOrder(BiTree T)                // 先序遍历非递归
{
 BiTree B = T;                    // 用于遍历的节点
 stack s;
 
 while(B != NULL || !s.empty())
 {
  while(B)
  {
   cout<data<<" ";
   s.push(B);
   B = B->lchild;
  }
  if(!s.empty())
  {
   B = s.top();
   s.pop();
   B = B->rchild;
  }
  
 }
}
int main()
{
 BiTree T;
 CreateBiTree(T);
 PreOrder(T);
 system("pause");
 return 0;
}