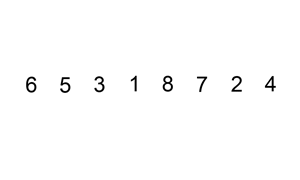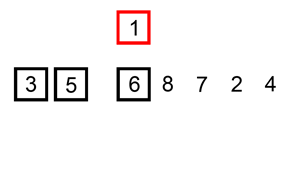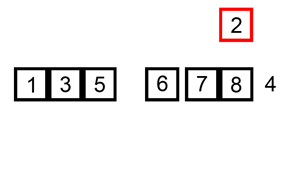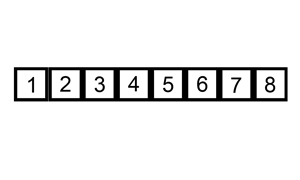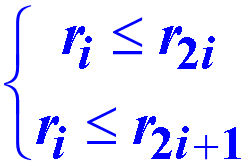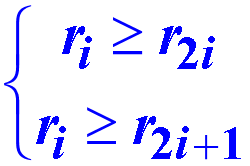几种排序知识讲解

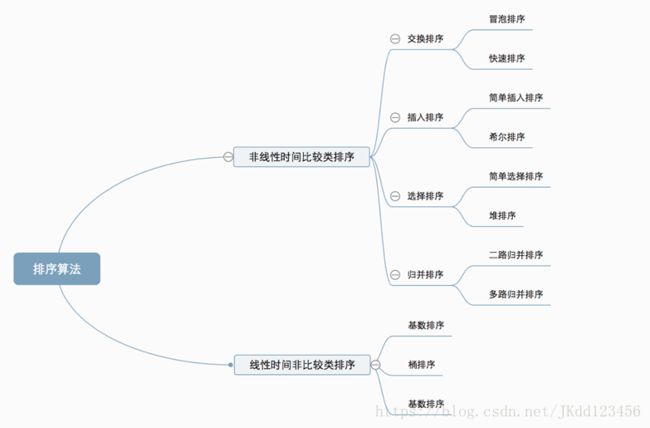
一：几种排序方法 

 

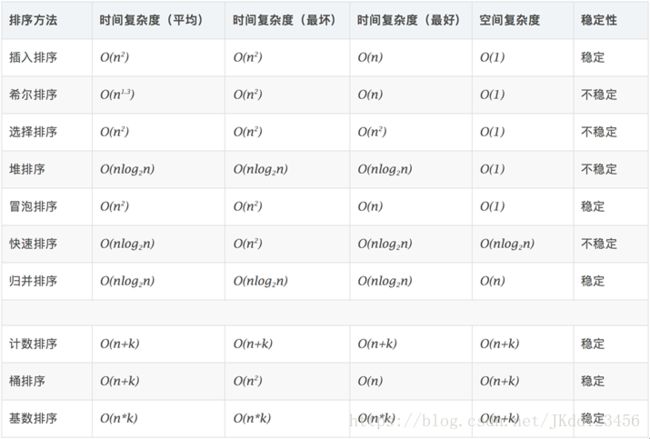
排序算法的复杂度： 

 

ACM常用算法排序

 

二、

1、冒泡排序：

冒泡排序是一种简单的排序算法，但是时间复杂度较大。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

：算法描述

（1）、比较相邻的元素。如果第一个比第二个大，就交换它们两个；

（2）、对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；

（3）、针对所有的元素重复以上的步骤，除了最后一个；

（4）、重复步骤1~3，直到排序完成。

3：动画演示

4：核心CODE:

int BubbleSort(int arr[],int len) {
    for (int i = 0; i < len - 1; i++) {
        for (int j = 0; j < len - 1 - i; j++) {
            if (arr[j] > arr[j+1]) {        // 相邻元素两两对比
                int temp = arr[j+1];        // 元素交换
                arr[j+1] = arr[j];
                arr[j] = temp;
            }
        }
    }
    return arr;
}

 

三、

1：选择排序：

选择排序(Selection-sort)是一种简单直观的排序算法。

用 pos 变量记录位置，每次在找完最小（大）元素之后与 pos 位置的元素交换

它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

2：算法描述

（1）、初始状态：无序区为R[1..n]，有序区为空；

（2）、第i趟排序(i=1,2,3…n-1)开始时，当前有序区和无序区分别为R[1..i-1]和R(i..n）。该趟排序从当前无序区中-选出关键字最                 小的记录 R[k]，将它与无序区的第1个记录R交换，使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减               少1个的新无序区；

（3）、 n-1趟结束，数组有序化了。

3：动画演示

4：核心CODE:

int  selectionSort(int arr[], int len) {
    int minIndex, temp;
    for (int i = 0; i < len - 1; i++) {
        minIndex = i;
        for (int j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {     // 寻找最小的数
                minIndex = j;                 // 将最小数的索引保存
            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    return arr;
} 

 

四：
1：插入排序

插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

2：算法描述

（1）、从第一个元素开始，该元素可以认为已经被排序；

（2）、取出下一个元素，在已经排序的元素序列中从后向前扫描；

（3）、如果该元素（已排序）大于新元素，将该元素移到下一位置；

（4）、重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；

（5）、将新元素插入到该位置后；

（6）、重复步骤2~5。

 

3：动画演示

4：核心CODE：

int  insertionSort(int arr[] ,int len) {
    int preIndex, current;
    for (int i = 1; i < len; i++) {
        preIndex = i - 1;
        current = arr[i];
        while (preIndex >= 0 && arr[preIndex] > current) {
            arr[preIndex + 1] = arr[preIndex];
            preIndex--;
        }
        arr[preIndex + 1] = current;
    }
    return arr;
}

 

五： 

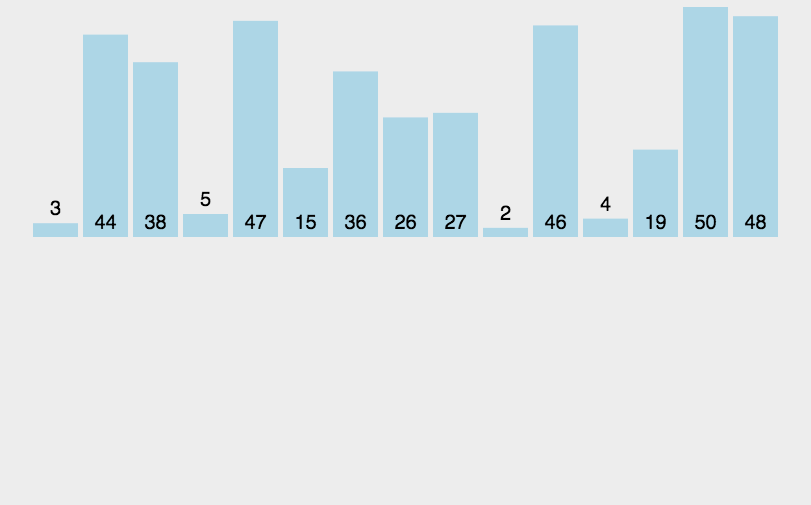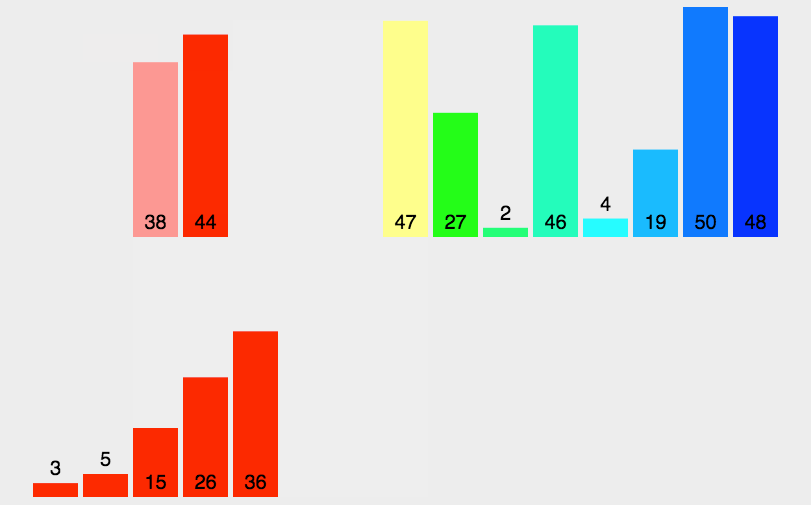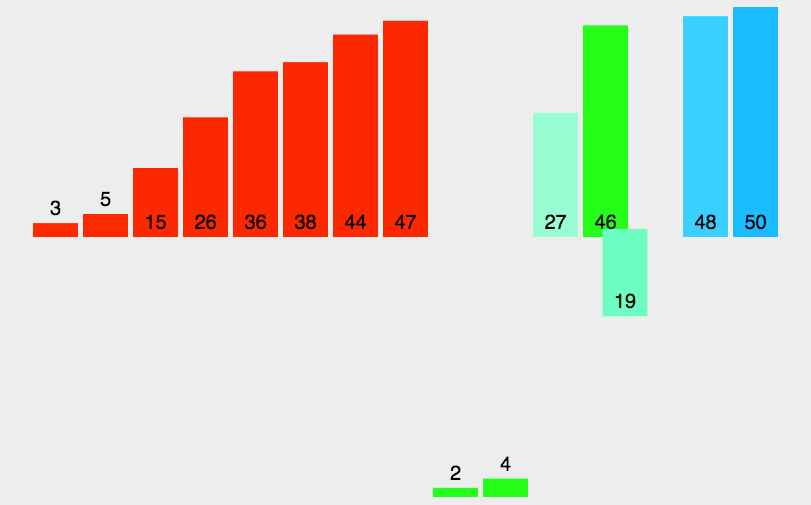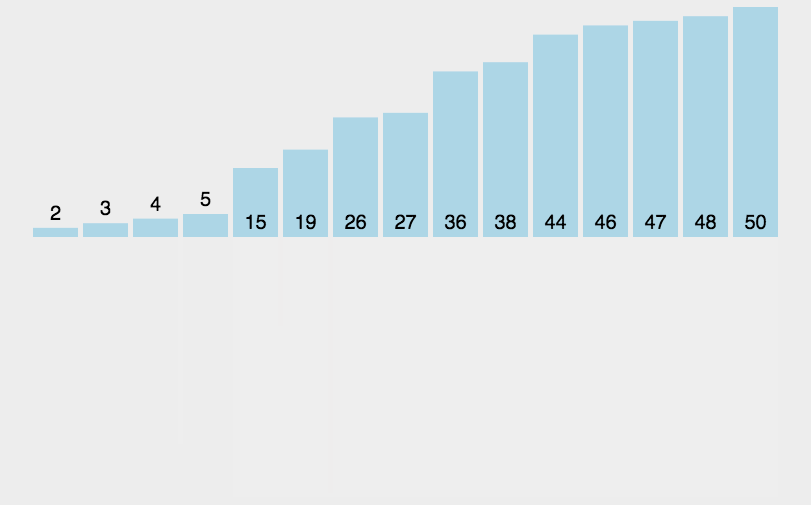
1：合并排序（归并排序）

合并操作(merge)，是采用分治法（Divide and Conquer）的一个非常典型的应用。

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

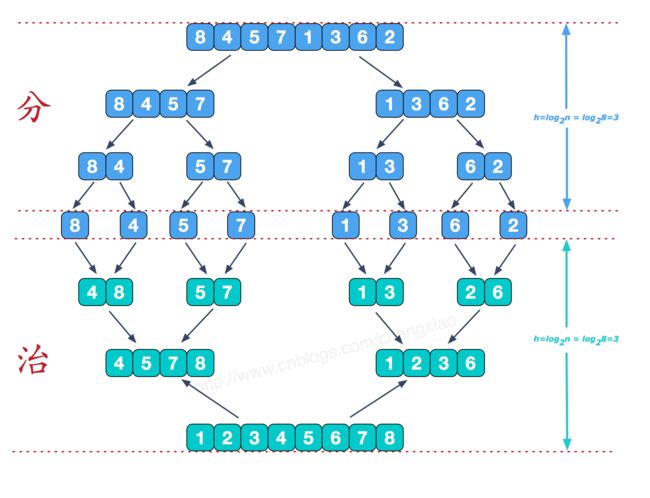
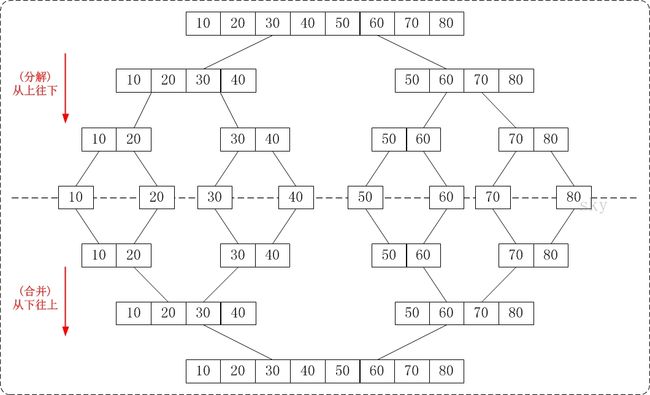
合并排序组主要是两个步骤：  分  +  治（合并）

 

2：算法描述

（1）、把长度为n的输入序列分成两个长度为n/2的子序列；

（2）、对这两个子序列分别采用归并排序；

（3）、将两个排序好的子序列合并成一个最终的排序序列。

 

归并排序采用的是递归的方式，每次对区间进行递归，每个区间又可以分为左右区间，执行完左区间之后，执行右区间

---

 

3：动画演示

 

4：核心CODE：

//  b数组作为临时数组，当比较的时候，存放值

void Merge(LL first,LL mid,LL last)
{
    LL be=first;
    LL en=mid;
    LL be1=mid+1;
    LL en1=last;
    LL flag=0;

    while(be<=en&&be1<=en1)
    {
        if(a[be]<=a[be1])
            b[flag++]=a[be++];
        else
        {
            b[flag++]=a[be1++];
        }
    }

    if(be<=en)
    {
        for(LL i=be;i<=en;i++)
            b[flag++]=a[i];
    }

    if(be1<=en1)
    {
        for(LL i=be1;i<=en1;i++)
            b[flag++]=a[i];
    }

    for(LL i=0;i

 

六：

1、快速排序

快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

2：算法描述

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：
（1）、从数列中挑出一个元素，称为 “基准”（pivot），一般是第一个元素；
（2）、重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面

（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
（3）、递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

 

3：

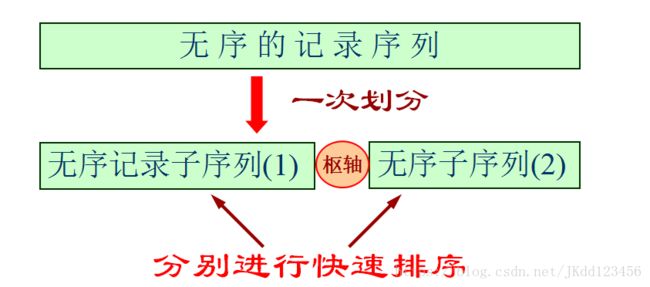
一趟快速排序（一次划分）

目标：找一个记录，以它的关键字作为“枢轴”，凡其关键字小于枢轴的记录均移动至该记录之前，反之，凡关键字大于枢轴的记录均移动至该记录之后。

致使一趟排序之后，记录的无序序列R[s..t]将分割成两部分：R[s..i-1] 和 R[i+1..t],    R[j]≤ R[i] ≤ R[j]    (s≤j≤i-1)    枢轴     (i+1≤j≤t)

 

首先对无序的记录序列进行“一次划分”，之后分别对分割所得两个子序列“递归”进行快速排序。

 

例如：

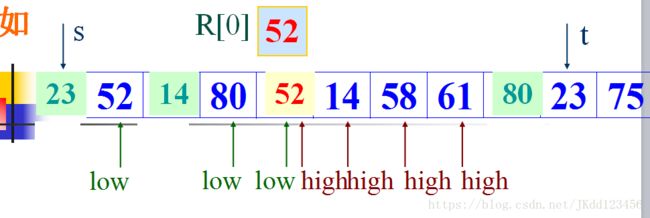
设 R[s]=52 为枢轴暂存在R[0]的位置上 

将 R[high] 和 枢轴的关键字进行比较，要求R[high] ≥ 枢轴的关键字
将 R[low] 和 枢轴的关键字进行比较，要求R[low]≤ 枢轴的关键字

 

可见，经过“一次划分” ，将关键字序      52, 49, 80, 36, 14,  58, 61, 97, 23, 75 
调整为:  23, 49, 14, 36, (52) 58, 61, 97, 80, 75

在调整过程中，设立了两个指针: low 和high，它们的初值分别为: s 和 t, 之后逐渐减小 high，增加 low，并保证
R[high]≥52，和  R[low]≤52,否则进行记录的“交换”。

 

4：动画描述

 

5：核心CODE：

进行分区操作

int partition(int low,int high)
{
    a[0]=a[low];
    pivotker=a[low];
    
    while(low=pivotkey)
            --high;  
        a[low]=a[high];
        
        while(low

 

七、堆排序

1：堆排序

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

2：算法描述

（1）、将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆或者小顶堆，此堆为初始的无序区；
（2）、将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),

且满足R[1,2…n-1]<=R[n]；
（3）、由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

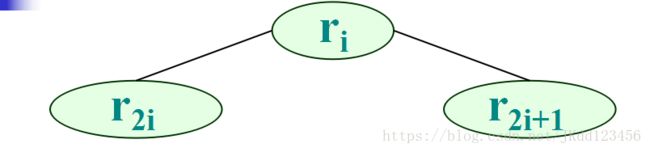
堆是满足下列性质的数列{r1, r2, …，rn}：

小顶堆

大顶堆

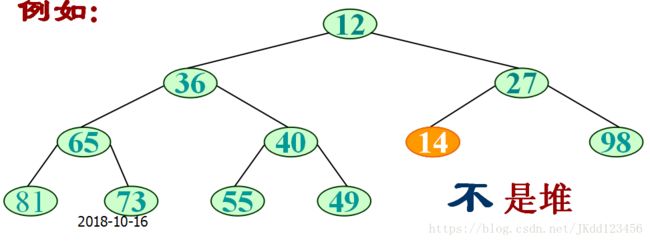
例如

{12, 36, 27, 65, 40, 34, 98, 81, 73, 55, 49}       是小顶堆

{12, 36, 27, 65, 40, 14, 98, 81, 73, 55, 49}       不是堆
 

3：若将该数列视作完全二叉树，
则 r2i 是 ri 的左孩子; r2i+1 是 ri 的右孩子。

4：动画演示

5：

堆排序即是利用 堆 的特性对记录序列进行排序的一种排序方法。 

6:

定义堆的类型：

typedef  SqList HeapType;
     // 堆采用顺序表表示

两个问题：

如何筛选？     如何建堆？

(1)、

所谓“筛选”指的是，对一棵左/右子树 均为堆的完全二叉树，“调整”根结点使整个二叉树也成为一个堆。

（2）、

建堆是一个从下往上进行“筛选”的过程