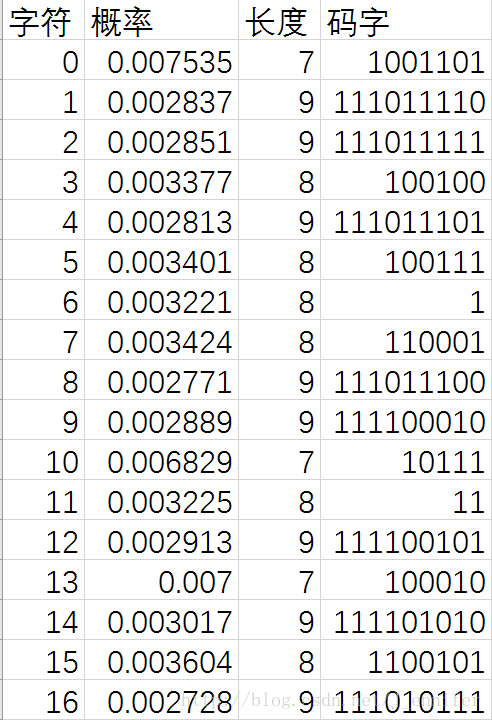
实验三：Huffman编码

一、 实验原理

Huffman于1952年提出了一种构造最佳码的方法，称为Huffman码。它利用了信源概率分布的特性进行编码，是一种最佳的逐个符号的编码方法。二元Huffman码的编码方法如下：
(1)将所有信源符号按照概率分布的大小，以递增的次序排列；
(2)用0和1码符号分别分配给概率最小的两个信源符号，并将这两个符号合并成一个新符号，其概率之和作为新符号的概率；
(3)将步骤(2)得到的新符号和剩余信源符号，重新按照概率分布大小以递增次序排列，再将两个概率最小的符号合并成新符号，并分别用0和1码表示；
(4)重复步骤(3)，直至最后剩下两个符号，其概率之和为1。将最后两个新符号分别用0和1码表示。从这两个符号开始，依照编码路径由上向下返回，得出各信源符号对应的码字。
在程序中需要通过二叉树结构实现Huffman算法。树上的每个节点都是一个结构体，由父节点、左子节点和右子节点三个基本元素构成。

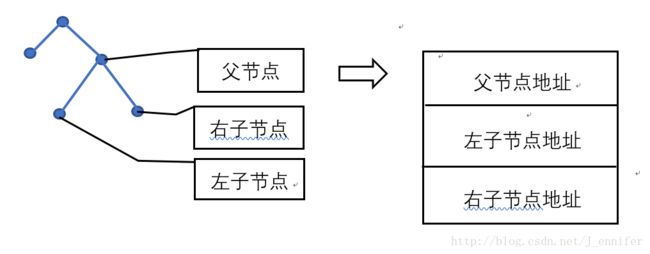
节点有两种类型：①树叶节点->对应一个码字->没有孩子 ②中间节点->不产生码字->有孩子

二、 实验步骤

本次实验需要建立两个工程文件，分别运行主程序和库程序；每个程序中都要包含头文件。

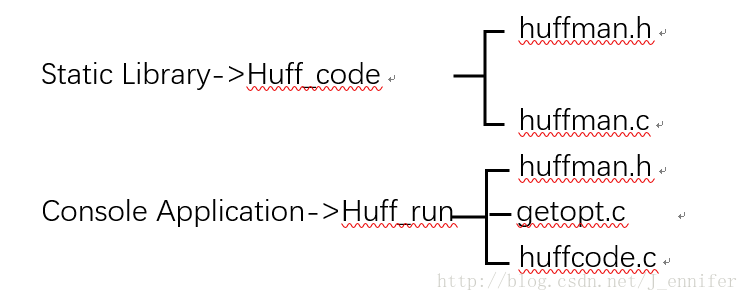
下面对老师所给程序进行分析。

1.huffman.h

#ifndef HUFFMAN_HUFFMAN_H
#define HUFFMAN_HUFFMAN_H

#include 

int huffman_encode_file(FILE *in, FILE *out);//文件编码函数，是本次实验的目标函数
int huffman_decode_file(FILE *in, FILE *out);//文件解码函数
int huffman_encode_memory(const unsigned char *bufin,
                          unsigned int bufinlen,
                          unsigned char **pbufout,
                          unsigned int *pbufoutlen);//内存编码函数
int huffman_decode_memory(const unsigned char *bufin,
                          unsigned int bufinlen,
                          unsigned char **bufout,
                          unsigned int *pbufoutlen);//内存解码函数
#endif

2.getopt.c

getopt()用来分析命令行参数。参数nargc和nargv是由main()传递的参数个数和内容。参数ostr则代表预处理选项字符串。getopt()设置的全局变量有：optarg-指向当前选项参数的指针；optind-再次调用getopt()时下一个argv指针的索引；optopt-最后一个未知选项。
在本次实验中，getopt()函数在huffcode.c文件中被调用。

int getopt(int nargc, char * const *nargv, const char* ostr)
{
    static char *place = EMSG;      /* option letter processing */
    char *oli;              /* option letter list index */

    if (optreset || !*place) {      /* update scanning pointer */
        optreset = 0;
        if (optind >= nargc || *(place = nargv[optind]) != '-') {
            place = EMSG;
            return (EOF);
        }
        if (place[1] && *++place == '-') {  /* found "--" */
            ++optind;
            place = EMSG;
            return (EOF);
        }
    }                   /* option letter okay? */
    if ((optopt = (int)*place++) == (int)':' ||
        !(oli = strchr(ostr, optopt))) {
        /*
         * if the user didn't specify '-' as an option,
         * assume it means EOF.
         */
        if (optopt == (int)'-')
            return (EOF);
        if (!*place)
            ++optind;
        if (opterr && *ostr != ':')
            (void)fprintf(stderr,
                "%s: illegal option -- %c\n", __FILE__, optopt);
        return (BADCH);
    }
    if (*++oli != ':') {            /* don't need argument */
        optarg = NULL;
        if (!*place)
            ++optind;
    }
    else {                  /* need an argument */
        if (*place)         /* no white space */
            optarg = place;
        else if (nargc <= ++optind) {   /* no arg */
            place = EMSG;
            if (*ostr == ':')
                return (BADARG);
            if (opterr)
                (void)fprintf(stderr,
                    "%s: option requires an argument -- %c\n",
                    __FILE__, optopt);
            return (BADCH);
        }
        else                /* white space */
            optarg = nargv[optind];
        place = EMSG;
        ++optind;
    }
    return (optopt);            /* dump back option letter */
}

3.huffcode.c

定义命令行参数：

static void
usage(FILE* out)
{
    fputs("Usage: huffcode [-i] [-o
] [-d|-c]\n"
          "-i - input file (default is standard input)\n"//输入文件名
          "-o - output file (default is standard output)\n"//输出文件名
          "-d - decompress\n"//解压缩
          "-c - compress (default)\n"//压缩
          "-m - read file into memory, compress, then write to file (not default)\n"//读取文件内存
          "-t - output statistics\n",//输出概率统计表
          out);
}//设置命令行参数

main()函数中对命令行的操作：

int
main(int argc, char** argv)//argc-参数个数，argv-参数内容
{
    char memory = 0;//memory缺省值为0，表示文件操作而非内存操作
    char compress = 1;//compress缺省值为1，表示解压缩
    int opt;//getopt()返回值，即命令行的参数选项或者-1
    const char *file_in = NULL, *file_out = NULL;
    const char *file_out_table = NULL;
    FILE *in = stdin;
    FILE *out = stdout;
    FILE * outTable = NULL;

    /* Get the command line arguments. */
    while((opt = getopt(argc, argv, "i:o:cdhvm")) != -1)
        /* 这里需要注意：不带值的参数可以连写，例如-1a或-a1；参数不分先后顺序；可选值的参数的值与参数之间不能有空格，必须写成-ddvalue这样的格式。*/
    {
        switch(opt)
        {
        case 'i':
            file_in = optarg;//-i，输入文件
            break;
        case 'o':
            file_out = optarg;//-o，输出文件
            break;
        case 'c':
            compress = 1;//-c，压缩文件
            break;
        case 'd':
            compress = 0;//-d，解压缩文件
            break;
        case 'h':
            usage(stdout);//-h，help
            return 0;
        case 'v':
            version(stdout);//-v，输出版本信息
            return 0;
        case 'm':
            memory = 1;//-m，对内存操作
            break;
        case 't':
            file_out_table = optarg;//-t，输出统计数据的表格          
            break;
        default:
            usage(stderr);//其他情况，将使用方法送到标准错误文件
            return 1;
        }
    }

    /* If an input file is given then open it.若为输入文件名，则打开*/
    if(file_in)
    {
        in = fopen(file_in, "rb");
        if(!in)
        {
            fprintf(stderr,
                    "Can't open input file '%s': %s\n",
                    file_in, strerror(errno));//返回错误的字符串
            return 1;
        }
    }

    /* If an output file is given then create it.若为输出文件名，则创建*/
    if(file_out)
    {
        out = fopen(file_out, "wb");
        if(!out)
        {
            fprintf(stderr,
                    "Can't open output file '%s': %s\n",
                    file_out, strerror(errno));//将错误的标号转换为表示错误的字符串
            return 1;
        }
    }

    if(memory)//若memory为1，则对内存操作
    {
        return compress ?
            memory_encode_file(in, out) : memory_decode_file(in, out);
        //若compress为1，内存编码；为0，内存解码
    }

    return compress ?
        huffman_encode_file(in, out) : huffman_decode_file(in, out);
    //memory为0，对文件操作。compress为1，文件编码；为0，文件解码
}

4.huffman.c

首先建立Huffman二叉树结构。
Huffman节点：

typedef struct huffman_node_tag
{
    unsigned char isLeaf;//是否为树叶节点
    unsigned long count;//相同信源符号出现的个数
    struct huffman_node_tag *parent;//父节点指针

    union
    {
        struct
        {
            struct huffman_node_tag *zero, *one;
        };
        unsigned char symbol;
    };//如果不是树叶，则该项表示该节点左右孩子的指针；否则为信源符号
} huffman_node;

Huffman码字节点：

typedef struct huffman_code_tag
{
    /* 码字的长度，以 位 为单位 */
    unsigned long numbits;

    /* 码字的第 1 位存于 bits[0]的第 1 位,
       码字的第 2 位存于 bits[0]的第的第 2 位,
       码字的第 8 位存于 bits[0]的第的第 8 位,
       码字的第 9 位存于 bits[1]的第的第 1 位  */
    unsigned char *bits;
} huffman_code;

Huffman统计表格，用来输出实验结果：

typedef struct huffman_statistics_result
    {
        float freq[256];
        unsigned long numbits[256];
        unsigned char bits[256][100];
    }huffman_stat;

Huffman的【文件编码】流程为：读取源文件->第一次扫描，统计各个信源符号出现的概率->建立Huffman树->将码表和其他必要信息写入输出文件->第二次扫描，对源文件编码并输出。

/*创建两个由256个元素组成的指针数组，分别保存信源符号的频率和码字*/
#define MAX_SYMBOLS 256
typedef huffman_node* SymbolFrequencies[MAX_SYMBOLS];
typedef huffman_code* SymbolEncoder[MAX_SYMBOLS];

对文件进行编码的主体函数：

int
huffman_encode_file(FILE *in, FILE *out,FILE *out_Table)
{
    SymbolFrequencies sf;//sf是存放符号的频率
    SymbolEncoder *se;//se是指向码字数组的指针
    huffman_node *root = NULL;//根节点的指针为NULL
    int rc;//返回值
    unsigned int symbol_count;//存放信源符号出现的频率
    huffman_stat hs;

    /* Get the frequency of each symbol in the input file. */
    symbol_count = get_symbol_frequencies(&sf, in);//第一次扫描后，得到每个符号出现的频率，赋值给symbol_count
    huffST_getSymFrequencies(&sf,&hs,symbol_count);

    /* Build an optimal table from the symbolCount. */
    se = calculate_huffman_codes(&sf);//所有码字节点指针存放在se中 
    root = sf[0];//将sf[0]设为根节点

    huffST_getcodeword(se, &hs);//获得码字
    output_huffman_statistics(&hs,out_Table);//建立码表

    /* Scan the file again and, using the table
       previously built, encode it into the output file. */
    rewind(in);//重新返回文件起始位置，准备进行第二次扫描
    rc = write_code_table(out, se, symbol_count);//将码表写进输入文件中
    if(rc == 0)//返回值为0，则成功写进码表
        rc = do_file_encode(in, out, se);//第二次扫描后，根据码表进行编码

    /* Free the Huffman tree. */
    free_huffman_tree(root);//释放huffman树
    free_encoder(se);//释放码字数组
    return rc;
}

对主体函数涉及到的变量依次进行结构体声明：

①统计各符号的频率

static unsigned int
get_symbol_frequencies(SymbolFrequencies *pSF, FILE *in)//统计频率
{
    int c;
    unsigned int total_count = 0;//扫描的总数初始值为0

    /* Set all frequencies to 0. */
    init_frequencies(pSF);//*pSF数组中所有元素初始化为0 

    /* Count the frequency of each symbol in the input file. */
    while((c = fgetc(in)) != EOF)//扫描输入文件，如果符号存在
    {
        unsigned char uc = c;
        if(!(*pSF)[uc])
            (*pSF)[uc] = new_leaf_node(uc);//如果是新符号，建立新的树叶节点
        ++(*pSF)[uc]->count;//树叶节点次数+1
        ++total_count;//总数+1
    }

    return total_count;
}

在上述结构体中需要对[树叶节点]进行声明：

static huffman_node*
new_leaf_node(unsigned char symbol)//新建树叶节点
{
    huffman_node *p = (huffman_node*)malloc(sizeof(huffman_node));
    p->isLeaf = 1;//将isLeaf设为1，表示树叶
    p->symbol = symbol;//存放信源符号
    p->count = 0;//初始值为0
    p->parent = 0;//父节点未知，设为0
    return p;
}

②按频率从小到大顺序排序，建立Huffman树

static SymbolEncoder*
calculate_huffman_codes(SymbolFrequencies * pSF)
{
    unsigned int i = 0;
    unsigned int n = 0;
    huffman_node *m1 = NULL, *m2 = NULL;//m1左子节点指针，m2右子节点指针
    SymbolEncoder *pSE = NULL;//*pSE表示存放码字节点的指针，初始值为NULL

#if 0
    printf("BEFORE SORT\n");
    print_freqs(pSF);//输出未排序前统计的频率，if-endif调试时使用，可以输出中间结果
#endif

    /* Sort the symbol frequency array by ascending frequency. */
    qsort((*pSF), MAX_SYMBOLS, sizeof((*pSF)[0]), SFComp);//qsort是排序函数，SFComp为升序排列

#if 0   
    printf("AFTER SORT\n");
    print_freqs(pSF);//输出排序后统计的频率 
#endif

    /* Get the number of symbols. */
    for(n = 0; n < MAX_SYMBOLS && (*pSF)[n]; ++n)
        ;//统计信源符号数

    /* Construct a Huffman tree. */
    for(i = 0; i < n - 1; ++i)
    {
        /* Set m1 and m2 to the two subsets of least probability. */
        m1 = (*pSF)[0];
        m2 = (*pSF)[1];//将m1，m2设为频率最小的两个元素

        /* Replace m1 and m2 with a set {m1, m2} whose probability
         * is the sum of that of m1 and m2. */
        (*pSF)[0] = m1->parent = m2->parent =
            new_nonleaf_node(m1->count + m2->count, m1, m2);
        (*pSF)[1] = NULL;
        //合并m1和m2，频率之和作为父节点的频率，(*pSF)[0]指向合并后的节点，(*pSF)[1]置NULL

        /* Put newSet into the correct count position in pSF. */
        qsort((*pSF), n, sizeof((*pSF)[0]), SFComp);//对n-1个数据进行重新排序
    }

    /* Build the SymbolEncoder array from the tree. */
    pSE = (SymbolEncoder*)malloc(sizeof(SymbolEncoder));//为码字节点指针数组开辟内存空间
    memset(pSE, 0, sizeof(SymbolEncoder));//数组初始化
    build_symbol_encoder((*pSF)[0], pSE);//建立所有码字节点
    return pSE;
}

在上述结构体中，需要对以下变量或函数声明：

a.非树叶节点，即中间节点

static huffman_node*
new_nonleaf_node(unsigned long count, huffman_node *zero, huffman_node *one)
{
    huffman_node *p = (huffman_node*)malloc(sizeof(huffman_node));
    p->isLeaf = 0;//节点不是树叶，值设为0
    p->count = count;
    p->zero = zero;//左子节点为0
    p->one = one;//右子节点为1
    p->parent = 0;

    return p;
}

b.用SFComp()函数进行升序排列

static int
SFComp(const void *p1, const void *p2)
{
    const huffman_node *hn1 = *(const huffman_node**)p1;
    const huffman_node *hn2 = *(const huffman_node**)p2;////把两个指针定义为树节点

    /* Sort all NULLs to the end. */
    if(hn1 == NULL && hn2 == NULL)
        return 0;//如果节点都为NULL，返回0
    if(hn1 == NULL)
        return 1;//如果第一个为NULL，说明第二个>第一个，满足要求，返回1
    if(hn2 == NULL)
        return -1;//如果第二个为NULL，说明第一个>第二个，返回-1

    if(hn1->count > hn2->count)
        return 1;//两个节点的数值进行比较
    else if(hn1->count < hn2->count)
        return -1;

    return 0;
}

③递归遍历Huffman树，计算码字

static void
build_symbol_encoder(huffman_node *subtree, SymbolEncoder *pSF)
{
    if(subtree == NULL)
        return;//如果第一次的树为NULL，则返回

    if(subtree->isLeaf)
        (*pSF)[subtree->symbol] = new_code(subtree);//如果是树叶，则产生码字
    else
    {
        build_symbol_encoder(subtree->zero, pSF);
        build_symbol_encoder(subtree->one, pSF);//如果不是树叶，递归，进行中序遍历
    }
}

上述结构体使用new_code产生码字，声明如下：

static huffman_code*
new_code(const huffman_node* leaf)
{
    /* Build the huffman code by walking up to
     * the root node and then reversing the bits,
     * since the Huffman code is calculated by
     * walking down the tree. */
    unsigned long numbits = 0;//初始化码长
    unsigned char* bits = NULL;//初始化码字首地址
    huffman_code *p;//定义码字节点指针

    while(leaf && leaf->parent)//leaf！=0，当前字符存在，可以编码；leaf->parent !=0，当前字符的编码仍未完成，即未完成由叶至根的该字符的编码过程
    {
        huffman_node *parent = leaf->parent;//当前的父节点
        unsigned char cur_bit = (unsigned char)(numbits % 8);//所编位在当前byte中的位置
        unsigned long cur_byte = numbits / 8;//当前是第几个byte

        /* If we need another byte to hold the code,
           then allocate it. */
        if(cur_bit == 0)//重新分配字节
        {
            size_t newSize = cur_byte + 1;//当前字节数+1，为新字节
            bits = (char*)realloc(bits, newSize);//realloc与malloc不同，它在保持原有数据不变的情况下重新分配新的内存空间，原有数据存在新空间中的前面
            bits[newSize - 1] = 0; //初始化新分配的8bit
        }

        /* If a one must be added then or it in. If a zero
         * must be added then do nothing, since the byte
         * was initialized to zero. */
        if(leaf == parent->one)//如果是右子节点，需要进行移位运算；左子节点不需要，因为初始化已为0
            bits[cur_byte] |= 1 << cur_bit;//左移一位至当前byte的当前位

        ++numbits;
        leaf = parent;//将父节点赋值给新的叶节点
    }

    if(bits)
        reverse_bits(bits, numbits);//bits包含1，则整个码字逆序

    p = (huffman_code*)malloc(sizeof(huffman_code));
    p->numbits = numbits;//编码所需位数
    p->bits = bits;//整数个字节，与numbits配合才能得到真正码字
    return p;//返回码字节点指针
}

new_code中又使用了reverse_bits()，具体如下：

static void
reverse_bits(unsigned char* bits, unsigned long numbits)
{
    unsigned long numbytes = numbytes_from_numbits(numbits);
    unsigned char *tmp =
        (unsigned char*)alloca(numbytes);//alloca是在栈上开辟空间
    unsigned long curbit;//当前比特数
    long curbyte = 0;

    memset(tmp, 0, numbytes);//tmp数组初始化

    for(curbit = 0; curbit < numbits; ++curbit)
    {
        unsigned int bitpos = curbit % 8;//左移位数

        if(curbit > 0 && curbit % 8 == 0)
            ++curbyte;//如果当前byte逆序完毕，则至下一byte

        tmp[curbyte] |= (get_bit(bits, numbits - curbit - 1) << bitpos);//如果get_bit()第二个参数是0，则是bit[0]最右位；为numbits-curbit-1时，则为bit[numbytes-1]的最左位
    }

    memcpy(bits, tmp, numbytes);//将tmp数据赋给bits
}

reverse_bits()中使用了numbytes_from_numbits()，具体如下：

static unsigned long
numbytes_from_numbits(unsigned long numbits)
{
    return numbits / 8 + (numbits % 8 ? 1 : 0);//numbits不足8位，需要补齐，计算所需字节数
}

new_code中还使用了get_bit()，具体如下：

static unsigned char
get_bit(unsigned char* bits, unsigned long i)
{
    return (bits[i / 8] >> i % 8) & 1;//返回bit[0]位置时的值
}

④将码表和其他必要信息写入输出文件

static int
write_code_table(FILE* out, SymbolEncoder *se, unsigned int symbol_count)
{
    unsigned long i, count = 0;

    /* Determine the number of entries in se. */
    for(i = 0; i < MAX_SYMBOLS; ++i)
    {
        if((*se)[i])
            ++count;//计算字符的种类
    }

    /* Write the number of entries in network byte order. */
    i = htonl(count);
    if(fwrite(&i, sizeof(i), 1, out) != 1)
        return 1;//将字符种类数写进输出文件

    /* Write the number of bytes that will be encoded. */
    symbol_count = htonl(symbol_count);
    if(fwrite(&symbol_count, sizeof(symbol_count), 1, out) != 1)
        return 1;//将输入文件字符数写进输出文件

    /* Write the entries. */
    for(i = 0; i < MAX_SYMBOLS; ++i)//将Huffman码表写入文件
    {
        huffman_code *p = (*se)[i];
        if(p)
        {
            unsigned int numbytes;
            /* Write the 1 byte symbol. */
            fputc((unsigned char)i, out);//写入符号
            /* Write the 1 byte code bit length. */
            fputc(p->numbits, out);//写入符号的长度
            /* Write the code bytes. */
            numbytes = numbytes_from_numbits(p->numbits);//写入码字
            if(fwrite(p->bits, 1, numbytes, out) != numbytes)
                return 1;
        }
    }

    return 0;
}

⑤第二次扫描文件，对文件查表进行Huffman编码，并写入文件

static int
do_file_encode(FILE* in, FILE* out, SymbolEncoder *se)
{
    unsigned char curbyte = 0;
    unsigned char curbit = 0;
    int c;

    while((c = fgetc(in)) != EOF)//遍历每个字节
    {
        unsigned char uc = (unsigned char)c;
        huffman_code *code = (*se)[uc];//查表，找到当前字符uc对应的code
        unsigned long i;

        for(i = 0; i < code->numbits; ++i)
        {
            /* Add the current bit to curbyte. */
            curbyte |= get_bit(code->bits, i) << curbit;//将当前的bit放进编码字节对应的位置，变成二进制

            /* If this byte is filled up then write it
             * out and reset the curbit and curbyte. */
            if(++curbit == 8)
            {
                fputc(curbyte, out);
                curbyte = 0;
                curbit = 0;
            }//如果字节被填满，则输出。curbit和curbyte都设为0
        }
    }

    /*
     * If there is data in curbyte that has not been
     * output yet, which means that the last encoded
     * character did not fall on a byte boundary,
     * then output it.
     */
    if(curbit > 0)
        fputc(curbyte, out);//如果最后一个curbyte没有写满，则不会继续写入文件。当curbit>0时，将最后一个curbyte写入文件

    return 0;
}

⑥输出结果，需要实现三个函数

/********统计各符号出现的概率*********/
int huffST_getSymFrequencies(SymbolFrequencies *SF, huffman_stat *st,int total_count)
{
    int i,count =0;
    for(i = 0; i < MAX_SYMBOLS; ++i)
    {   
        if((*SF)[i])
        {
            st->freq[i]=(float)(*SF)[i]->count/total_count;
            count+=(*SF)[i]->count;//对符号进行遍历，概率->相同符号出现的次数/总数
        }
        else 
        {
            st->freq[i]= 0;
        }
    }
    if(count==total_count)
        return 1;
    else
        return 0;
}
/***********************************/

/******统计各符号对应的码长和码字*******/
int huffST_getcodeword(SymbolEncoder *se, huffman_stat *st)
{
    unsigned long i,j;

    for(i = 0; i < MAX_SYMBOLS; ++i)
    {
        huffman_code *p = (*se)[i];
        if(p)
        {
            unsigned int numbytes;
            st->numbits[i] = p->numbits;
            numbytes = numbytes_from_numbits(p->numbits);
            //这里用到了numbytes_from_numbits，补足8位字节数
            for (j=0;jbits[i][j] = p->bits[j];
        }
        else
            st->numbits[i] =0;
    }

    return 0;
}
/********************************/

/*******输出所有的统计信息********/
int output_huffman_statistics(huffman_stat *st,FILE *out_Table)
{
    int i,j;
    unsigned char c;
    fprintf(out_Table,"symbol\t   freq\t   codelength\t   code\n");
    for(i = 0; i < MAX_SYMBOLS; ++i)
    {   
        fprintf(out_Table,"%d\t   ",i);//符号
        fprintf(out_Table,"%f\t   ",st->freq[i]);//频率
        fprintf(out_Table,"%d\t    ",st->numbits[i]);//码长
        if(st->numbits[i])
        {
            for(j = 0; j < st->numbits[i]; ++j)
            {
                c =get_bit(st->bits[i], j);
                fprintf(out_Table,"%d",c);//码字
            }
        }
        fprintf(out_Table,"\n");
    }
}
/*********************************/

三、 实验结果

以表格形式表示的实验结果(参考把文本导入表格的步骤)如下：

文件类型	平均码长	信源熵	原大小(kB)	压缩后的大小(kB)	压缩比
1.pdf	8.4689	8.4956	207	206	1.00485
2.ppt	1.055331	0.940841	185	131	1.41221
3.opt	0.76733	0.443697	61	22	2.77272
4.cif	0.000312	0.0003	3564	2919	1.22096
5.dat	0.942148	0.805334	1	1	1
6.qws	0.168916	0.167256	1	1	1
7.wav	1.939	1.927	108	81	1.33333
8.docx	0.31908	0.305203	40	40	1
9.ldf	0.082669	0.081982	19	14	1.35714
10.bin	1.117309	0.534228	8	2	4

各样本文件的概率分布图如下：






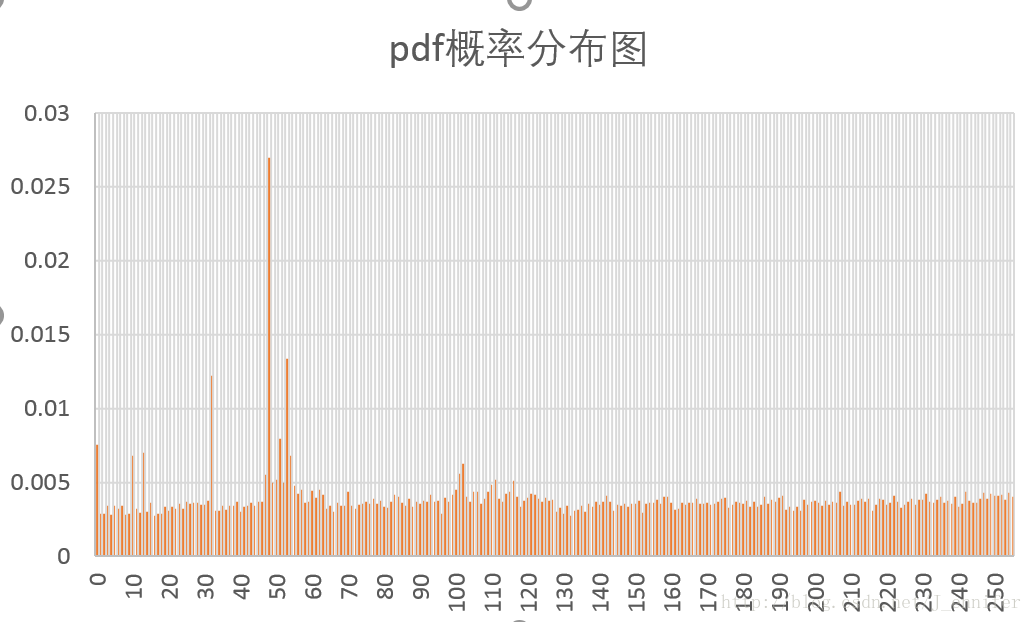
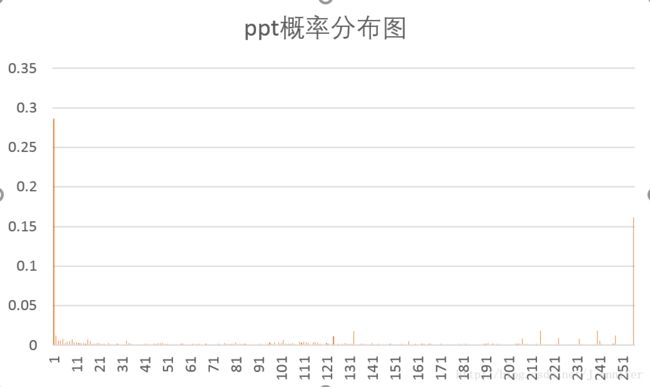
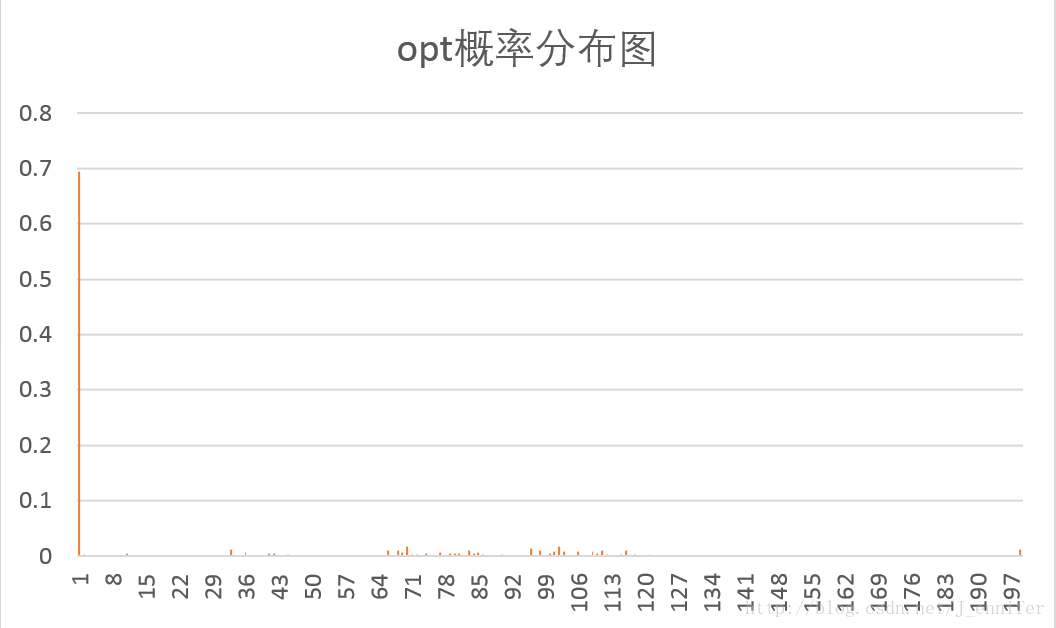
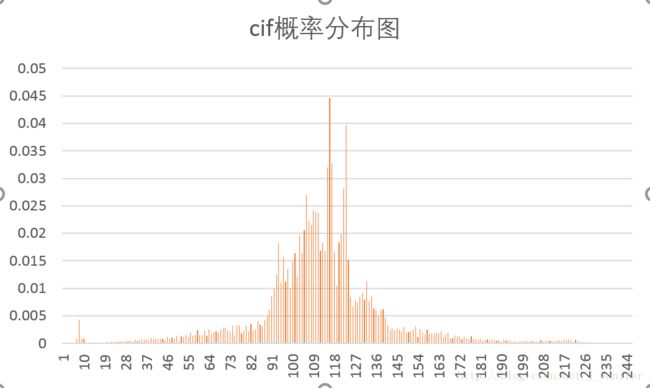
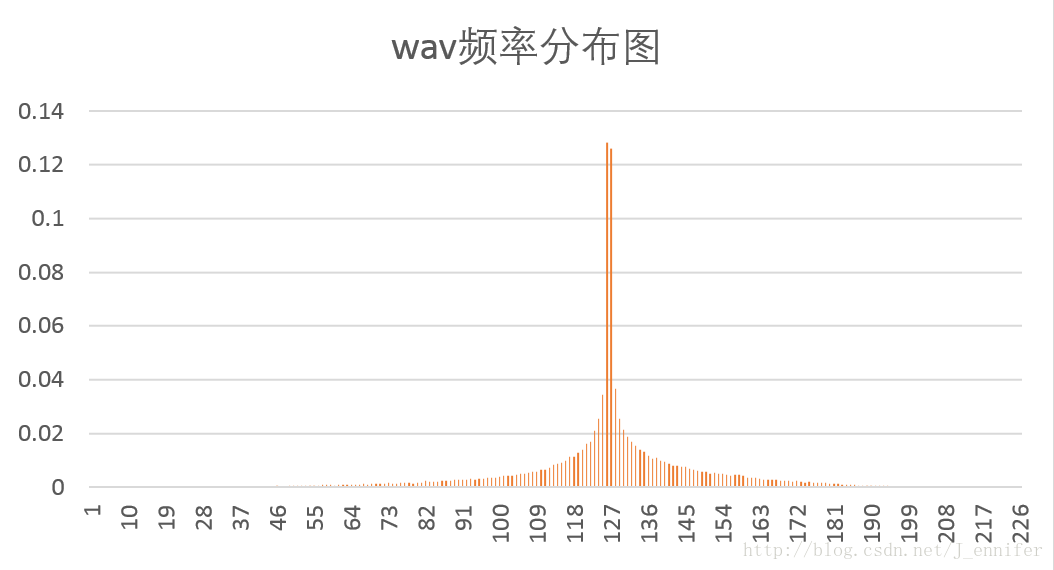
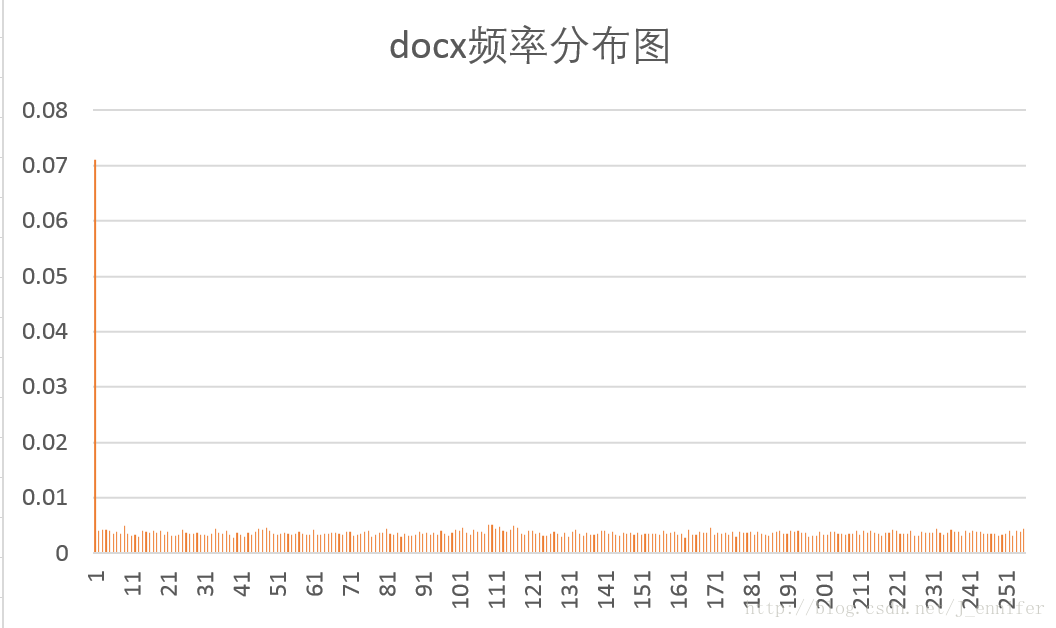
由于我选的测试文件大都“不正常”，输出的结果不理想。故只选了几张看似比较正常的图像输出。
从图像结果可以看出，Huffman编码对概率分布不均匀的文件压缩效果好，而对信源符号概率接近相等的文件基本没有压缩。同时也验证了香农第一定理，即无失真信源编码定理，对于二进制码信源符号，平均码长的下界为信源熵。

四、错误分析

①刚开始编译程序，发现出错：

这是因为没有把lib文件与主程序链接。将两个工程分别写好后，需要实现静态链接库Huff_code和主工程Huff_run的连接，还有命令行参数的设置。具体步骤是：
a.编译Huff_code，在Debug文件夹中会生成Huff_code.lib。
b.将Huff_code.lib复制到主工程Huff_run中，操作为：
项目->属性->配置属性->链接器->常规->附加库目录，添加Huff_code.lib的路径；
项目->属性->配置属性->链接器->输入->附加依赖项，添加Huff_code.lib。
c.将huffman.h添加到Huff_run的外部依赖项中：
项目->属性->配置属性->VC++目录->包含目录：添加huffman.h的路径。
d.编译Huff_run，进行命令行参数设置：
项目->属性->配置属性->调试->设置命令参数和工作目录。
命令行参数示例：-i 1.pdf -o 1.huf -c -t 1.txt
②Huff_run编译时出现无法解析的外部符号：

改正：在huffcode.c文件的#include指令的下方添加一条指令->#pragma comment(lib,"ws2_32.lib")
③调试时出现错误：”cannot find or open pdb file.”无法解决，导致实验结果不能正确出现。本文实验结果是借用别人的程序实现的。
④把文本文档导入表格的步骤：
单击第一个单元格->数据选项卡->自文本->导入文本文件->依次选择“分隔符号”,“Tab键”,“常规”->确定
对平均码长的计算：平均码长=（概率*长度）求和
对信源熵的计算：信源熵=（-概率*log(概率,2)）求和
压缩比的计算：原文件大小/压缩后的文件大小