奇虎360 2017春招笔试编程题详解
目录
- 跑步
- 题目描述
- 题目解析
- Java解答
- 剪气球串
- 题目描述
- 题目解析
- Java解答
- 分金子
- 题目描述
- 题目解析
- Java解答
跑步
题目描述:
小明同学喜欢体育锻炼,他常常去操场上跑步。跑道是一个圆形,在本题中,我们认为跑道是一个半径为R的圆形,设圆心的坐标为原点(0,0)。
小明跑步的起点坐标为(R,0),他沿着圆形跑道跑步,而且一直沿着一个方向跑步。回到家后,他查看了自己的计步器,计步器显示他跑步的总路程为L。
小明想知道自己结束跑步时的坐标,但是他忘记自己是沿着顺时针方向还是逆时针方向跑的了。他想知道在这两种情况下的答案分别是多少。
输入:
输入两个整数L,R (1<=L,R<=100)。
输出:
输出两行,每行两个数,用空格隔开。
第一行的两个数为顺时针情况下结束位置的坐标,第二行是逆时针情况下结束位置的坐标。
所有数据小数点后四舍五入保留3位。
样例输入:1 2
样例输出:1.755 -0.959
1.755 0.959
题目解析:
这题没啥好说的,直接数学方法求解,看代码吧。
Java解答:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Main p = new Main();
p.solve();
}
private void solve() {
Scanner in = new Scanner(System.in);
while(in.hasNext()){
float l = in.nextInt();
float r = in.nextInt();
// 这里分别求出cos(θ)和sin(θ)
float x=(float)(r*Math.cos(l/r));
float y=(float)(r*Math.sin(l/r));
System.out.printf("%.3f %.3f\n",x,-y);
System.out.printf("%.3f %.3f\n",x,y);
}
in.close();
}
}
剪气球串
题目描述:
小明买了一些彩色的气球用绳子串在一条线上,想要装饰房间,每个气球都染上了一种颜色,每个气球的形状都是各不相同的。
我们用1到9一共9个数字表示不同的颜色,如12345则表示一串5个颜色各不相同的气球串。但小明希望得到不出现重复颜色的气球串,那么现在小明需要将这个气球串剪成多个较短的气球串,小明一共有多少种剪法?如原气球串12345的一种是剪法是剪成12和345两个气球串。
注意每种剪法需满足最后的子串中气球颜色各不相同(如果满足该条件,允许不剪,即保留原串)。两种剪法不同当且仅当存在一个位置,在一种剪法里剪开了,而在另一种中没剪开。详见样例分析。
输入:
第一行输入一个正整数n(1≤n≤100000),表示气球的数量。
第二行输入n个整数a1,a2,a3...an,ai表示该气球串上第i个气球的颜色。对于任意i,有1≤ai≤9。
输出:
输出一行,第一行输出一个整数,表示满足要求的剪法,输出最终结果除以1000000007后的余数。
样例输入:
3
1 2 3
样例输出:
4
题目解析:
题意:
本题题意可以抽象成一个数学的表述,即一个长度为n的数组,每一个数的范围是1到9,现在我们需要将这个数组分成多个连续子数组,保证每个子数组内数字均不相同,问一共有多少种满足要求的分法。
例:输入3 1 2 3。输出4。
我们有以下4种剪法,* 表示在这个位置剪,没有* 则表示不剪:
1* 2* 3
1* 2 3
1 2* 3
1 2 3
解法:
这题需要用到动态规划进行求解,我们不妨记一个数组dp[i],表示这个数组前i个数组成的数组可以有多少种分法,数组初始全为0,特别的dp[0]初始为1。
那么在计算dp[i+1]时,我们需要考虑第i+1个数可以和前面哪些数分到一起组成连续的子数组。 比如:
第i+1个数可以和第i个数组成一组,但不能和第i-1个数分到一组,那么dp[i+1]=dp[i]+dp[i-1];
第i+1个数可以单独组成一组,有:dp[i+1]+=dp[i];
第i+1个数和第i个数组成一组,有:dp[i+1]+=dp[i-1];
由于每个数的范围是1到9,所有最多只需要按照这种方法枚举第i+1个数前面的9个数即可停止。算法复杂度O(n*10)。详见代码。
Java解答:
import java.util.HashSet;
import java.util.Scanner;
// 剪气球串问题
public class Main {
public static void main(String[] args) {
Main p = new Main();
p.input();
}
@SuppressWarnings("resource")
private void input() {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] array = new int [n];
int index = 0;
while (index set = new HashSet<>();
int j = i-1;
while (j>=0 && !set.contains(array[j])){
set.add(array[j]);
dp[i] += dp[j];
dp[i] = (int) (dp[i] % (Math.pow(10,9)+7));
j--;
}
}
System.out.println(dp[n]);
return ;
}
}
分金子
题目描述:
A、B两伙马贼意外地在一片沙漠中发现了一处金矿,双方都想独占金矿,但各自的实力都不足以吞下对方,经过谈判后,双方同意用一个公平的方式来处理这片金矿。
处理的规则如下:他们把整个金矿分成n段,由A、B开始轮流从最左端或最右端占据一段,直到分完为止。
马贼A想提前知道他们能分到多少金子,因此请你帮忙计算他们最后各自拥有多少金子?(两伙马贼均会采取对己方有利的策略)
输入:
测试数据包含多组输入数据。
输入数据的第一行为一个正整数T(T<=20),表示测试数据的组数。
然后是T组测试数据,每组测试数据的第一行包含一个整数n;
下一行包含n个数(n <= 500 ),表示每段金矿的含金量,保证其数值大小不超过1000。
输出:
对于每一组测试数据,输出一行"Case #id: sc1 sc2",
表示第id组数据时马贼A分到金子数量为sc1,马贼B分到金子数量为sc2。
详见样例。
样例输入:
2
6
4 7 2 9 5 2
10
140 649 340 982 105 86 56 610 340 879
样例输出:
Case #1: 18 11
Case #2: 3206 981
题目解析
题意:
本题可以看成一个博弈问题,给出一个长度为n的序列:a1; a2; …… ; an,两个人轮流取出序列中的元素,他们每次只能取出当前序列最左边或者最右边的元素,直到把序列中所有的元素都取完,每个人都希望自己取出的元素总和最大,问两人取出的总和各为多少?
举几个简单的例子:
考虑如下序列:1; 100
先手一定取出100,后手只能取1。
再看下面一个序列:10; 1000; 2; 1
先手第一步可以取出10或者1,但是如果先手取出10,那么后手下一轮会取走1000,先手得不偿失,所以先手第一步取走1。
此时序列变成:10; 1000; 2 这时候后手不论怎么取,先手在下一轮一定会取走1000。所以最后先手取出的总和为1001,后手为12。
解法:
考虑先手和后手在序列a(1); a(2);……; a(n)上博弈:
① 如果先手取走了a1,那么问题转化成了两个人在a(2); a(3);……; a(n)上的博弈。
② 如果先手取走an,就变成了在a(1); a(2);……; a(n-1)上的博弈。
于是,有了如下解题思路:
可以定义f(L; R)为两个人在序列a(L); a(L+1);……; a(R)上博弈时,先手最多能拿到多少价值,注意到后手拿到的价值一定为
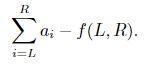
① 很容易找到f(L; R)的初始情况,即博弈序列长度为1的时候:先手直接拿走唯一元素:
![]()
② 现在考虑 L < R,若先手拿a(L),那么问题变成了两人在a(L+1); a(L+2); ……; a(R)上的博弈,而且后手在这个新的博弈问题上可以获得f(L+1; R)的价值,所以先手能获得的总价值为:
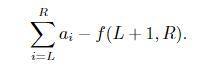 同理可以得到先手拿a(R)的情况。
同理可以得到先手拿a(R)的情况。
Java解答
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Main p = new Main();
p.solve();
}
private void solve() {
Scanner in = new Scanner(System.in);
int num = in.nextInt();
for (int i=1; i<=num; i++){
int n = in.nextInt();
// 记录n份金子
int[] array = new int[n+1];
// 前i份金子的数量之和
int[] sum = new int[n+1];
array[0] = 0;
sum[0] = 0;
for (int j=1; j<=n; j++) {
array[j] = in.nextInt();
sum[j] = sum[j-1] + array[j];
}
// 动态规划数组
int[][] f = new int[n+1][n+1];
for (int j=1; j<=n; j++)
// 记录对角线元素
f[j][j] = array[j];
int k=1;
while (k <= n-1){
// 从对角线元素开始计算,向右上挪动直至计算到f[1][n]
for (int j=1; j+k<=n; j++){
f[j][j+k] = sum[j+k] - sum[j-1] - Math.min(f[j][j+k-1], f[j+1][j+k]);
}
k++;
}
System.out.println("Case #"+i+": "+f[1][n]+" "+(sum[n]-f[1][n]));
}
in.close();
}
}
注:本文中的题目及部分解析来自赛码网(http://www.acmcoder.com/index)。