线性代数(21)——特征值和特征向量(下)

numpy中求取特征值和特征向量

特征值和特征向量的求取不进行编程实现，因为整个求取过程中最重要的是求解 $det(A-\lambda I)=0$ 对应的$n$次方程，其中$n$是矩阵$A$的阶数。

import numpy as np
from np.linalg import eig	# eigen缩写


if __name__ == "__main__":
	A1 = np.array([[4, -2], [1, 1]])
	# eig方法两个返回值，分别是特征值和特征向量
	eigen_values, eigen_vectors = eig(A1)
	print(eigen_values)	# [3.0, 2.0]
	print(eigen_vectors)	# [[0.8944..., 0.7071...], [0.4472..., 0.7071...]]

	A2 = np.array([[0, 1], [1, 0]])
    e_values, e_vectors = eig(A2)
    print(e_values)    # [1.0, -1.0]    
    print(e_vectors)   # [[0.7071, -0.7071], [0.7071, 0.7071]]

	# 复数特征值
	A3 = np.array([[0, -1], [1, 0]])
    e_values, e_vectors = eig(A3)
    print(e_values)    # [0.0+1.0j, 0.0-1.0j]
    print(e_vectors)   # [[0.7071 + 0j, 0.7071 - 0j], [0 - 0.7071j, 0 + 0.7071j]]

	# 多重特征值
	A4 = np.array([[1, 0], [0, 1]])
    e_values, e_vectors = eig(A4)
    print(e_values)    # [1.0, 1.0]
    print(e_vectors)   # [[1, 0], [0, 1]]

	A5 = np.array([[3, 1], [0, 3]])
    e_values, e_vectors = eig(A5)
    print(e_values)    # [3.0, 3.0]
    # [1, 0]和[-1, 0]实际上是线性相关（共线）的，这种结果产生是因为numpy本身内部的算法
    print(e_vectors)   # [[1, -1], [0, 0]]    

矩阵的相似型(相似矩阵)

这一节是在为之后理解特征值和特征向量的具体用途进行铺垫。同时也是理解特征值和特征向量中“特征”一词在矩阵中具体的指代。

定义

如果矩阵$A$和$B$满足，$A=P^{-1}BP$ 则称矩阵$A$和$B$相似。

理解这一概念可以类比相似三角形，回顾相似三角形，指的是三个内角相同，而三边的长度没有具体要求的两个三角形（即形状一样，大小不一样）。两个矩阵的相似和相似三角形一样，都是从不同的视角观察相同的内容，$A=P^{-1}BP$这个关系式中，$P$可以视为一个坐标系，则$A$变换是在$P$坐标系下观察的$B$变换。对这句话进行讲解，

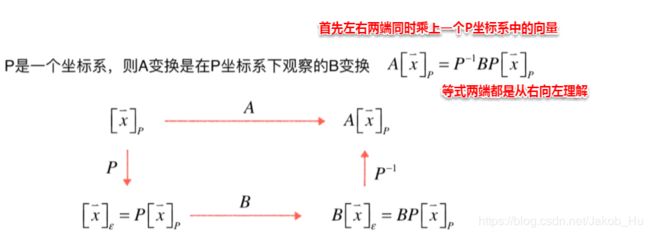
上面的这张图可以分解成两部分，分别是最上面的边和下面三条边构成的循环，

1. 最上面的边
   最上面的边表示的是$P$坐标系中的向量$x$经过矩阵$A$变换得到的结果，该结果依旧是在$P$坐标系中。
2. 下方循环
   首先将向量$x$通过$P$坐标系的坐标转换矩阵$P$得到标准坐标系下对应的向量。
   在标准坐标系下通过矩阵$B$变换得到一个结果，该结果存在于标准坐标系下。
   将上述标准坐标系中的向量通过$P^{-1}$进行转换，得到其在$P$坐标系中的向量。

依据 $A=P^{-1}BP$这个关系式，可知两个部分最终的结果是相同的，也可以理解为$A$和$B$这两个变换本质上是一个变换，只是两个变换过程所在的坐标系是不同的（$A$在$P$坐标系下的变换与$B$在标准坐标系下的变换是一样的）。这也是相似矩阵的几何含义。

注意P和P^(-1)的顺序

之前的公式 $A=P^{-1}BP$的另一个形式是 $B=PA{P}^{-1}$。通过前面的式子得到后面的这个式子是很简单的。需要注意的地方在于，

• 如果$P$在前，$P^{-1}$在后，则$P$和$P^{-1}$之间夹着的变换是在$P$坐标系下进行的。
• 如果$P^{-1}$在前，$P$在后，则$P$和$P^{-1}$之外的变换是在$P$坐标系下进行的。

这个规律是不需要背的，可以很容易的通过上面的两个式子理解（从右向左理解），

1. $A=P^{-1}BP$
   $P$在最后，说明第一步的转换将$P$坐标系转换为标准坐标系，否则$P$这一步没有几何意义，之后的$B$转换是在标准坐标系中发生的。
2. $B=PA{P}^{-1}$
   $P^{-1}$在最后，说明第一步转换是在$P$坐标系中进行的，否则$P^{-1}$转换没有几何意义，之后的$A$转换是在$P$坐标系中发生的。

矩阵相似的本质

$A$和$B$是相似矩阵，则两个矩阵具有相同的特征方程，相应的它们的特征值是相同的。
这也就是特征值的本意，无论是在哪个坐标系下观察，$A$和$B$在不同的坐标系中的值并不相同，但是其特征方程和特征值是不变的。对上面的结论进行证明，

即证，当满足 $A=P^{-1}BP$的条件时，$A$和$B$的特征方程是一样的，意味着$A$和$B$的特征值是相同的。
特征方程和特征值相同表达的是当把矩阵看做是变换时，这个变换无论从哪个坐标系看，这些变换都有相同的特征，这些特征通过特征值表征出来。

矩阵对角化

概念

上面的结论证明出当矩阵看做是变换时，相似的矩阵在不同的坐标系下具有相同的特征。矩阵的对角化是尝试找出坐标系$P$使得某一个矩阵$A$所代表的变换能够在$P$坐标系中表示为一个对角矩阵$D$的变换，即 $A=PD{P}^{-1}$。对角矩阵的好处在于，它仅仅是对相同维度进行伸缩而不影响其他维度，这使得转换过程十分简单。

但是对角矩阵$D$是不一定存在的，因为矩阵$A$需要满足一定的条件，即如果$A$有$n$个线性无关的特征向量，则$A$和某个对角矩阵$D$相似，其中$n$是矩阵$A$的阶数。如果一个矩阵$A$代表的转换能够在$P$坐标系中表示为一个对角矩阵，则该对角矩阵的主对角线上的元素是矩阵$A$的$n$个特征值，而$P$这个坐标系的坐标转换矩阵的每一列就是各特征值对应的特征向量。

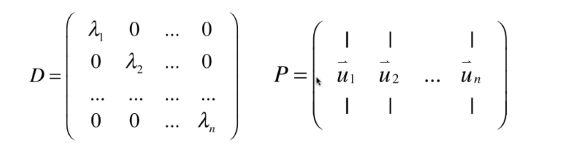
这也就是要求$A$矩阵满足上面的条件的原因，因为特征向量需要构成一组$n$维空间的基。

对上述结论进行证明，

回顾之前的结论，如果矩阵$A$含有两个不同的特征值，则他们对应的特征向量线性无关。对这一性质进行推广，当$A$有$n$个不同的特征值，$n$是矩阵$A$的阶数，则$A$可以被对角化。如果$A$没有$n$个不同的特征值，$A$不一定能被对角化，因为几何重数无法确定，只有在几何重数=代数重数，且对应的$n$个特征向量线性无关时，矩阵$A$才能够被对角化。

实现矩阵对角化

import numpy as np
from numpy import eig
from playLA.LinearSystem import rank
from playLA.Matrix import Matrix


def diagonalize(A):
    # 判断A是矩阵且是方阵
    assert A.ndim == 2
    assert A.shape[0] == A.shape[1]

    eigen_values, eigen_vectors = eig(A)
    
    # 矩阵对角化的P对应的就是特征向量构成的坐标转换矩阵
    P = eigen_vectos

    # 通过矩阵的秩判断P是否可逆，不满秩则不可逆
    if rank(Matrix(P.tolist())) != A.shape[0]:
        print("Matrix can not be diagonalized")
        return None, None, None

    D = np.diag(eigen_values)
    P_inv = np.inv(P)

    return P, D, P_inv


if __name__ == "__main__":
    # 能够对角化的情况
    A1 = np.array([[4, -2], [1, 1]])
    P1, D1, P_inv1 = diagonalize(A1)
    print(P1)        # [[0.8944, 0.7071]
                     #  [0.4472, 0.7071]]
    print(D1)        # [[3.0, 0.0]
                     #  [0.0, 2.0]]
    print(P_inv1)    # P的逆矩阵

    print(P1.dot(D1).dot(P_inv1))    # 与A相同

    # 无法对角化的情况
    A2 = np.array([[3, 1], [0, 3]])
    P2, D2, P_inv2 = diagonalize(A2)    # 输出相应提示
    

矩阵对角化应用

$A=PD{P}^{-1}$，$D$变换是$P$坐标系下观察到的$A$变换。
矩阵对角化便于进行矩阵的幂运算。
具体的幂运算推导过程如下，

对于一个对角矩阵而言，其幂运算结果也是一个对角矩阵，且这个结论能够推广到$n$次幂上，

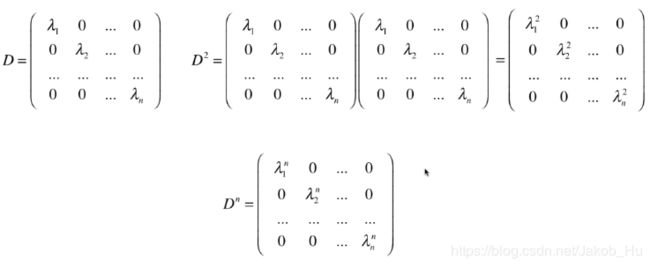
这使得计算不需要进行矩阵转换，计算消耗减少很多。

特征值反映的是系统各个部分分量在不同时刻空间的变换速率。而且对角化后的运算都会简便很多，日常采集的大部分数据也都是能够被对角化的。