c语言与matlab生成FFT结果对比
首先用C语言实现FFT的输出
一、程序内容
#include
#include
#include
#define N 1000
//定义复数类型
typedef struct
{
double real;
double img;
}complex;
void fft(); // 快速傅里叶变换
void initW(); // 初始化变换核
void change(); // 变址
void add(complex ,complex ,complex *); // 复数加法
void mul(complex ,complex ,complex *); // 复数乘法
void sub(complex ,complex ,complex *); // 复数减法
void divi(complex ,complex ,complex *); // 复数除法
void output(); // 输出快速傅里叶变换的结果
complex x[N], *W; // 输入序列,变换核
int size_x=0; // 输入序列的大小，在本程序中仅限2的次幂
double PI; // 圆周率
int main()
{
int i; // 输出结果
system(“cls”);
PI=atan(1)*4;
printf(“Please input the size of x:\n”); // 输入序列的大小
scanf("%d",&size_x);
printf(“Please input the data in x[N]:\n”); // 输入序列的实部和虚部
printf("Enter the sequence\n",i);
for (i = 0; i < size_x; i++)
{
scanf("%lf%lf",&x[i].real,&x[i].img);
}
initW(); //调用变换核
fft(); //调用快速傅里叶变换
printf("Output of FFT\n");
output(); //调用输出傅里叶变换结果函数
return 0;
}
/快速傅里叶变换/
void fft()
{
int i=0,j=0,k=0,l=0;
complex up,down,product;
change(); //调用变址函数
for(i=0;i< log(size_x)/log(2) ;i++) /一级蝶形运算 stage /
{
l=1<
{
for(k=0;k
{
mul(x[j+k+l],W[size_xk/2/l],&product);
add(x[j+k],product,&up);
sub(x[j+k],product,&down);
x[j+k]=up;
x[j+k+l]=down;
}
}
}
}
/初始化变换核，定义一个变换核，相当于旋转因子W/
void initW()
{
int i;
W=(complex )malloc(sizeof(complex) * size_x); //生成变换核
for(i=0;i
W[i].real=cos(2
W[i].img=-1sin(2PI/size_xi);
}
}
/变址计算，将x(n)码位倒置/
void change()
{
complex temp;
unsigned short i=0,j=0,k=0;
double t;
for(i=0;i
k=i;j=0;
t=(log(size_x)/log(2));
while( (t–)>0 ) //利用按位与以及循环实现码位颠倒
{
j=j<<1;
j|=(k & 1);
k=k>>1;
}
if(j>i) //将x(n)的码位互换
{
temp=x[i];
x[i]=x[j];
x[j]=temp;
}
}
}
/输出傅里叶变换的结果/
void output()
{
int i;
printf(“The result are as follows\n”);
for(i=0;i
printf("%.4f",x[i].real);
if(x[i].img>=0.0001)
printf("+%.4fj\n",x[i].img);
else if(fabs(x[i].img)<0.0001)
printf("\n");
else
printf("%.4fj\n",x[i].img);
}
}
void add(complex a,complex b,complex c) //复数加法的定义
{
c->real=a.real+b.real;
c->img=a.img+b.img;
}
void mul(complex a,complex b,complex c) //复数乘法的定义
{
c->real=a.realb.real - a.imgb.img;
c->img=a.realb.img + a.imgb.real;
}
void sub(complex a,complex b,complex c) //复数减法的定义
{
c->real=a.real-b.real;
c->img=a.img-b.img;
}
void divi(complex a,complex b,complex c)
{
c->real=(a.realb.real+a.imgb.img )/(b.realb.real+b.imgb.img);
c->img=(a.imgb.real-a.realb.img)/(b.realb.real+b.imgb.img);
}
运行后的结果:
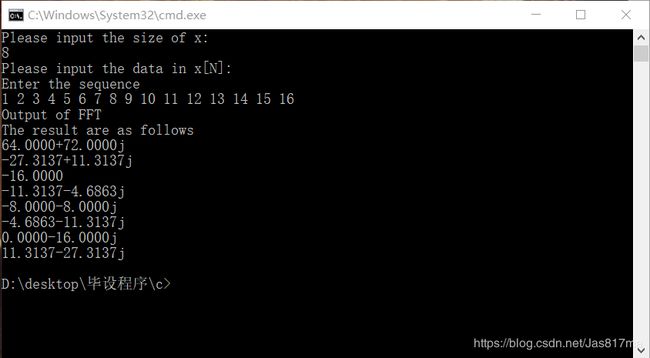二、FFT的MATLAB实现
1、有限长序列x（n）的DFT概念和公式：
2、FFT算法调用格式
Y=fft(x) 或 Y=fft (x，N)
其中N为采样点数，X为离散频域信号。
x的长度为2的整数次幂，N为2的整数次幂。若x的长度小于N，则在x末尾添加零，使得 x长度=n的长度；若超过N，则舍弃N以后的数据。
建议采用前一等式，并且保证x的个数为偶数
使用matlab来实现FFT计算：
%matlab实现FFT算法
N=input(‘Please input N=’);
x=input(‘Please input complex number sequence x[n]=’);
X=fft(x,N); n=0:N-1;
subplot(211);
stem(n,real(X));
title(‘Real Part’);
subplot(212);
stem(n,imag(X));
title(‘Image Part’);
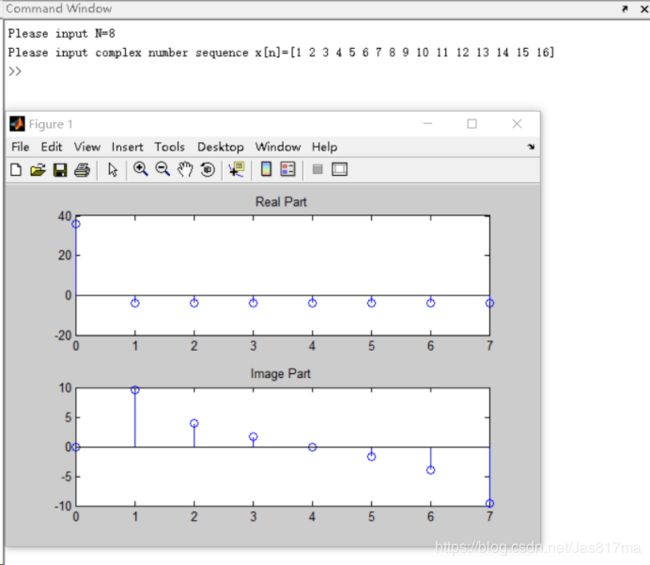通过对比C语言和Matlab实现的FFT结果发现计算结果存在差异。因为MATLAB中自带FFT函数，我们将其调用出来，先来观察其运算原理:
%FFT Discrete Fourier transform.
% FFT(X) is the discrete Fourier transform (DFT) of vector X. For
% matrices, the FFT operation is applied to each column. For N-D
% arrays, the FFT operation operates on the first non-singleton
% dimension.
%
% FFT(X,N) is the N-point FFT, padded with zeros if X has less
% than N points and truncated if it has more.
%
% FFT(X,[],DIM) or FFT(X,N,DIM) applies the FFT operation across the
% dimension DIM.
%
% For length N input vector x, the DFT is a length N vector X,
% with elements
% N
% X(k) = sum x(n)exp(-j2pi(k-1)(n-1)/N), 1 <= k <= N.
% n=1
% The inverse DFT (computed by IFFT) is given by
% N
% x(n) = (1/N) sum X(k)exp( j2pi*(k-1)*(n-1)/N), 1 <= n <= N.
% k=1
%
% See also FFT2, FFTN, FFTSHIFT, FFTW, IFFT, IFFT2, IFFTN.
% Copyright 1984-2005 The MathWorks, Inc.
% $Revision: 5.15.4.5 $ $Date: 2005/06/21 19:23:54 $
% Built-in function.
通过观察Matlab内部fft函数可知，对于X=fft(x,N)函数的使用，若x的长度小于N则补零，若超过N则舍弃N以后的数据。我们设定x长度为16，N为8，所以Matlab实际进行FFT的运算时只使用了序列前8个数值，后面的被舍去了，造成结果的不一致这与我们最开始的理论一样。