强化学习DQN

DQN

针对Q-learning做出改进。原Q-learning的算法不能支持较大的Q表的查询和遍历，而DQN则直接将状态和动作当作神经网络的输入值，在分析后得到Q值；或者只输入状态值，输出动作值，从而根据Q-learning的原则进行动作的选择。

针对第二种进行分析，如何更新NN中的参数

1. 两个让DQN能够更好的学习的方法
   • Experience replay
     随机抽取经历进行学习，从而打乱经历之间的相关性
   • Fixed Q-targets
     建立两个NN从而分别更新不同的参数，Q现实：R+$\gamma \ast max{Q}^{\prime }$使用的参数为很久以前的参数更新一个NN，而Q估计：Q使用的参数为最新的参数，从而实现相关性的切断
2. 代码中和Q-learning有区别地方为

   	# 将现在的观测环境，动作，奖励以及下一个环境进行储存
   	RL.store_transition(observation, action, reward, observation_)
   

3. 搭建两个神经网络，一个用作实时更新，另一个落后更新。隔一段时间再把实时更新的参数传递给落后更新的参数

   	# tensorflow r1.2版本
   	# ------------------ all inputs ------------------------
   	# 定义所有输入参数
       self.s = tf.placeholder(tf.float32, [None, self.n_features], name='s')  # input State
       self.s_ = tf.placeholder(tf.float32, [None, self.n_features], name='s_')  # input Next State
       self.r = tf.placeholder(tf.float32, [None, ], name='r')  # input Reward
       self.a = tf.placeholder(tf.int32, [None, ], name='a')  # input Action
   
       w_initializer, b_initializer = tf.random_normal_initializer(0., 0.3), tf.constant_initializer(0.1)
   
       # ------------------ build evaluate_net ------------------
       with tf.variable_scope('eval_net'):
           e1 = tf.layers.dense(self.s, 20, tf.nn.relu, kernel_initializer=w_initializer,
                                bias_initializer=b_initializer, name='e1')
           self.q_eval = tf.layers.dense(e1, self.n_actions, kernel_initializer=w_initializer,
                                         bias_initializer=b_initializer, name='q')
   
       # ------------------ build target_net ------------------
       # target_net需要和evaluate_net定义成一样的结构，只是需要时所传参数不同而已
       with tf.variable_scope('target_net'):
           t1 = tf.layers.dense(self.s_, 20, tf.nn.relu, kernel_initializer=w_initializer,
                                bias_initializer=b_initializer, name='t1')
           self.q_next = tf.layers.dense(t1, self.n_actions, kernel_initializer=w_initializer,
                                         bias_initializer=b_initializer, name='t2')
   

4. memory存储管理

   	def store_transition(self, s, a, r, s_):
   		# 如果不存在memory_counter属性，则将memory_counter置0
           if not hasattr(self, 'memory_counter'):
               self.memory_counter = 0
           # 存储数据一条状态数据
           transition = np.hstack((s, [a, r], s_))
           # replace the old memory with new memory
           # 先从上到下存储，满了之后从0开始覆盖
           index = self.memory_counter % self.memory_size
           self.memory[index, :] = transition
           self.memory_counter += 1
   

5. 根据概率选择action
6. 为了阶段性地将训练的最新的参数更新到另一个target_net中，需要一个赋值操作

   	# 因为前期已经将参数添加到对应的collection中，所以直接get_collection就好
   	t_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='target_net')
       e_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='eval_net')
   
       with tf.variable_scope('hard_replacement'):
           self.target_replace_op = [tf.assign(t, e) for t, e in zip(t_params, e_params)]
   

7. 训练函数

   	# 摘抄自莫烦python==================
   	def learn(self):
       # 检查是否替换 target_net 参数
       if self.learn_step_counter % self.replace_target_iter == 0:
           self.sess.run(self.replace_target_op)
           print('\ntarget_params_replaced\n')
   
       # 从 memory 中随机抽取 batch_size 这么多记忆
       if self.memory_counter > self.memory_size:
           sample_index = np.random.choice(self.memory_size, size=self.batch_size)
       else:
           sample_index = np.random.choice(self.memory_counter, size=self.batch_size)
       batch_memory = self.memory[sample_index, :]
   
       # 获取 q_next (target_net 产生了 q) 和 q_eval(eval_net 产生的 q)
       q_next, q_eval = self.sess.run(
           [self.q_next, self.q_eval],
           feed_dict={
               self.s_: batch_memory[:, -self.n_features:],
               self.s: batch_memory[:, :self.n_features]
           })
   
       # 下面这几步十分重要. q_next, q_eval 包含所有 action 的值,
       # 而我们需要的只是已经选择好的 action 的值, 其他的并不需要.
       # 所以我们将其他的 action 值全变成 0, 将用到的 action 误差值 反向传递回去, 作为更新凭据.
       # 这是我们最终要达到的样子, 比如 q_target - q_eval = [1, 0, 0] - [-1, 0, 0] = [2, 0, 0]
       # q_eval = [-1, 0, 0] 表示这一个记忆中有我选用过 action 0, 而 action 0 带来的 Q(s, a0) = -1, 所以其他的 Q(s, a1) = Q(s, a2) = 0.
       # q_target = [1, 0, 0] 表示这个记忆中的 r+gamma*maxQ(s_) = 1, 而且不管在 s_ 上我们取了哪个 action,
       # 我们都需要对应上 q_eval 中的 action 位置, 所以就将 1 放在了 action 0 的位置.
   
       # 下面也是为了达到上面说的目的, 不过为了更方面让程序运算, 达到目的的过程有点不同.
       # 是将 q_eval 全部赋值给 q_target, 这时 q_target-q_eval 全为 0,
       # 不过 我们再根据 batch_memory 当中的 action 这个 column 来给 q_target 中的对应的 memory-action 位置来修改赋值.
       # 使新的赋值为 reward + gamma * maxQ(s_), 这样 q_target-q_eval 就可以变成我们所需的样子.
       # 具体在下面还有一个举例说明.
   
       q_target = q_eval.copy()
       batch_index = np.arange(self.batch_size, dtype=np.int32)
       eval_act_index = batch_memory[:, self.n_features].astype(int)
       reward = batch_memory[:, self.n_features + 1]
   
       q_target[batch_index, eval_act_index] = reward + self.gamma * np.max(q_next, axis=1)
   
       """
       假如在这个 batch 中, 我们有2个提取的记忆, 根据每个记忆可以生产3个 action 的值:
       q_eval =
       [[1, 2, 3],
        [4, 5, 6]]
   
       q_target = q_eval =
       [[1, 2, 3],
        [4, 5, 6]]
   
       然后根据 memory 当中的具体 action 位置来修改 q_target 对应 action 上的值:
       比如在:
           记忆 0 的 q_target 计算值是 -1, 而且我用了 action 0;
           记忆 1 的 q_target 计算值是 -2, 而且我用了 action 2:
       q_target =
       [[-1, 2, 3],
        [4, 5, -2]]
   
       所以 (q_target - q_eval) 就变成了:
       [[(-1)-(1), 0, 0],
        [0, 0, (-2)-(6)]]
   
       最后我们将这个 (q_target - q_eval) 当成误差, 反向传递会神经网络.
       所有为 0 的 action 值是当时没有选择的 action, 之前有选择的 action 才有不为0的值.
       我们只反向传递之前选择的 action 的值,
       """
   

---

DoubleDQN

对比DQN中的公式Q现实：
$Q_{max}$是selected_q_next = np.max(q_next, axis=1) # the natural DQN而这其中的q_next是从target_net中得到的，而这个值会有误差，所以将误差也同时做了最大化，从而导致了overestimate
针对DoubleDQN
想法是引入另一个神经网络来消除一些误差影响，而DQN本身就有两个神经网络，所以可以利用其中的evaluate_net来估计q_next中的最大动作值

	max_act4next = np.argmax(q_eval4next, axis=1) # the action that brings the highest value is evaluated by q_eval
    selected_q_next = q_next[batch_index, max_act4next]  # Double DQN, select q_next depending on above actions

其中的q_eval4next从evaluate_net中得到，用于从q_next中做估计，而q_next从target_net中得到的

最后将这个selected_q_next传给了q_target[batch_index, eval_act_index] = reward + self.gamma * selected_q_next

---

Prioritized Experience Replay (DQN)

在随机提取记忆的时候，按照重要程度进行抽样
考察重要程度的标准为TD-error，如果TD-error越大，则表示误差越大，越需要学习，而这个值是由Q现实-Q估计得来的。那么怎么从这个值得到优先级呢，就涉及到一个算法SumTree，参考link

	 while True:     # the while loop is faster than the method in the reference code
            cl_idx = 2 * parent_idx + 1         # this leaf's left and right kids
            cr_idx = cl_idx + 1
            if cl_idx >= len(self.tree):        # reach bottom, end search
                leaf_idx = parent_idx
                break
            else:       # downward search, always search for a higher priority node
                if v <= self.tree[cl_idx]:
                    parent_idx = cl_idx
                else:
                    v -= self.tree[cl_idx]
                    parent_idx = cr_idx

---

Dueling DQN

相比标准的DQN，Dueling DQN对网络结构做出了调整，将原来的输出Q值的网络做了拆分和合并

根据公式，将Q值分解为state值和每个action对state产生影响的advantage，并不是每个动作都会对state产生很大影响的

在tensorboard中看到的内容如下

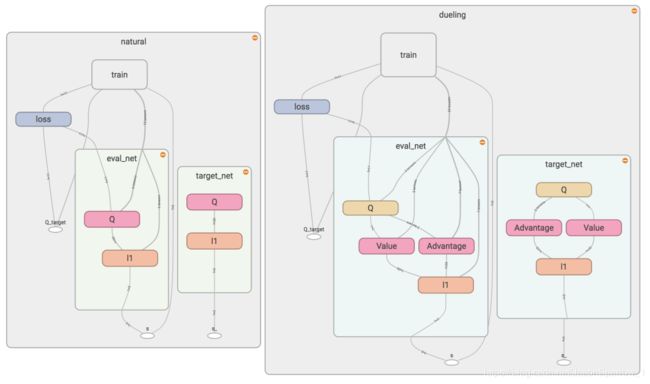
代码部分只对build_net部分做了修改：

	# Dueling DQN
    with tf.variable_scope('Value'):
        w2 = tf.get_variable('w2', [n_l1, 1], initializer=w_initializer, collections=c_names)
        b2 = tf.get_variable('b2', [1, 1], initializer=b_initializer, collections=c_names)
        self.V = tf.matmul(l1, w2) + b2

    with tf.variable_scope('Advantage'):
        w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
        b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
        self.A = tf.matmul(l1, w2) + b2

    with tf.variable_scope('Q'):
        out = self.V + (self.A - tf.reduce_mean(self.A, axis=1, keep_dims=True))
        # Q = V(s) + A(s,a)