并行遗传算法解决TSP问题

并行遗传算法解决TSP问题

一、问题描述

旅行商问题(TSP)可简单描述为：一位销售商从n个城市中的某一城市出发，不重复地走完其余n-1个城市并回到原出发点，在所有可能路径中求出路径长度最短的一条。旅行商的路线可以看作是对n个城市设计的一个环形，或者是对一列n个城市的排列。由于对n个城市所有可能的遍历数目可达(n-1)!个，解决这个问题需要O(n!)的计算时间。因此，如何高效且准确的求出使路径最短的n个城市的排列，成为了这个问题的关键。

二、实现算法

1、并行遗传算法简介

遗传算法以生物进化的过程作为模型，基本思想就是通过选择、交叉、变异得到下一代群体，如此反复，得到一个可以接受的解。核心是通过保持优秀个体有较大的概率被选择留在下一代，进行交叉、变异等操作，保持优秀个体的优越性，从而收敛至解空间。
然而遗传算法是一种概率搜索算法，其性能受种群规模、杂交和变异概率等控制参数的影响，而且有时会有收敛到局部最优解的现象。由于算法需要较大的种群规模，种群一代代进化，则需要不断的进行适应度函数计算，计算量相当大，因此，并行化遗传算法以提高算法的可靠性和效率是目前研究的主要内容。
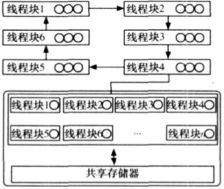
粗粒度并行遗传算法：在自然界中，物体的群体系由一些子群体组成，因此，可以将群体分为若干个子群体，每个子群体包含一些个体，每个子群体分配一个处理器，让它们互相独立地并行执行进化，每经过一定间隔，就把它们的最佳个体迁移到相邻的子群体中，这种现象称为“漂移”，这就是粗粒度并行化遗传算法。
从本质上讲，粗粒度并行遗传算法相比于串形遗传算法，在操作方法上有了根本改变。其中，如何进行“漂移”是影响算法效率的一个关键因素。

2、并行遗传算法求解TSP

a、算法设计

• 种群初始化。在TSP问题中，采用实数编码方式，实数编码为1到n的实数的随机排列。将种群初始化为多个子种群，并开辟相应个数的线程，每个线程负责一个子种群。初始化参数包括：子种群个数即线程数、城市个数、迭代次数、变异概率PM、保留概率PS。
• 适应度评价。TSP问题中，任意两个城市间的距离D(i，j)已知，每个染色体（即n个城市的随机排列）可计算出总距离。因此，可将一个随机全排列的总距离的倒数作为适应度函数，距离越短，适应度越好。
• 对各子种群进行选择、交叉、变异等遗传操作，并迭代m次。
  a、选择。将所有染色体的适应度按从大到小排序，按照保留概率PS保留适应度大的染色体，同时，将适应度小的染色体用大的代替。
  b、交叉。遗传算法中交叉方法有多种，本实验采用二交换启发交叉。
  c、变异。本实验通过随机选取染色体，并随机选取染色体的两个基因进行交换以实现变异。
• 将各子种群的最优解代替其相邻种群的差解。
• 重复第3、4步n次。
• 遍历各子种群中的最优解，找到一个全局最优解，作为最终解。

算法框图如下：

b、算法实现

(1)、读取各城市的序号和坐标，并计算城市间的距离，代码如下：

//初始化各城市间的距离
void init_dis()
{
  int i, j; 
  //读取城市坐标 
  ifstream in("/home/jjw/学习/GPU上机作业/遗传算法并行化/GA/source.txt");  
  if(in.is_open())
  {
    for (i = 0; i < nCities; i++)  
    {
      in >> nodes[i].num >> nodes[i].x >> nodes[i].y;  
    }
  }
  else
  {
    cout<<"open source.txt error"<float *temp_s = (float *)malloc( sizeof(float) * nCities * nCities );
  //计算城市间的距离
  for(int i=0;ifloat)INT_MAX; 
    for (j = i + 1; j < nCities; j++) 
    {
      temp_s[i * nCities + j] = temp_s[j * nCities + i] = sqrt(   
                    (nodes[i].x - nodes[j].x) * (nodes[i].x - nodes[j].x) +  
                    (nodes[i].y - nodes[j].y) * (nodes[i].y - nodes[j].y) );
    }
  } 
  cudaMemcpyToSymbol( data, temp_s, sizeof(float) * nCities * nCities);
  free( temp_s ); 
}

(2)、对序列1, 2, 3, 4 …… nCities随机排列，生成UNIT_NUM个不同的解，代码如下：

//1, 2, 3, 4 ...... nCities  
generate(temp.path, temp.path + nCities, GenByOne(0));  
//初始化UNIT_NUM个解，也就是群体 
for (int i = 0; i < UNIT_NUM; i++)   
{
   random_shuffle(temp.path, temp.path + nCities);  
   memcpy(&group[i], &temp, sizeof(temp)); 
}

(3)、在GPU中分配BlockDIm个block，每个block包含ThreadDIm个thread，即总共分配了BlockDIm×ThreadDIm个thread，每个线程负责计算EachBlock个排列组合，即将总群体分为BlockDIm×ThreadDIm个子群体，每个子群体里包含EachBlock组解。

(4)、计算各子群体中各组解的长度，代码如下：

__global__ void InitLength(unit *dataIn)
{
  int thread = blockIdx.x * ThreadDIm + threadIdx.x;
  int index = thread * EachBlock;

  for (int i = 0;i < EachBlock;i++)
  {
    CalCulate_length(dataIn[index + i]);        
  }
}

(5)、对各子种群进行遗传算法操作，当全部子种群完成GEN_IN次遗传算法操作后，进行种群间的信息交流，代码如下：

for (int i1 = 0 ; i1 < GEN_OUT ; i1++)
{
   GA <<>>(d_in);
   Exchange <<>>(d_in);
}

遗传算法具体步骤如下：
a、对各子种群中的解进行排序。
b、按照概率PS，用种群中的优秀解代替差解。
c、将优秀解与差解进行交叉，以获取更优秀的解，同时保持种群的多样性，交叉方法采用二交换启发交叉，二交换启发交叉方法的基本思想如下：

• 选2个参加交配的染色体作为父代，以8个城市为例来说明这一过程,父代染色体为：
  A　＝　3　2　1　4　8　7　6　5
  B　＝　2　4　6　8　1　3　5　7
  SUM1＝42,SUM2＝40，SUM1、SUM2分别为这2种排法所走的距离总和。
• 随机选出初始城市，比如：选A中的3为两个父代的第1位置。
  A　＝　3　2　1　4　8　7　6　5
  B ＝　3　5　7　2　4　6　8　1
• 由于d(3，2)＞d(3，5)所以有：
  A　＝　×　5　2　1　4　8　7　6
  B　＝　×　5　7　2　4　6　8　1
• 由此规则计算可得：
  O　＝　3　5　7　6　8　2 4　1
• 本来是2个不同的解，现在得到了一个比两个解都优的解，不能让原来的两个解都等于现在的这个局部最优解，这样不利于下次交叉，用如下的方法改变另外一个解的路径，在随机一个位置，将其后的序列放到前面，比如m=3，
  那么变换后的B为：
  B　＝　6　8　2 4　1 3　5　7　

代码如下：

//旋转 m 位
__device__ void Rotate(int path[],int len, int m)
{
             if( m < 0 )  
             {
               return;  
             }  
             if (m > len)   
             {
               m %= len;  
             }  
             Reverse(path, 0, m -1);  
             Reverse(path, m, len -1);  
             Reverse(path, 0, len -1);
} 
__device__ void Reverse(int path[], int b, int e)  
{
             int temp;  
             while (b < e)   
             {
                temp = path[b];   
                path[b] = path[e];  
                path[e] = temp;     
                b++;  
                e--;  
             }  
}

d、交叉完毕后，以PM的概率在各群体中选择num个解，在每个解中随机选两个位置，交换这两个位置的值。
e、循环步骤（a-d）GEN_IN次后，对各自种群中的解再进行一次排序。
遗传算法代码如下：

__global__ void GA(unit *dataIn)
{
  int thread = blockIdx.x * ThreadDIm + threadIdx.x;
  int index = thread * EachBlock;
  for (int i2 = 0 ; i2 < GEN_IN ; i2++)
  {
    //排序
    quicksort(dataIn + index , EachBlock);
    //NUM1 = EachBlock * ( 1 - PS);  
    for (int j = 0; j <=  NUM1 - 1; j++)   
    {
      //选择
      memcpy(&dataIn[index + NUM2 + j], &dataIn[index + j], sizeof(unit));
    }  
    for (int jq = 0; jq < EachBlock / 2; jq++)   
    {
      //交叉
      Cross_group(dataIn[index + jq], dataIn[index + EachBlock - jq -1]);  
    } 
    //变异  
    Varation_group(&dataIn[index]);
  }
  //排序
  quicksort(dataIn + index , EachBlock);
}

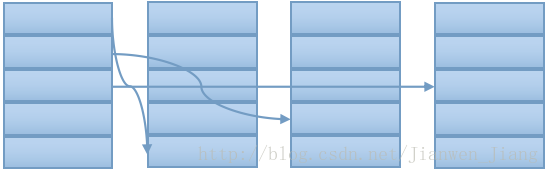
(6)、各子种群都完成遗传算法操作后，需要交流各子种群间的信息即“漂移”，漂移策略如下：

将各子种群中的最优解，分别取代其后Exchage个子种群中的倒数第一个、倒数第二个、倒数第Exchage个解。如下图所示：

(7)、重复上述步骤GEN_OUT次后，在所有解中，选取一个最优解作为最终解。选取方法如下：

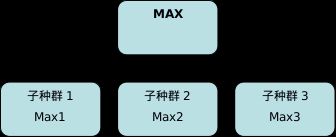
a、各子种群选取各自最大值。
b、在所有局部最大值中，选取一个全局最大值。
算法框图如下：

代码如下：

//bestarr数组用于保存各子种群的最优解
__global__ void FinalSort(unit *dataIn ,unit *bestarr)
{      
  int thread = blockIdx.x * ThreadDIm + threadIdx.x;
  int index = thread * EachBlock;
  unit min;
  min = dataIn[index];
  for (int cc = 1 ; cc < EachBlock ; cc++)
  {
     if ((dataIn[index + cc].length) < (min.length))
     {
        min = dataIn[index + cc];
     }
  }
  memcpy(&bestarr[thread], &min, sizeof(unit));
}
//在bestarr数组中保存的所有局部最优解中，找到一个全局最优解，保存到b_tmp中
__global__ void BestOne(unit *b_tmp ,unit *bestarr)
{
  for (int cc = 1 ; cc < ThreadDIm * BlockDIm ; cc++)
  {
     if ((bestarr[cc].length) < (bestarr[0].length))
     {
        bestarr[0] = bestarr[cc];
     }
  }
 memcpy(&b_tmp[0], &bestarr[0], sizeof(unit));
}

三、实验结果

1、实验环境

本实验的硬件环境GPU：NVIDIA GeForce 940M，CPU：Intel(R) Core(TM) i7-7700HQ CPU @2.8GHz。软件环境：Ubuntu16.04，CUDA9.0。
实验参数：城市数：99，群体规模：20000，遗传算法内部迭代次数：1，block数：5，每块block包含的线程数：200，每个子群体规模：20，“漂移”次数：10，保留概率：0.8，变异概率：0.1。

2、实验结果

迭代次数	1	2	3	4	10	20	50
1	4955.24	3637.58	2694.38	2442.57	1429.53	1236.53	1222.3
2	4836.48	3560.4	2950.3	2469.11	1396.38	1250.49	1226.14
3	4598.05	3635.66	2990.97	2414.92	1393.52	1248.09	1235.61
4	4863.91	3623.86	3014.36	2455.13	1419.2	1256.34	1218.61
5	4799.86	3643.52	2824.38	2496.79	1448.67	1254.01	1244.05
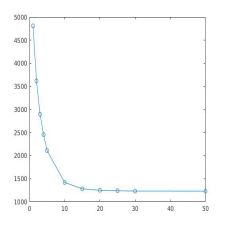
平均长度	4810.71	3620.20	2894.88	2455.70	1417.46	1249.09	1229.34

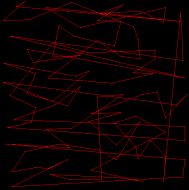
上面三张图分别为初始值、GEN_OUT=5、GEN_OUT=50时，对应的最优路径的连线。

由上图可以看出，GEN_OUT在15之后，对最终解的影响便很小，因此，在程序中将GEN_OUT设为15。GEN_OUT设为15后，将并行遗传算法与串行遗传算法相比较，在最终解相差不大的情况下，串行方式的运行时间是并行的10倍左右。

参考文献

http://blog.csdn.net/lalor/article/details/7704011
谭彩凤, 马安国, 邢座程. 基于CUDA平台的遗传算法并行实现研究[J]. 计算机工程与科学, 2009, 31(a01):68-72.

源代码

CUDA版本：
http://download.csdn.net/download/jianwen_jiang/10136380
OpenMP版本：
http://download.csdn.net/download/jianwen_jiang/10210777