【算法】图论(一) —— 基本图算法(BFS/DFS/强连通分量)

基本图算法

一、图的表示

对于图G=(V,E)，可以用两种表示方法表示，一种将图表示为邻接链表，另一种将图表示为邻接矩阵。这两种方法都既可以表示无向图，又可以表示有向图。
1. 邻接链表
邻接链表适用于稀疏图（边的条数 |E| 远小于 |V|2 的图）。邻接链表由一个包含|V|条链表的数组Adj构成，每个节点有一条链表。若G是无向图，则Adj[u]包含所有与u邻接的节点，所有邻接链表之和为2|E|；若G是有向图，则Adj[u]包含节点u所指向的所有节点，所有邻接链表之和为|E|。无论是有向图还是无向图，邻接链表表示法的存储空间需求为 Θ(V+E) 。邻接链表的一个潜在缺陷是无法快速判断一条边(u,v)是否在图中，唯一的方法是在邻接链表Adj[u]里搜索节点v。我们可以通过用散列表来替代链表加快边的搜索，但是缺陷是散列表的大小及散列函数难以确定，而且这种方法只在每条边的查询频率相同时效率最大。邻接矩阵也克服了这个缺陷，但需要更大的存储空间消耗。
2. 邻接矩阵
邻接矩阵对图G中的节点任意编号1,2,…,|V|，在编号后，用一个 |V|×|V| 的矩阵 A=(aij) 予以表示，该矩阵满足下述条件：

aij={10若(i,j)∈E其他

使用邻接矩阵表示一个图，无论图中边的数量为多少，其所需存储空间均为 Θ(V2) 。对于无向图，其邻接矩阵为一个对称矩阵，所以在某些应用中只需要存储对角线及其以上这部分邻接矩阵即可，从而将邻接矩阵的存储空间需求减少几乎一半。
3. 两种表示方法的比较
邻接矩阵表示比较简单，所以在图规模比较小的时候，可能更倾向于使用邻接矩阵表示，而且对于无向图来说，邻接矩阵的一个优势是每个记录项只需要一位空间。

二、广度优先搜索(BFS)

通常用于寻找特定源节点出发的最短路径距离，所以图通常为连通图。

广度优先搜索是最简单的图算法之一，是许多图算法模型的原型（Prim/Dijkstra等）。给定图G=(V,E)和一个可以识别的源节点s，广度优先搜索对图G中的边进行系统性的探索来发现可以从源节点s到达的所有节点。该算法能够计算从源节点s到每个可到达节点的距离(最少的边数)，同时生成一棵“广度优先搜索树”。该树以源节点s为根节点，包含所有可以从s到达的节点。对于每个从源节点s可以到达的节点v，在广度优先搜索树里从节点s到节点v的简单路径所对应的就是图G中从节点s到节点v的“最短路径”，即包含最少边数的路径。该算法对有向图和无向图同样适用。
在执行广度优先搜索的过程中将构造出一棵广度优先树。一开始该树只有根节点，即源节点s。在扫描已发现节点u的邻接链表时，每当发现一个未被发现的节点v，就将节点v和边(u,v)同时加入该树。以下为算法导论中的BFS伪代码，代码中为每个节点设置一个color属性，白色节点为未被发现节点，黑色节点和灰色节点均为发现节点，区别在于黑色节点的所有邻居节点都已经被发现，而灰色节点存在部分白色邻居节点。

BFS(G,s)
    // 初始化图中除源节点s外的所有节点属性
    for each vertex u in G.V-{s}
        u.color = WHITE // 未被发现
        u.d = INF       // 与源节点的距离为无限大
        u.pi = NIL      // 前驱节点/父节点为空
    // 初始源节点s属性
    s.color = GRAY
    s.d = 0
    s.pi = NIL
    Q = empty set      // 初始化灰色节点集
    ENQUEUE(Q, s)
    while Q is NOT an empty set
        u = DEQUEUE(Q)
        for each v in G.Adj[u]
            if v.color == WHILE
                v.color = GRAY
                v.d = u.d+1
                v.pi = u
                ENQUEUE(Q, v)
        u.color = BLACK 

算法复杂度分析：
每个节点的入队操作和出队操作最多均为1次，入队和出队的时间均为O(1)，因此对队列操作的总时间为O(V)。因为算法只在一个节点出队时才对该节点的邻接链表进行扫描，所以每个邻接链表最多只扫描一次。由于所有邻接链表的长度之和为 Θ(E) ，用于扫描邻接链表的总时间为O(E)。初始化操作的成本为O(V)，因此广度优先搜索的总时间为O(V+E)，即广度优先搜索的运行时间是图G的邻接链表大小的一个线性函数。

三、深度优先搜索(DFS)

通常作为另一个算法中的子程序，所以也常常用于不是连通图的图中。

深度优先搜索总是探索最近发现节点的子节点，知道探索到不存在子节点的节点v，则“回溯”到v的父节点，该过程一直持续到从源节点可以到达的所有节点都被发现为止。若还存在未发现节点，则从未发现节点任选一个作为新的源节点，重复同样过程，直到所有节点都被发现。
类似广度优先搜索算法，深度优先搜索在算法导论中同样使用颜色属性来指明节点状态，初始为白色，节点被发现为灰色，节点的邻接链表被扫描完成为黑色。同时，深搜中每个节点有两个时间戳：第一个时间戳v.d记录节点v第一次被发现的时间（涂上灰色的时候）；第二个时间戳v.f记录搜索完成对v的邻接链表扫描时间（涂上黑色的时候）。时间戳提供了图结构的重要信息，通常能够帮助推断深度优先搜索算法的行为。以下伪代码给出基本的深度优先算法。

DFS(G)
    for each vertex u in G.V
        u.color = WHITE
        u.pi = NIL
    time = 0  // 全局变量，用于计算时间戳
    for each vertex u in G.V
        if u.color == WHITE
            DFS-VISIT(G, u)
DFS-VISIT(G, u)
    time = time+1 //白色节点u刚刚被发现
    u.d = time
    u.color = GRAY
    for each v in G.Adj[u] // 探索边(u,v)
        if v.color = WHITE
            v.pi = u
            DFS-VISIT(G, v)
    u.color = BLACK
    time = time+1
    u.f = time

算法复杂度分析：
对于DFS(G)函数，排除对DFS-VISIT(G,u)的调用，其所需时间为 Θ(V) 。对于每一个节点 v∈V ，DFS-VISIT函数的调用次数为一次（当且仅当该节点为白色时，DFS-VISIT中将调用该函数的白色节点涂成灰色）。DFS-VISIT函数中遍历节点的邻接链表，对于所有节点来说，其操作成本为 Θ(E) ，因此深搜的运行时间为 Θ(V+E) 。
深搜中，节点的发现时间和完成时间具有括号化结构(parenthesis structure)，则发现时间和完成时间的历史记载形成规整的表达式，即所有括号都是正确的嵌套在一起，通过节点的两个时间戳，可以确定两个节点之间的关系（后代关系）。

四、强连通分量

强连通分量：对于有向图G=(V,E)，强连通分量是一个最大节点集合 C⊆V ，对于该集合中的任一节点对u和v，路径u->v和路径v->u同时存在，即节点u和节点v可以互相到达。
强连通分量是深度优先搜索的一个经典应用，许多针对有向图的算法都以此种分解操作开始。
寻找强连通分量需要对图G=(V,E)进行转置得到 GT=(V,ET) ，其中 ET={(u,v):(v,u)∈E} ，也就是对图G中的所有边进行反向得到。给定图G的邻接链表，得到其转置所需的时间为O(V+E)。可以看出图 G 和图 GT 中的强连通分量完全相同。算法导论中给出一个线性时间（ Θ(V+E) 时间）算法，通过两次深搜来计算有向图中的强连通分量。

STRONGLY-CONNECTED-COMPONENTS(G)
    call DFS(G) t compute finishing time u.f for each vertex u
    compute G^T
    call DFS(G^T), but in the main loop of DFS, consider the vertices in order of decreasing u.f (as computed above)
    output the vertices of each tree in the depth-first forest formed as a separate strongly connected component

该算法能够正确工作的关键在于：在转置图 GT 中，连接不同强连通分量的每条边都是从完成时间较早（第一次深搜所计算的完成时间）的分量指向完成时间较迟的分量，如下图所示，第一次深搜会构建一棵深度优先树，每个节点中记录该节点的发现时间/完成时间：

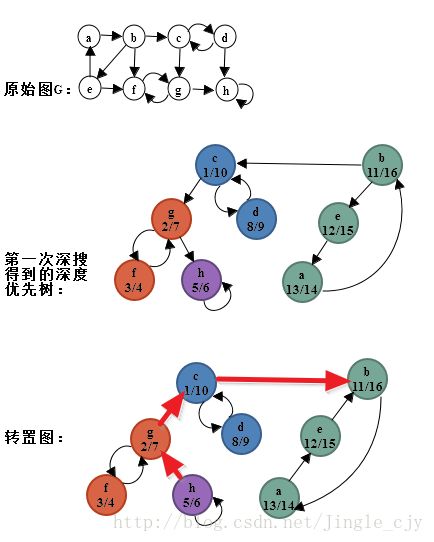
参考代码

[1] 广度优先搜索算法/深度优先搜索算法/强连通分量算法