主成分分析(Principa Component Analysis,PCA)
算法思想
在研一准备模式识别考试的时候,有这样一个总结我觉得能很清晰看到PCA在实际应用中的地位,见下图:

PCA可以对原始特征进行选择或变换,从而得到降维后的最能反映分类本质的特征,是最常用的一种降维方法,另外还有其他的方法,如因子分析(Factor Analysis)、独立成分分析(Independent Component Analysis,ICA)。
在PCA中,数据从原来的坐标系转换到了新的坐标系,新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向,第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差的方向。该过程一直重复,重复次数为原始数据中特征的数目。我们会发现,大部分方差都包含在最前面的几个新坐标轴中。因此,我们可以忽略余下的坐标轴,及对数据进行了降维处理。
算法步骤
基于最近重构性和最大可分性,能分别得到主成分分析的两种等价推导(可参见“西瓜书”对PCA的解析)
1.最近重构性
使用方差定义样本间间距:

并在降维之前将样例的均值归为0(demean),即
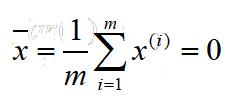
应用到PCA中,假设映射后的样本为Xp,则有:
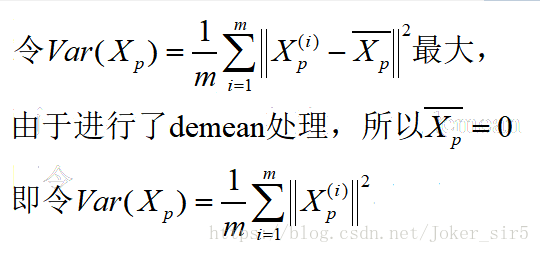
以二维为例,假设投影变换后得到的新坐标系为w=(w1,w2),其中wi是标准正交基,||wi||=1,wi^Twj=0(i不等于j),如图所示Xp即为投影后得到的样本
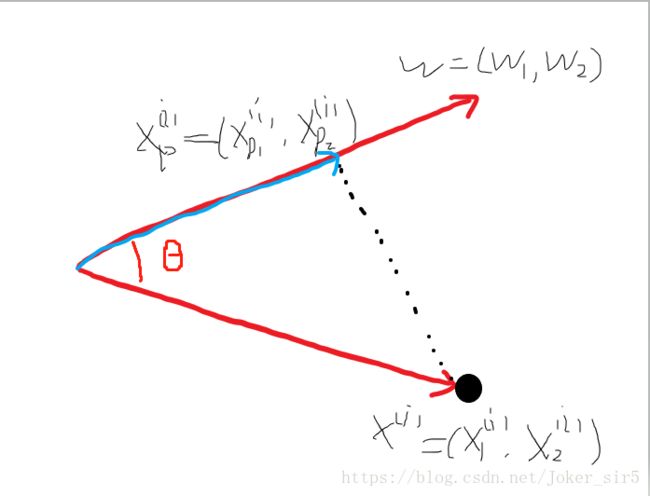
由向量运算可知,Xp可由X和w表示出来:
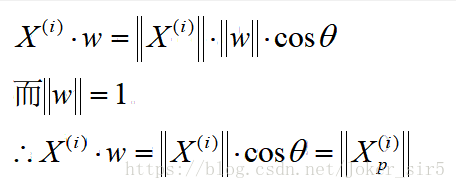
代入到上述Var(Xp)中可以得到最终的优化式子:
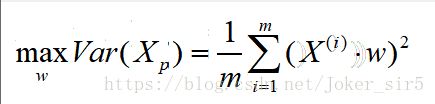
要优化上述式子可以使用梯度下降法求解,先求Var(Xp)的梯度:

使用梯度上升法,即可求得第一主成分,接着将数据在第一个主成分上的分量去掉,在新的数据上求第一主成分,即为原始数据的第二主成分,以此类推,若是高维数据,可以求出第三、第四…主成分


求出各主成分之后可以得到一个矩阵,每一行分别对应着第k个主成分:

接着Xw^T得到m*k的矩阵,该矩阵即为降维后的数据,将其送入具体的分类器中进行训练,会达到优良的效果(具体见代码)
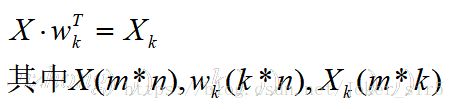
总结步骤:
1.对数据进行demean
2.利用梯度上升法优化式子
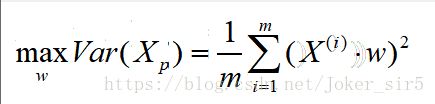
求出由前k个主成分组成的矩阵wk
3.用原始数据点乘wk得到降维后的矩阵Xk
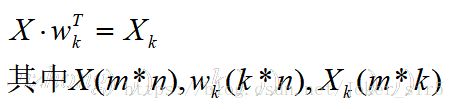
4.将Xk送入分类器中训练
2.最大可分性
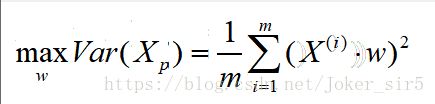
1中的优化函数也可以这样表示,加上标准正交基这个约束条件:
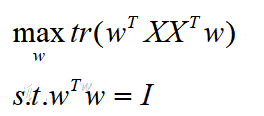
对上式使用拉格朗日乘数法可得:
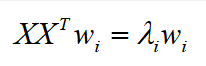
而XX^T为协方差矩阵,所以最终就是要对协方差矩阵进行特征值分解,将求得的特征值排序,再取前k的特征值对应的特征向量构成Wk,同上再利用X.dot(Wk.T)得到最终降维后的数据Xk,在送入对应的分类器中进行训练。
步骤总结
1.demean
2.计算协方差矩阵
3.计算协方差矩阵的特征值和特征向量
4.将特征值从大到小排序
5.选择最大的前k的特征值对应的特征向量组成Wk
6.Xk = X.dot(Wk.T)
7.将Xk送入分类器中进行训练
关键代码
1.最近重构性
1.demean
X - np.mean(X, axis=0)
2.梯度上升
# pca优化函数的梯度
def d_var(w, X):
return X.T.dot(X.dot(w)) * 2. / len(X)
# 将w变为单位向量
def direction(w):
return w / np.linalg.norm(w)
# 梯度上升法优化目标函数
def grad_component(X, initial_w):
w = direction(initial_w)
alpha = 0.01 # 步长
maxCycles = 1000 # 设置迭代的次数
for k in range(maxCycles):
gradient = d_var(w, X)
w = w + alpha * gradient
w = direction(w)
return w
# 求原始数据的前k个梯度,即求Wk
def pca_w(k, X):
X_pca = X.copy()
X_pca = demean(X_pca)
w_k = []
for i in range(k):
initial_w = np.random.random(X_pca.shape[1])
w = grad_component(X_pca, initial_w)
w_k.append(w)
X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w
return w_k
3.用原始数据点乘wk得到降维后的矩阵Xk
# 求降维后的矩阵Xk
def transform(X, w_k):
return X.dot(w_k.T)
4.将Xk送入分类器中训练
使用的数据是sklearn中的手写数据集(digits)(使用方法请翻阅以前的微博!),将由第3步得到的Xk送入knn分类器中训练
注意:X_train和X_test都需要进行降维
best_score = 0.0
best_k = 0
for k in range(1, X_train.shape[1]):
w_k = pca_w(k, X_train)
X_train_pca = transform(X_train, w_k)
X_test_pca = transform(X_test, w_k)
knn_clf.fit(X_train_pca, y_train)
if knn_clf.score(X_test_pca, y_test) > best_score:
best_score = knn_clf.score(X_test_pca, y_test)
best_k = k
print("best_score:", best_score)
print("best_k:", best_k)

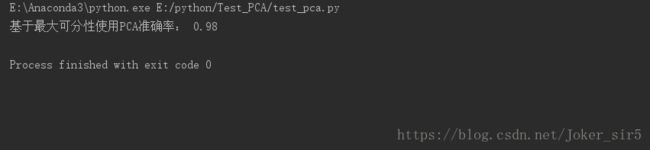
我使用网格搜索的方法,当数据由64维降到17维的时候准确率最高,可以达到0.98,对比于未使用pca的方式,准确率稍有提高
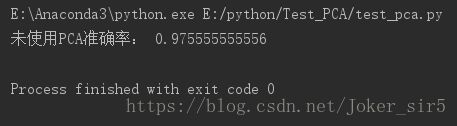
但是单从准确率来看0.98和0.9755…差别并不是很明显,那使用pca的最大的优势在哪里呢?我们找一个更大的数据集:mnist手写数据集,来看下效果
mnist.data.shape=(70000,784)
# X_train, y_train, X_test, y_test = load_mnist_data()
# knn_clf = KNeighborsClassifier()
start = time.clock()
knn_clf.fit(X_train, y_train)
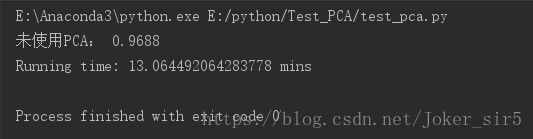
print("未使用PCA:", knn_clf.score(X_test, y_test))
end = time.clock()
print('Running time: %s mins' % float((end - start) / 60))
接着尝试着使用pca来降维,考虑到数据规模较大,且knn算法本身的速度限制,使用上述网格搜索的办法不太现实,我们直接使用sklearn自带的PCA方法,详情请参见PCA
其中有一个名为explained_variance_ratio_的Attributes,作用是
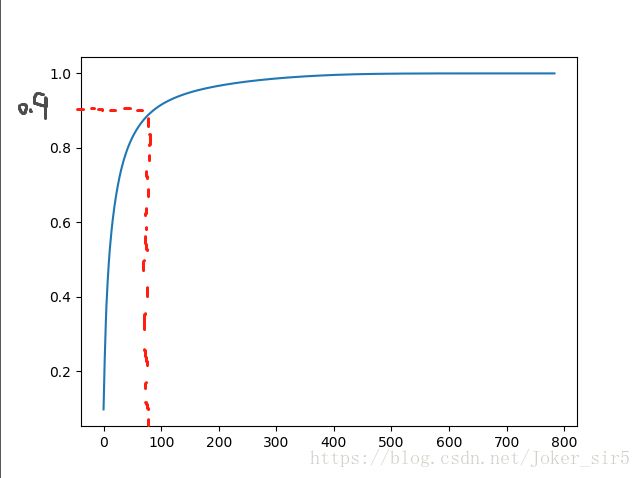
我们按横坐标是维数,纵坐标为累积方差百分比sum(Percentage of variance[:i+1]),将图形绘制出来(见下图),0-100图像变化显著,100=784变化逐渐平稳,这就表明约200个主成分之后对原始数据的影响就几乎可以忽略了,从图中也可以看到大约前90个主成分就可以表征90%的数据。也就是说我们可以将我们的原始数据从784维降到90维左右,就可以有很好表征。
pca = PCA(n_components=X_train.shape[1])
pca.fit(X_train)
plt.plot([i for i in range(X_train.shape[1])],
[np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
plt.show()
sklearn中的PCA方法有n_components这样一个属性,我们可以将其设置为我们想要降到的维数,更方便的,我们可以选择一个(0,1)的数,表示选择降到能表征原始数据的xx%的信息的维数,例如n_components=0.9

start = time.clock()
pca = PCA(0.9)
pca.fit(X_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
knn_clf.fit(X_train_pca, y_train)
print("使用PCA:", knn_clf.score(X_test_pca, y_test))
end = time.clock()
print('Running time: %s mins' % float((end - start) / 60))

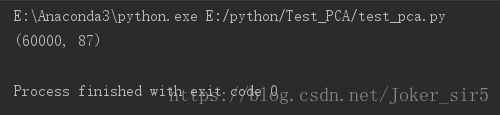
对比未使用PCA时的准确率,没有降维的准确率为0.9688,运行时间约13mins,而使用PCA保留原始数据90%的信息,将数据从784维降到了87维,不仅准确率提高到了0.9728,运行时间更是缩短到仅有约1.26mins,使用PCA降维的优势显而易见!
2.最大可分性
利用Numpy中寻找特征值及其对应的特征向量的模块linalg,其中的eig()方法可用于求解特征向量和特征值,可以很方便地实现PCA,使用sklearn中digits数据集,因上面已经用网格搜索的方式计算出将原始数据降到17维达最优,所以我这里就直接将17代入源码中,实验效果同梯度上升法求得结果:
def pca_cov(k, X):
X_pca = X.copy()
X_pca = demean(X_pca)
covMat = np.cov(X_pca, rowvar=0)
eigVals, eigVects = np.linalg.eig(np.mat(covMat))
eigValInd = np.argsort(eigVals)
eigValInd = eigValInd[:-(k+1):-1]
redEigVects = eigVects[:, eigValInd]
return redEigVects
if __name__ == "__main__":
X_train, y_train, X_test, y_test = load_sklearn_data()
w_k = pca_cov(17, X_train)
X_train_pca = X_train.dot(w_k)
X_test_pca = X_test.dot(w_k)
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_pca, y_train)
print("基于最大可分性使用PCA准确率:", knn_clf.score(X_test_pca, y_test))
总结
以上从两个不同的角度得到了主成分分析的两个种等价推导,并编写代码分别从底层实现了两种推导,从实验结果来分析,我们可以看到PCA降维的优势:降低数据的复杂性,这也在最终预测的准确率的提高,程序运行时间的大大缩短中有所体现。使用PCA将最能表征原始数据信息的若干个特征提取出来,将对数据影响不大的特征忽略掉,当然这也可以看做是一个降噪的过程,从而加强的有用信息,提高了代码的执行效率,最终得到的结果也表现优异。但是PCA也并非是一定需要的,这需要根据实际问题中数据而定,具体问题具体分析,若为加分析直接使用,PCApass掉的贡献率小的主成分往往可能含有对样本差异的重要信息,这样就会对最终的预测的结果产生影响,再者基于最大可分性中需要计算协方差矩阵,并求特征矩阵、特征向量,这其中自然会涉及到矩阵的运算,所示更高维的数据,这样计算复杂度也会随之增加。