NOIP提高组需要的一些模板【不定时更新】
感觉文章中出现问题或者看不懂的部分请评论提醒。
更新档案:
| time | events |
|---|---|
| 16/9/27 | 更新第一版 |
| 16/10/21 | 更新《基础排序算法》《基础图论算法》 |
| 16/10/22 | NOIP2016初赛 |
| 16/10/31 | 更新模板“高精度” |
| 16/11/14 | 更新模板“线段树” |
文件读入读出
假设题目名为“add”,那么文件夹名为“add”,c++程序名为“add.cpp”,读入文件名为“add.in”,输出文件名为“add.out”。
Focus:以上四个的拼写均不可有误,包括大小写差异。
#include 千万不要调试后就忘记修改文件读入读出了。
对拍
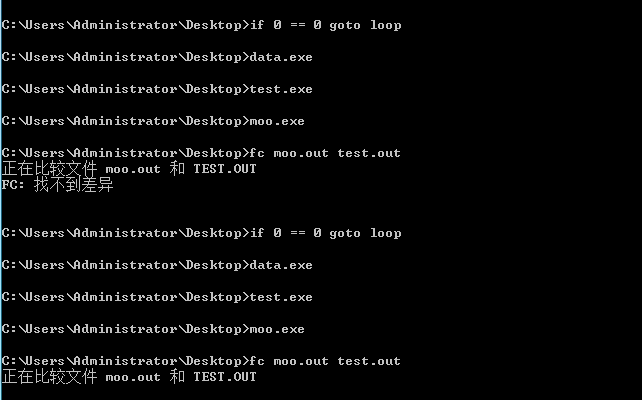
一般性的对拍可以借助命令行比较文件,需要两个输出的内容都在同一个文件夹下。
windows键+R,输入cmd,打开命令行,再根据下面内容依次输入:cd+当前文件夹地址->fc(比较)两个文件。

分别是相同与不同的情况。
比较高级的对拍需要造数据程序(data.exe),保证正确性的暴力对拍程序(test.exe)与测试程序(以moo.exe为例)。下面是对拍的代码,写在txt中再转成.bat即可。
:loop
data.exe
test.exe
moo.exe
fc moo.out test.out
if %errorlevel% ==0 goto loop
pause算法模板
1.基础排序算法的实现 (初赛要求)
首先是比较实用的所有 O(nlogn) 算法。
快速排序
快速排序的核心思想:
- 对于给定基底,将所有的元素按照与基底的大小关系重新分到该基底的左右部分。
快速排序的复杂度:
- O(nlogn)→O(n2) 。(若基底选取合适,每次排序之后都能劈掉一半区间,总递归只有 O(logn) 层;若选取不够合适,复杂度就退化到 O(n) 层(即每次只能劈掉一个数)。所以需要随机优化,使其基本稳定在 O(logn) 的复杂度)
- 快排是不稳定排序。(按照转移顺序,low指针小的先被转移到high指针,随后high指针变小,low指针变大,所以相对顺序一定会被改变掉)
快速排序的实现:
考虑用 O(n) 的复杂度实现按基底大小分配到左右区间的操作。这里推荐两种算法:
#include while(lowif(low//当前res[high]满足key值左侧,故扔给low位置
while(low=res[low])++low;
if(low1),qsort(low+1,R);
}
int main(){
int n;Rd(n);
for(int i=1;i<=n;i++)Rd(res[i]);
qsort(1,n);
for(int i=1;i<=n;i++)
printf("%d%c",res[i],i==n?'\n':' ');
} #include if(res[high]<=key)swap(&res[low++],&res[high]);
swap(&res[low],&res[R]);
qsort(L,low-1),qsort(low+1,R);
}
int main(){
int n;Rd(n);
for(int i=1;i<=n;i++)Rd(res[i]);
qsort(1,n);
for(int i=1;i<=n;i++)
printf("%d%c",res[i],i==n?'\n':' ');
}//该算法转自Codevs 快速排序的拓展运用:求序列第k大数,平均复杂度 O(n) 。
#include while(low=A[high])--high;
if(lowwhile(low=val)++low;
if(lowif(lowreturn qsort(low+1,R,k);
if(low>k)return qsort(L,low-1,k);
return low;
}
int main(){
srand(time(NULL));
int n,k;
scanf("%d %d %d",&n,&A[1],&k);
for(int i=2;i<=n;i++)
A[i]=1LL*A[i-1]*A[i-1]%P;
printf("%d\n",A[qsort(1,n,k)]);
return 0;
} 归并排序
归并排序的核心思想:
- 分治地使左右两个区间有序,通过两对有序数据的整合,可以得到理论下界复杂度算法。
归并排序的复杂度:
- O(nlogn) 。(由于每次一定会从中间劈开,所以一定只有 O(logn) 层)
- 有 O(n) 的辅助空间复杂度。
- 归并排序是稳定算法。(每层处理的时候,都是先将前面的相同元素放在前面的元素,即对于这一层是维护了左右序列的相对位置的。由于分治特性,所以每一层都是顺便维护的,所以是稳定的)
归并排序的实现:
#include 归并排序的拓展运用:求逆序对个数。
#include 堆排序
堆排序的核心思想:
- 维护一种二叉树数据结构:(小顶)堆,使得对于节点node,其父亲节点node/2,左右儿子节点node*2(+1),都满足当前层节点的数大于(小于)下层的数,小于(大于)上层的数。
堆排序的复杂度:
- 每次操作的平均复杂度是 O(logn) 。这个复杂度是因为二叉树的性质。
- 堆排序是不稳定排序。
堆排序的实现:
#include //小顶堆
if(heap[nxt]pos])swap(&heap[pos],&heap[nxt]);
else break;
pos=nxt;
}
}
}q;
int main(){
int n;Rd(n);
for(int i=1,x;i<=n;++i)Rd(x),q.push(x);
for(int i=1;i<=n;i++){
printf("%d",q.top());
putchar(i==n?'\n':' ');
q.pop();
}
} 四个基本排序分别为计数排序、选择排序、插入排序、冒泡排序,除计数排序的复杂度为 O(num) ,其余排序的复杂度均为 O(n2) 。
基数排序
基数排序的核心思想:
- 计数排序优化。按照每一数位的数值大小进行计数排序。
基数排序的复杂度:
- O(nK) , K 指的是最长位数。
- 基数排序有 O(nK) 的附加空间复杂度。
- 基数排序无法对含负数的序列进行直接处理,需要对每一个数都加上一个极大值。
- 基数排序是稳定排序。
基数排序的实现:
#include base*=10){
for(int j=0;j0;
for(int j=1;j<=n;j++){
int step=a[j]/base%10;
s[step][++sz[step]]=a[j];
}
int tot=0;
for(int j=0;jfor(int k=1;k<=sz[j];k++)
a[++tot]=s[j][k];
}
for(int i=1;i<=n;i++)
printf("%d%c",a[i],i==n?'\n':' ');
} 2.基础图论算法的实现 (部分初赛要求)
- 注意初赛一般不会考到最短路算法中的优化算法。
Dijkstra
- Dijkstra是单源最短路算法,即求该点到其他点的最短路径值。要求图中不存在负权边(如果带负权边那么这个更新的算法正确性就不能保证,因为可能经过一条负权边,使得之前已经认为最优的解反而不优)。
- 算法的实现如同“辐射网”:从当前已经是最短路径的点开始向外不断更新,直到全部更新完或者终点已经被更新。
Dijkstra的实现:
#include static const int M=1005;
int n,m,G[M][M],dis[M];
bool used[M];
void Dijkstra(int st){//暴力O(n^2)的实现
memset(dis,-1,sizeof(dis));
memset(used,0,sizeof(used));
dis[st]=0;
int u=-1;
while(true){
u=-1;
for(int i=1;i<=n;i++)
if(~dis[i]&&!used[i]&&(u==-1||dis[i]if(u==-1)break;
used[u]=true;
for(int v=1;v<=n;v++)
if(~G[u][v]&&!used[v]&&(dis[v]==-1||dis[v]>dis[u]+G[u][v]))
dis[v]=dis[u]+G[u][v];
}
}
int main(){
Rd(n),Rd(m);
memset(G,-1,sizeof(G));
for(int i=1,u,v,w;i<=m;i++){
Rd(u),Rd(v),Rd(w);
G[u][v]=~G[u][v]?min(G[u][v],w):w;
}
Dijkstra(1);
printf("%d\n",dis[n]);
} #include q;
memset(dis,-1,sizeof(dis));
memset(used,0,sizeof(used));
q.push((node){st,0});dis[st]=0;
while(!q.empty()){
node now=q.top();q.pop();
if(now.u==gt)return now.dis;
if(used[now.u])continue;
used[now.u]=true;
for(int j=head[now.u];~j;j=Edges[j].nxt){
edge nxt=Edges[j];
if(used[nxt.v])continue;
if(dis[nxt.v]==-1||dis[nxt.v]>nxt.w+dis[now.u]){
dis[nxt.v]=nxt.w+dis[now.u];
q.push((node){nxt.v,dis[nxt.v]});
}
}
}
return -1;
}
int main(){
int n,m,st,gt,top=0;
Rd(n),Rd(m),Rd(st),Rd(gt);
memset(head,-1,sizeof(head));
for(int i=1,u,v,w;i<=m;i++){
Rd(u),Rd(v),Rd(w);
add_edge(u,v,w,top);
}
printf("%d\n",Dijkstra(st,gt));
} Bellman_Ford
- Bellman_Ford是单源最短路算法。对边的权值没有限制,但若出现负环该算法可以判断是否存在负环。
- 算法原理:每次操作都对所有的边(显然是不必的,也就是SPFA算法的优化所在)进行松弛操作,显然每次至少会有一个点会被已经为最短路径点。那么最多只需要n-1次更新,我们就可以得到起点到所有点的最短路(否则起点到该点并未连通)。
- 判断负环的原理是在进行全部松弛操作之后,由于正常的图上每个点的最短路径已经被确定,所以第n次的松弛操作将不可能产生更新。显然唯一能产生更新的情况就是图上出现负环,导致最短路径值被无限更新下去。
Bellman_Ford的实现:
#include for(int j=1;j<=m;j++)
if(dis[G[j].v]>1ll*dis[G[j].u]+G[j].w)
dis[G[j].v]=dis[G[j].u]+G[j].w;
/*
进行第n次操作,即判负环操作。
bool flag=true;
for(int j=1;j<=m;j++)
if(dis[G[j].v]>1ll*dis[G[j].u]+G[j].w)
{flag=false;break;}
return flag;
*/
}
int main(){
Rd(n),Rd(m);
for(int i=1,u,v,w;i<=m;i++)
Rd(G[i].u),Rd(G[i].v),Rd(G[i].w);
Bellman_Ford(1);
if(dis[n]==inf)puts("-1");
else printf("%d\n",dis[n]);
} SPFA
SPFA算法优化在将Bellman_Ford的松弛点减少,即只将所有成功松弛过的点加入下一轮去松弛其他点的队列中,同时已经在松弛队列内的点不重复加入,就得到该算法了。同样的,如果有一点内加入松弛队列的次数大于n-1次,说明出现了负环。
SPFA的实现:
#include Floyd
- 务必要注意的是Floyd是一个非常特别的算法。
- Floyd是多源最短路算法,即求任意两点之间的最短距离,一般要求非负边。算法原理
- Floyd非常容易上手,只需要记住中间点的选取一定要放在三层for的最外层即可。Floyd其实就是dp,所以它满足无后向性,并且由于这个性质,我们可以和其他的算法一起套用,譬如说倍增+Floyd:POI2010_Hamsters
Floyd的实现:
#include Kruskal
- 最小生成树算法。算法思路是按照边权大小合并,当满足所有节点已经构成树时,此时求出的最小生成树就是最优的(最小生成树的性质:当边权不等时,该图的最小生成树唯一。同理,最多只会替换掉相同边权的边,而不会对最小生成树的大小产生影响)。由于在合并区间的时候采用并查集合并,所以复杂度在忽略对边排序的情况下,复杂度逼近理论下线 O(m) 。
Kruskal的实现:
#include int n,m,fa[M];
int getfa(int x){return fa[x]==x?x:fa[x]=getfa(fa[x]);}
int Kruskal(){
int sum=0;
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++){
int u=Edges[i].u,v=Edges[i].v;
u=getfa(u),v=getfa(v);
if(u!=v){
sum+=Edges[i].w;
fa[v]=u;
}
}
return sum;
}
int main(){
Rd(n),Rd(m);
for(int i=1,u,v,w;i<=m;i++){
Rd(u),Rd(v),Rd(w);
Edges[i]=(edge){u,v,w};
}
sort(Edges+1,Edges+m+1);
printf("%d\n",Kruskal());
} Prim
- 讲真……Prim算法就是Dijkstra算法的最小生成树版解法。所以初赛可能会考 O(n2) 复杂度的Prim。然后在求MST算法中不推荐Prim的……时空复杂度都不太好。
- 算法思路中有个地方要注意的是,当前dis值更新的不是最短路径值,而是连向这个点的边的边权。
Prim算法的 O(n2) 实现:
#include 数据结构模板
1.高精度BIgInteger的实现
通常根据不同的题目,高精要支持下列部分操作:
- 高精读入,输出。
- 高精度间比较。
- 高精与高精之间四则运算。
- 高精与低精之间四则运算。
当然通常来说,我们不需要支持负数高精。下面代码给出的是封装在struct结构体内的BigInteger,实际操作时不一定要写成面向对象的形式,只需要其中几个操作即可(各位自取自需)。
高精加法测试 | 高精减法测试 | 高精乘法测试 | 高精除法测试 | 低精除法测试
char str[1005];
struct BigInt{
static const int M=1005,P=10000;
#define clear(x,val) memset(x,val,sizeof(x))
int num[M],len;
BigInt(){clear(num,0),len=1;}
void read(){
scanf("%s",str);
len=0;
int sz=strlen(str);
for(int i=sz-1;i>=0;i-=4){
num[len]=0;
for(int j=max(0,i-3);j<=i;j++)
num[len]=(num[len]<<3)+(num[len]<<1)+(str[j]^48);
++len;
}
while(len>1&&!num[len-1])--len;
}
void print(){
printf("%d",num[len-1]);
for(int i=len-2;i>=0;i--)printf("%04d",num[i]);
putchar('\n');
}
bool operator < (const BigInt &cmp)const{
if(len!=cmp.len)return lenlen;
for(int i=len-1;i>=0;i--)
if(num[i]!=cmp.num[i])return num[i]return false;
}
bool operator > (const BigInt &cmp)const{return cmp<*this;}
bool operator <= (const BigInt &cmp)const{return !(cmp<*this);}
bool operator != (const BigInt &cmp)const{return cmp<*this||*thisbool operator == (const BigInt &cmp)const{return !(cmp<*this||*thisconst int &p){
BigInt B;B=*this;
B.num[0]+=p;
int step=0;
while(B.num[step]>=P){
B.num[step+1]++;
B.num[step]-=P;
++step;
}
while(B.num[B.len])++B.len;
return B;
}
BigInt operator + (const BigInt &A)const{
BigInt B;
B.len=max(A.len,len);
for(int i=0;ilen;i++){
B.num[i]+=num[i]+A.num[i];
if(B.num[i]>=P){
B.num[i]-=P;
B.num[i+1]++;
}
}
while(B.num[B.len])++B.len;
return B;
}
BigInt operator - (const int &p){//保证非负
BigInt B;B=*this;
B.num[0]-=p;
int step=0;
while(B.num[step]<0){
B.num[step]+=P;
B.num[step+1]--;
++step;
}
while(B.len>1&&!B.num[B.len-1])--B.len;
return B;
}
BigInt operator - (const BigInt &A)const{
BigInt B;
B.len=max(A.len,len);
for(int i=0;ilen;i++){
B.num[i]+=num[i]-A.num[i];
if(B.num[i]<0){
B.num[i]+=P;
B.num[i+1]--;
}
}
while(B.len>1&&!B.num[B.len-1])--B.len;
return B;
}
BigInt operator * (const int &p){
BigInt B;
B.len=len;
for(int i=0;i<len;i++){
B.num[i]+=num[i]*p;
if(B.num[i]>=P){
B.num[i+1]+=B.num[i]/P;
B.num[i]%=P;
}
}
while(B.num[B.len])++B.len;
return B;
}
BigInt operator * (const BigInt &A)const{
BigInt B;
B.len=A.len+len-1;
for(int i=0;i<len;i++)
for(int j=0;jlen;j++){
B.num[i+j]+=num[i]*A.num[j];
if(B.num[i+j]>=P){
B.num[i+j+1]+=B.num[i+j]/P;
B.num[i+j]%=P;
}
}
while(B.num[B.len])++B.len;
return B;
}
BigInt operator / (const int &p){
BigInt B=*this;
for(int i=B.len-1;i>=0;i--){
if(i)B.num[i-1]+=B.num[i]%p*P;
B.num[i]/=p;
}
while(B.len>1&&!B.num[B.len-1])--B.len;
return B;
}
BigInt operator / (const BigInt &A)const{
BigInt L,R,res;
if(*thisreturn res;
R=*this;
while(L<=R){
BigInt mid=(L+R)/2;
if((mid*A)<=*this){
res=mid;
L=mid+1;
}else R=mid-1;
}
return res;
}
}; 2.线段树的实现
我们以该入门例题进行讨论:
维护一个长度为 n(n≤105) 序列,现有以下四种操作:
- 在序列的pos位置增加val的权值 (val≤109) 。
- 在序列的[L,R]区间内都增加val的权值。
- 查询序列的pos位置的累积权值。
- 查询序列的[L,R]区间内的累积权值和。
保证操作交替进行。
- 代码中均以 Segment 的封装结构体来实现。
- 请务必注意的是,线段树的操作的平摊复杂度为严格且常数大的 O(logn) ,所以在实际实现中一般要对模板进行优化或者避免使用线段树。发生的惨剧请参见NOIP2012_day2_task2_classroom。
1) 【操作1+操作4】单点更新,区间查询。 测试
struct Segment{
static const int M=100005;
ll tree[M<<2];
void up(int p){tree[p]=tree[p<<1]+tree[p<<1|1];}
void build(int L,int R,int p){
if(L==R){Rd(tree[p]);return;}
int mid=L+R>>1;
build(L,mid,p<<1);
build(mid+1,R,p<<1|1);
up(p);
}
void update(int L,int R,int pos,int val,int p){
if(L==R){tree[p]+=val;return;}
int mid=L+R>>1;
if(pos<=mid)update(L,mid,pos,val,p<<1);
else update(mid+1,R,pos,val,p<<1|1);
up(p);
}
ll query(int L,int R,int l,int r,int p){
if(L==l&&R==r)return tree[p];
int mid=L+R>>1;
if(r<=mid)return query(L,mid,l,r,p<<1);
else if(l>mid)return query(mid+1,R,l,r,p<<1|1);
else return query(L,mid,l,mid,p<<1)+query(mid+1,R,mid+1,r,p<<1|1);
}
}Tree;2) 【操作2+操作3】区间更新+单点查询。 测试
- 不知道是不是有人直接联想到打标记的终极做法了,但其实并不必要。我们要利用线段树的每个节点:同样也是延迟更新,但是我们可以直接把权值留在完全覆盖的最上方的区间[L,R]而不必继续往下。
struct Segment{
static const int M=100005;
ll tree[M<<2];
void build(int L,int R,int p){
if(L==R){Rd(tree[p]);return;}
int mid=L+R>>1;
build(L,mid,p<<1);
build(mid+1,R,p<<1|1);
}
void update(int L,int R,int l,int r,int w,int p){
if(L==l&&R==r){tree[p]+=w;return;}
int mid=L+R>>1;
if(r<=mid)update(L,mid,l,r,w,p<<1);
else if(l>mid)update(mid+1,R,l,r,w,p<<1|1);
else{
update(L,mid,l,mid,w,p<<1);
update(mid+1,R,mid+1,r,w,p<<1|1);
}
}
ll query(int L,int R,int pos,int p){
if(L==R)return tree[p];
int mid=L+R>>1;
if(pos<=mid)return tree[p]+query(L,mid,pos,p<<1);
else return tree[p]+query(mid+1,R,pos,p<<1|1);
}
}Tree;3) 【操作2+操作4】区间更新+区间查询。 测试
- 请注意延迟标记在该层表示的意义是:该层已经使用过这个标记,并且它准备传到下一层。
(调了好久结果发现是读入挂的锅qvq)
struct Segment{
static const int M=200005;
struct Node{ll sum,add;}tree[M<<2];
void up(int p){
tree[p].sum=tree[p<<1].sum+tree[p<<1|1].sum;
}
void down(int L,int R,int p){
if(tree[p].add){
int mid=L+R>>1;
tree[p<<1].add+=tree[p].add;
tree[p<<1|1].add+=tree[p].add;
tree[p<<1].sum+=tree[p].add*(mid-L+1);
tree[p<<1|1].sum+=tree[p].add*(R-mid);
tree[p].add=0;
}
}
void build(int L,int R,int p){
tree[p].add=0;
if(L==R){Rd(tree[p].sum);return;}
int mid=L+R>>1;
build(L,mid,p<<1);
build(mid+1,R,p<<1|1);
up(p);
}
void update(int L,int R,int l,int r,int w,int p){
if(L==l&&R==r){
tree[p].add+=w;
tree[p].sum+=1ll*w*(R-L+1);
return;
}
down(L,R,p);
int mid=L+R>>1;
if(r<=mid)update(L,mid,l,r,w,p<<1);
else if(l>mid)update(mid+1,R,l,r,w,p<<1|1);
else{
update(L,mid,l,mid,w,p<<1);
update(mid+1,R,mid+1,r,w,p<<1|1);
}
up(p);
}
ll query(int L,int R,int l,int r,int p){
if(L==l&&R==r)return tree[p].sum;
down(L,R,p);
int mid=L+R>>1;
if(r<=mid)return query(L,mid,l,r,p<<1);
else if(l>mid)return query(mid+1,R,l,r,p<<1|1);
else return query(L,mid,l,mid,p<<1)+query(mid+1,R,mid+1,r,p<<1|1);
}
}Tree;- 关于用特殊
up()实现的线段树问题,参见这儿。