Sort多目标跟踪中的:指派问题与匈牙利解法
-
- 1、指派问题概述
- 2、指派问题性质
- 3、匈牙利法流程图
- 4、代码实现
有个蛮有意思的趣解,可帮助各位看官理解。
1、指派问题概述
有n项不同的任务,需要n个人分别完成其中的1项,每个人完成任务的时间不一样。于是就有一个问题,如何分配任务使得花费时间最少。
通俗来讲,就是n*n矩阵中,选取n个元素,每行每列各有1个元素,使得和最小,如图表示:
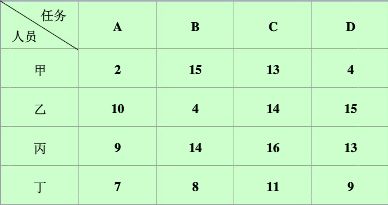
2、指派问题性质
最优解一般满足:若从矩阵的一行(列)各元素中分别减去该行(列)的最小元素,得到归约矩阵,其最优解与原矩阵的最优解相同。
3、匈牙利法流程图
4、代码实现
在多目标跟踪时,我们得到了上一帧的多个Bbox与这一帧的多个Bbox的IOU矩阵,需要找到最大IOU组合的索引对,这时我们使用匈牙利算法来计算。
import numpy as np
def linear_assignment(X):
"""
使用匈牙利算法解决线性指派问题。
"""
indices = _hungarian(X).tolist()
indices.sort()
# Re-force dtype to ints in case of empty list
indices = np.array(indices, dtype=int)
# Make sure the array is 2D with 2 columns.
# This is needed when dealing with an empty list
indices.shape = (-1, 2)
return indices
class _HungarianState(object):
"""
执行匈牙利算法的状态.
"""
def __init__(self, cost_matrix):
cost_matrix = np.atleast_2d(cost_matrix) # 2维矩阵
# 如果行大于列,算法则不能正常工作。需要转换过来。
transposed = (cost_matrix.shape[1] < cost_matrix.shape[0])
if transposed:
self.C = (cost_matrix.T).copy()
else:
self.C = cost_matrix.copy()
self.transposed = transposed # 记录这个标志
# 此时 m >= n.
n, m = self.C.shape
self.row_uncovered = np.ones(n, dtype=np.bool)
self.col_uncovered = np.ones(m, dtype=np.bool)
self.Z0_r = 0
self.Z0_c = 0
self.path = np.zeros((n + m, 2), dtype=int)
self.marked = np.zeros((n, m), dtype=int)
def _find_prime_in_row(self, row):
"""
Find the first prime element in the specified row. Returns
the column index, or -1 if no starred element was found.
"""
col = np.argmax(self.marked[row] == 2)
if self.marked[row, col] != 2:
col = -1
return col
def _clear_covers(self):
"""Clear all covered matrix cells"""
self.row_uncovered[:] = True
self.col_uncovered[:] = True
def _hungarian(cost_matrix):
"""
匈牙利算法。
解决经典指派问题的Munkres解答,返回最低成的索引对。
"""
state = _HungarianState(cost_matrix)
# 如果有一个维度为0,则不必进行了。
step = None if 0 in cost_matrix.shape else _step1
while step is not None:
step = step(state)
# Look for the starred columns
results = np.array(np.where(state.marked == 1)).T
# We need to swap the columns because we originally
# did a transpose on the input cost matrix.
if state.transposed:
results = results[:, ::-1]
return results
# 各个step返回下一步要调用的函数
def _step1(state):
# Step1: 找出矩阵中每行最小的元素值,并减去。
state.C -= state.C.min(axis=1)[:, np.newaxis]
# Step2: 找出零元素
for i, j in zip(*np.where(state.C == 0)):
if state.col_uncovered[j] and state.row_uncovered[i]:
state.marked[i, j] = 1
state.col_uncovered[j] = False
state.row_uncovered[i] = False
state._clear_covers()
return _step3
def _step3(state):
"""
如果有一行没对应到0,则转到 _step4
"""
marked = (state.marked == 1)
state.col_uncovered[np.any(marked, axis=0)] = False
if marked.sum() < state.C.shape[0]:
return _step4
def _step4(state):
"""
Find a noncovered zero and prime it. If there is no starred zero
in the row containing this primed zero, Go to Step 5. Otherwise,
cover this row and uncover the column containing the starred
zero. Continue in this manner until there are no uncovered zeros
left. Save the smallest uncovered value and Go to Step 6.
"""
# We convert to int as numpy operations are faster on int
C = (state.C == 0).astype(np.int)
covered_C = C * state.row_uncovered[:, np.newaxis]
covered_C *= state.col_uncovered.astype(dtype=np.int, copy=False)
n = state.C.shape[0]
m = state.C.shape[1]
while True:
# Find an uncovered zero
row, col = np.unravel_index(np.argmax(covered_C), (n, m))
if covered_C[row, col] == 0:
return _step6
else:
state.marked[row, col] = 2
# Find the first starred element in the row
star_col = np.argmax(state.marked[row] == 1)
if not state.marked[row, star_col] == 1:
# Could not find one
state.Z0_r = row
state.Z0_c = col
return _step5
else:
col = star_col
state.row_uncovered[row] = False
state.col_uncovered[col] = True
covered_C[:, col] = C[:, col] * (
state.row_uncovered.astype(dtype=np.int, copy=False))
covered_C[row] = 0
def _step5(state):
"""
Construct a series of alternating primed and starred zeros as follows.
Let Z0 represent the uncovered primed zero found in Step 4.
Let Z1 denote the starred zero in the column of Z0 (if any).
Let Z2 denote the primed zero in the row of Z1 (there will always be one).
Continue until the series terminates at a primed zero that has no starred
zero in its column. Unstar each starred zero of the series, star each
primed zero of the series, erase all primes and uncover every line in the
matrix. Return to Step 3
"""
count = 0
path = state.path
path[count, 0] = state.Z0_r
path[count, 1] = state.Z0_c
while True:
# Find the first starred element in the col defined by
# the path.
row = np.argmax(state.marked[:, path[count, 1]] == 1)
if not state.marked[row, path[count, 1]] == 1:
# Could not find one
break
else:
count += 1
path[count, 0] = row
path[count, 1] = path[count - 1, 1]
# Find the first prime element in the row defined by the
# first path step
col = np.argmax(state.marked[path[count, 0]] == 2)
if state.marked[row, col] != 2:
col = -1
count += 1
path[count, 0] = path[count - 1, 0]
path[count, 1] = col
# Convert paths
for i in range(count + 1):
if state.marked[path[i, 0], path[i, 1]] == 1:
state.marked[path[i, 0], path[i, 1]] = 0
else:
state.marked[path[i, 0], path[i, 1]] = 1
state._clear_covers()
# Erase all prime markings
state.marked[state.marked == 2] = 0
return _step3
def _step6(state):
"""
Add the value found in Step 4 to every element of each covered row,
and subtract it from every element of each uncovered column.
Return to Step 4 without altering any stars, primes, or covered lines.
"""
# the smallest uncovered value in the matrix
if np.any(state.row_uncovered) and np.any(state.col_uncovered):
minval = np.min(state.C[state.row_uncovered], axis=0)
minval = np.min(minval[state.col_uncovered])
state.C[np.logical_not(state.row_uncovered)] += minval
state.C[:, state.col_uncovered] -= minval
return _step4
