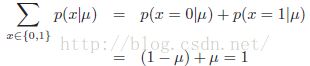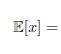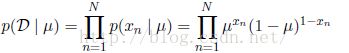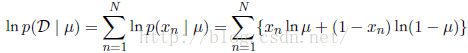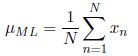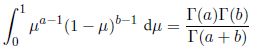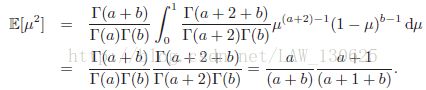【PRML读书笔记】2.概率分布（上）

概率分布

一、二元变量
1.简单的随机二元变量
        假设存在一个简单的随机二元变量x ∈{0,1}。例如在投掷硬币的过程中假设由于硬币的损坏是的正反两面的概率是不相等的，令正面为1，反面为0，那么x=1的概率用参数 μ来表示，即：

        其中μ大于等于0，小于等于1，且我们容易得出p(x=0|μ)=1-μ。从而我们得到x的概率分布可以表示为：

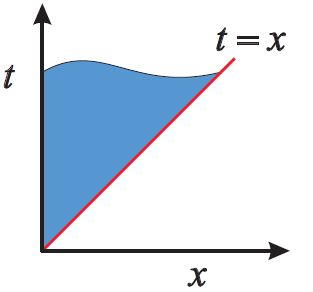
        上式即为伯努利分布（Bernoulli distribution）。下面我们通过简单的推导其满足归一化，以及其期望、方差和熵：

                                                                    

        假设现在有数据集D={x1，...，xN}，假设每次观测都是独立地从p(x|μ)中抽取的，因此我们可以构造关于μ的似然函数为：

        一般我们是对于μ的估计是通过求最大似然函数而得，而通过求最大似然函数的对数形式会更方便一些，并且它们之间是等价的，所以最大似函数的对数形式为：

        通过对上式对μ进行求导并令其为0，我们可以获得μ的最大似然估计值为：

        这也被称为样本均值（sample mean）。如果我们把数据集里x = 1（正面朝上）的观测的数量记作m，那么我们可以把上式写成下面的形式，而且我们发现在最大似然中，正面朝上的概率是数据集里正面向上的观测所占的比例。

        给定数据集规模N的条件下，x = 1的观测出现的数量m的概率分布。这被称为二项分布（binomial distribution），为了得到归一化系数，在N次抛掷中，我们必须把所有获
得m个正面朝上的方式都加起来，因此二项分布表示为：

          

        通过简单的推导得到二项分布的期望和方差，首先对μ进行求导并令其为零，可得到其期望，再次进行求导令其为0整理后可得μ平方的期望，根据相关公式即可得到方差：

2.贝塔分布（Beta distribution）

        Beta分布先验分布的定义为：

        其中a，b称之为超参数，它们控制着参数 μ的分布，T（）为gamma函数，其定义为：

        gamma函数部分确保了Beta分布是归一化的，证明如下：根据gamma函数的定义可得：

        令t=y+x，可得：

        交换积分顺序可得：

                      

          再令x=t μ，可得：

        从而我们可以得到：

        即为：

        接下来简单推导其期望与方差，根据期望的定义可得：

        根据上面归一化的推导以及gamma函数的性质，即可得到：

        接着对 μ的平方求期望，即为：

        根据公式：

        可得：

        关于 μ的后验分布可以通过Beta先验分布与二项分布的似然函数相乘以及归一化后而得，可以得到其分布形式如下：

        其中l=N-m，即对应于硬币“反面朝上”的样本数量。我们上述公式关于的函数形式与先验分布相同，这反映出先验关于似然函数的共轭性质。实际上，它仅仅是另一个Beta分布。通过与先验分布对比，我们可以得到它的归一化系数，可得：

        我们的目标是尽可能好地预测下一次试验的输出，那么在给定观测数据集D的情况下，必须估计x的预测分布。根据概率的加和规则和乘积规则，这个预测分布的形式为：

        使用上述后验分布公式作为p( μ|D)的后验分布以及Beta分布的期望，我们可以得到：

        考虑一个一般的贝叶斯推断问题，参数为，并且我们观测到了一个数据集D，由联合概率分布p(θ|D)描述，其结果为：

        其中：

        上述表明，在数据集产生的整个分布上θ的后验均值等于θ的先验均值。类似地，我们可以证明

        其主要过程为：根据概率乘积规则可得：

        由于方差是一个整数，因此这个结果表明，从平均来看后验方差小于先验差。后验均值的方差越大，这个方差的减小就越大。但是需要注意的是，这个结果只在平均情况下成立，对于一个特定的观测数据集，有可能后验方差大于先验方差。