Codevs 多米诺+覆盖题解
上一篇写了二分图匹配的匈牙利算法这篇当然是例题辣!
多米诺
题目描述 Description
一个矩形可以划分成M*N个小正方形,其中有一些小正方形不能使用。一个多米诺骨牌占用两个相邻的小正方形。试问整个区域内最多可以不重叠地放多少个多米诺骨牌且不占用任何一个被标记为无法使用的小正方形。
输入描述 Input Description
第一行有两个用空格隔开的正整数M和N。
第二行有一个正整数K,表示共有K个小正方形不能使用。输入数据保证K<=M*N。
以下K行每行有两个用空格隔开的数X和Y,表示第X行的第Y个小正方形不能使用。
输出描述 Output Description
输出最多能放多少个多米诺骨牌。
样例输入 Sample Input
3 3
2
1 1
2 2
样例输出 Sample Output
3
数据范围及提示 Data Size & Hint
对于30%的数据,M=1;
对于50%的数据,M<=2;
对于70%的数据,M<=3;
对于100%的数据,M<=50,N<=50。
覆盖
题目描述 Description
有一个N×M的单位方格中,其中有些方格是水塘,其他方格是陆地。如果要用1×2的矩阵区覆盖(覆盖过程不容许有任何部分重叠)这个陆地,那么最多可以覆盖多少陆地面积。
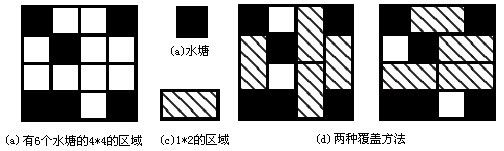
输入描述 Input Description
输入文件的第一行是两个整数N,M (1<=N,M<=100),第二行为一个整数K( K<=50),接下来的K行,每行两个整数X,Y表示K个水塘的行列位置。(1<=X<=N,1<=Y<=M)。
输出描述 Output Description
输出所覆盖的最大面积块(1×2面积算一块)。
样例输入 Sample Input
4 4
6
1 1
1 4
2 2
4 1
4 2
4 4
样例输出 Sample Output
4
为什么两个题放到一起呢?因为这可是codevs 的双倍经验!!!首先我们可以发现,这两个题几乎一模一样。。OK不扯淡了进入正题。
这两道题解题思路十分简单,难点在于怎么想。
我们对于每一个能覆盖的点(我是用的bool数组,能覆盖的是0),维护它的上下左右四个方块。不能覆盖的点当然直接就是0辣。维护完后,把每个点拆成左右两个跑一半匈牙利然后除以2就可以了。因为数据范围非常小,匈牙利就能够做到。如果碰到数据范围坑爹的题目,要么偏分,要么去学Dinic。。。。反正我不会。。。。至于为什么除以二,因为你每一个点都拆成了俩计算了两次自然要除以二咯。
下面是覆盖的标程
#include多米诺的标程
#includeif(j>1 && jif(mp[i][j-1]==0) V[(i-1)*n+j].push_back((i-1)*n+j-1);
if(mp[i][j+1]==0) V[(i-1)*n+j].push_back((i-1)*n+j+1);
if(mp[i-1][j]==0) V[(i-1)*n+j].push_back((i-2)*n+j);
if(mp[i+1][j]==0) V[(i-1)*n+j].push_back(i*n+j);
}
if(j==1)
{
if(mp[i][j+1]==0) V[(i-1)*n+j].push_back((i-1)*n+j+1);
if(mp[i-1][j]==0) V[(i-1)*n+j].push_back((i-2)*n+j);
if(mp[i+1][j]==0) V[(i-1)*n+j].push_back(i*n+j);
}
}
if(i==1)
{
if(j>1 && jif(mp[i][j-1]==0) V[(i-1)*n+j].push_back((i-1)*n+j-1);
if(mp[i][j+1]==0) V[(i-1)*n+j].push_back((i-1)*n+j+1);
//if(mp[i-1][j]==0) V[i-1)*n+j].push_back((i-2)*n+j);
if(mp[i+1][j]==0) V[(i-1)*n+j].push_back(i*n+j);
}
if(j==1)
{
if(mp[i][j+1]==0) V[(i-1)*n+j].push_back((i-1)*n+j+1);
//if(mp[i-1][j]==0) V[i-1)*n+j].push_back((i-2)*n+j);
if(mp[i+1][j]==0) V[(i-1)*n+j].push_back(i*n+j);
}
}
}
}
}
bool match(int x)
{
for(int i=0;ix].size();i++)
{
if(!use[V[x][i]])
{
if(dxpend[V[x][i]]==-1 || dxpend[V[x][i]])
{
dxpend[i+1]=x;
return true;
}
}
}
return false;
}
int hungray()
{
int tot=0;
memset(dxpend,-1,sizeof(dxpend));
for(int i=1;i<=sum;i++)
{
memset(use,0,sizeof(use));
if(!match(i)) tot++;
}
return tot/2;
}
int main()
{
scanf("%d%d%d",&m,&n,&k);
sum=n*m;
for(int i=1;i<=k;i++)
{
int a,b;
scanf("%d%d",&a,&b);
mp[a][b]=1;
}
make_tu();
cout<