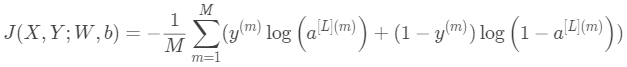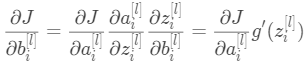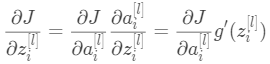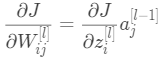机器学习系列(1):十分钟掌握深度神经网络的原理、推导与实现
“ 哎呀人工智能好像很火啊,神经网络又是啥,这里是机器学习系列第一篇,带你走进AI,那DNN了解一下(本文干货风哦)。”
图片挂了...贴个链接吧,大家可以到这看.
https://mp.weixin.qq.com/s?__biz=MzU4NTY1NDM3MA==&mid=2247483715&idx=1&sn=f81cb0764e1a4c2fc5aef75f94ea8215&chksm=fd86084ecaf18158c7c4c6446745596510c64de5080fa43407ad1bd68c82e02c01c277de3e03#rd
00 内容概览
机器学习系列(1):深度前馈神经网络--原理解释、公式推导及Python实现
深度神经网络的原理解释:
-
定义
-
变量约束
-
前向传播
-
反向传播
-
数据集
公式推导:
-
前向过程
-
BP算法
-
梯度下降
Python实现:
-
见文章内容
申明
本文原理解释及公式推导部分均由LSayhi完成,供学习参考,可传播;代码实现部分的框架由Coursera提供,由LSayhi完成,详细数据及代码可github查阅。
https://github.com/LSayhi/DeepLearning
微信公众号:AI有点可ai
01 原理解释
1.1 定义: 前馈神经网络,亦称多层感知机,网络的目标是近似一个目标映射 f ,记为y=f(x;θ)。 对于预测型神经网络来说,通过学习参数θ的值,使得函数 f 拟合因变量自变量之间的 映射关系;对于分类神经网络,学习参数θ的值,使映射 f 拟合各类别之间的边界。
-
神经网络模型由输入层、输出层、隐藏层及连接各层之间的权重(参数)组成。
-
“深度”是指 除去模型中输入层后网络的层数;
-
“前馈”是指 网络没有反馈的连接方式;
-
“网络”是指 它是由不同函数g所复合的。
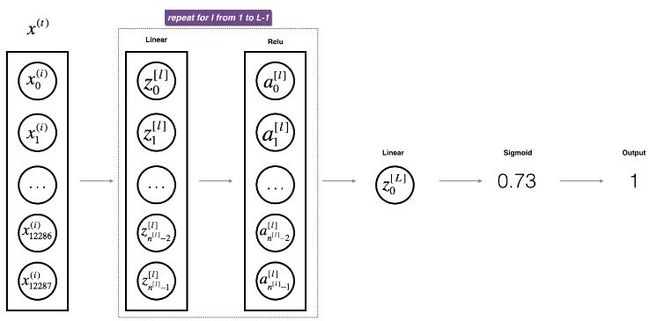
1.2 变量约束: 以一个输入层特征数为 n_x(=12888,n_x定义为输入层的单元数) ,L(=L-1+1,L定义为除去输入层的网络层数) 层,即隐藏层数为 L-1 的前馈神经网络为例,见figure 1。
-
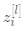 表示第
表示第 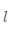 层第
层第 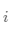 个线性单元,
个线性单元, 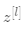 表示第
表示第 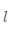 层所有线性单元
层所有线性单元 -
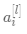 表示第
表示第 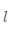 层第
层第 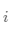 个激活单元,
个激活单元, 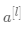 表示第
表示第 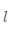 层所有激活单元
层所有激活单元 -
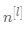 表示第
表示第 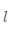 层单元的数目
层单元的数目
Figure 1
1.3 前向传播:前向传播指的是输入数据(集)从输入层到输入层的计算过程。在输入数据之前,需要先进行参数初始化,即随机生成![]() 矩阵,
矩阵,![]() 矩阵。然后每个层的单元根据
矩阵。然后每个层的单元根据![]() 矩阵和前一层的数据进行计算线性输出,再由激活函数非线性化,层叠往复,最后得到输出层的输出数据,称此过程为前向传播。
矩阵和前一层的数据进行计算线性输出,再由激活函数非线性化,层叠往复,最后得到输出层的输出数据,称此过程为前向传播。
1.4 反向传播:反向传播指的是当输出层计算出输出数据后,与数据集中对应的标签进行比对,求出损失(Loss,单个样本)和代价(损失的和,整个样本集),再求解参数![]() 和
和![]() 的偏导数,进而由梯度下降等方法更新参数
的偏导数,进而由梯度下降等方法更新参数![]() 和
和![]() ,当损失为0或者达到目标值时停止,由于求解参数
,当损失为0或者达到目标值时停止,由于求解参数![]() 和
和![]() 的偏导数是一个反向递推的过程,所以此过程也因此成为反向传播。
的偏导数是一个反向递推的过程,所以此过程也因此成为反向传播。
1.5 数据集: 数据集是用来训练和测试网络的数据的集合,包括训练集、开发集和测试集。一般来说,训练集用于训练网络达到最佳,开发集和测试集用来检验网络泛化性能。
02 公式推导
2.1 前向传播:
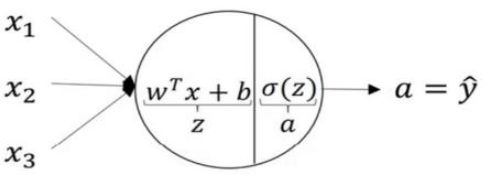
一个简单前向传播的例子,见figure 2。
Figure 2
一般的对于一个 ![]() 层的前馈网络,第
层的前馈网络,第 ![]() 层的线性函数实现
层的线性函数实现![]() 对M个样本向量化后,表示为
对M个样本向量化后,表示为![]() 那么
那么![]() ,其中g为激活函数,常见的激活函数有sigmoid、tanh、Relu等,
,其中g为激活函数,常见的激活函数有sigmoid、tanh、Relu等,![]() 。
。
特殊地,输入层![]() 另记为
另记为![]() ,输出层记为
,输出层记为![]() ,对M个样本向量化后为
,对M个样本向量化后为![]() 和
和![]() 。由此,只要给出
。由此,只要给出![]() ,由公式
,由公式![]() 和
和![]() 即可由前向后逐步求出
即可由前向后逐步求出![]() ,这就是前向传播的过程。
,这就是前向传播的过程。
2.2 损失和代价:
-
损失函数:对应于单个样本。
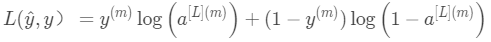
损失函数定义了度量神经网络输出层输出的数据与标签之间的差异值(即损失),其功能类似于均方误差函数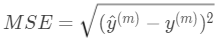 事实上,
事实上,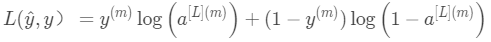 是交叉信息熵,最小化交叉信息熵也等效于最大似然准则(MLP),最小化交叉信息熵直观上可以认为和最小化误差相似,能够用来度量被比较对象的差异大小,但因均方误差函数的特点,在逻辑回归中很可能会导致收敛速度缓慢,并且代价函数不一定是凸函数,不一定能收敛于最小值,可能会收敛到某个非最小的极小值点,所以我们常用交叉信息熵代替均方误差。这里详细可参考个人笔记机器学习中的数学(1)--交叉信息熵
是交叉信息熵,最小化交叉信息熵也等效于最大似然准则(MLP),最小化交叉信息熵直观上可以认为和最小化误差相似,能够用来度量被比较对象的差异大小,但因均方误差函数的特点,在逻辑回归中很可能会导致收敛速度缓慢,并且代价函数不一定是凸函数,不一定能收敛于最小值,可能会收敛到某个非最小的极小值点,所以我们常用交叉信息熵代替均方误差。这里详细可参考个人笔记机器学习中的数学(1)--交叉信息熵
2.3反向传播
-
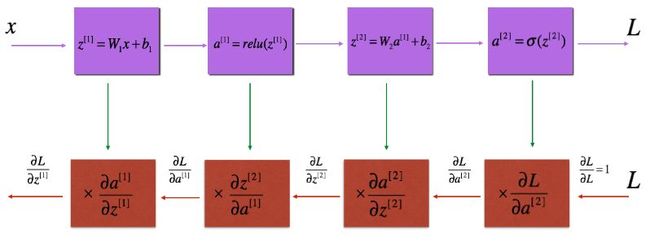
反向传播过程可由下图Figure 3表示:
Figure 3 : Forward and Backward propagation
网络的目标是使得![]() 最小,在数学上就是多变量函数求最值问题,首先想到的可能是求偏导数,然后另偏导数等于零,找到最小值点,得到对应参数W和b的值,此法称正规方程法,但是由于矩阵
最小,在数学上就是多变量函数求最值问题,首先想到的可能是求偏导数,然后另偏导数等于零,找到最小值点,得到对应参数W和b的值,此法称正规方程法,但是由于矩阵![]() 不一定可逆,所以我们使用梯度下降法来寻找最优的参数W和b。
不一定可逆,所以我们使用梯度下降法来寻找最优的参数W和b。
梯度下降法表示为:![]()
![]()
梯度下降法也需要求出代价函数关于参数W和b的偏导数,由求导数的链式法则可知,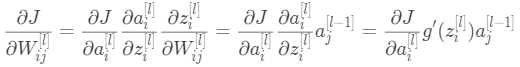 (1
(1
将③代入①和②,可知:
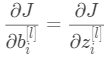 (5)
(5)
将式③、④、⑤矢量化,并记为![]()
![]() (7)
(7)![]() (8)
(8)
“![]() ∗”表示矩阵对应元素相乘,⑥式中的
∗”表示矩阵对应元素相乘,⑥式中的![]() ,推导过程如下,对于第
,推导过程如下,对于第![]() 层,应用链式法则
层,应用链式法则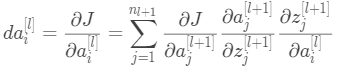
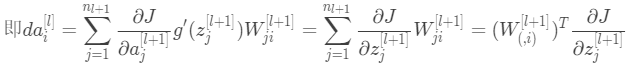
向量化后为:![]() 代入⑥,故⑥式可改写为:
代入⑥,故⑥式可改写为:![]() (9)
(9)
再对M个数据向量化:
![]() (11)
(11)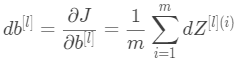 (12)
(12)![]() (13)
(13)
2.4 梯度下降:
由(10)、(11)、(12)、(13)便可以从输出层反向递推到第1层,得到关于参数W和b的所有偏导数,再应用梯度下降法,不断更新参数:![]()
![]()
就可以得到最佳的W和b参数,使得训练集的代价函数最小。注:梯度的方向是函数值上升最快的方向,因此梯度的负方向即是函数值下降最快的方向,应用梯度下降即是使函数在某个位置(W,b)沿最快的方向减小。
2.5 网络优化:
至此,网络的训练已经完成,可以在测试集上进行泛化测试。如果泛化的准确率不高,分析原因:
-
如果过拟合了,可以考虑增加数据集、正则化、dropout、适当减小网络层数L等
-
如果欠拟合了,可以考虑增加特征数量、增加网络层数、隐藏层神经元数目等
03 python实现
3.1 本文相应的代码及资料已经以.ipynb文件和.pdf形式在github中给出。
-
.ipynb文件在链接/Coursera-deeplearning深度学习/课程1/week4/
-
.pdf文件在链接/Coursera-deeplearning深度学习
-
github地址:https://github.com/LSayhi/DeepLearning
点击【阅读原文】,github传送门了解一下。
我为什么喜欢你,那是因为从我出生以来,所有所见所闻都告诉我,你,最有趣,最美丽!
-by LSayhi的神经网络