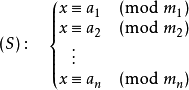数论选讲

一、容斥原理

1.什么是容斥原理

在计数时，必须注意没有重复，没有遗漏。为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理 ——度娘

2.公式

(1).一般形式

|A1⋃A2⋃…⋃An|=∑ni=1|Ai|−∑ni=1∑nj=i+1|Ai⋂Aj|+∑ni=1∑nj=i+1∑nk=j+1|Ai⋂Aj⋂Ak|−…
总结一下就是奇数个交就加上，偶数个交就减去。
下面附上两个图来帮大家理解一下

(2).对于数字的形式

这个与莫比乌斯反演有一定的关系，考虑到难度与时间的原因，这里先不做讲解，但是我可以剧透一下，这个只考虑没有重复质因子的数，然后分奇偶个质因子来考虑加减，一会在讲欧拉函数的时候会有涉及。

例题一：bzoj2839

二、扩展欧几里得算法

1.裴蜀定理

若a,b是整数,且（a,b）=d，那么对于任意的整数x,y,ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立。而扩展欧几里得算法就是用来求这样一组x,y。

2.算法原理

当b等于0的时候，a就是最后的gcd(a,b)，那么我们很容易构造出一组x,y即为x=1,y=0,也就是1*a+0*b==a，剩下的我们想办法通过这组解推出来。
设 ax1+ by1= gcd(a,b);
bx2+ (a mod b)y2= gcd(b,a mod b);
根据朴素的欧几里德原理有 gcd(a,b) = gcd(b,a mod b);
则:ax1+ by1= bx2+ (a mod b)y2;
即:ax1+ by1= bx2+ (a - [a / b] * b)y2=ay2+ bx2- [a / b] * by2;
也就是ax1+ by1 == ay2+ b(x2- [a / b] *y2);
根据恒等定理得：x1=y2; y1=x2- [a / b] *y2;

3.代码

根据上面的推导，我们不难得到这样的代码

int exGcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;y=0;
        return a;
    }
    int r=exGcd(b,a%b,x,y);
    int t=x;x=y;y=t-a/b*y;
    return r;
}

但是我们发现有x,y互换的过程，所以我们稍加改变，就可以得到一个更好看的写法

int exGcd(int a,int b,int& x,int& y)
{
    if(b==0)
    {
        x=1,y=0;
        return a;
    }
    int t=exGcd(b,a%b,y,x);
    y-=a/b*x;
    return t;
}

这个代码更加的好记，推荐背下来，虽然说不难推，但是考场上最好还是不要浪费时间在这个上QAQ，还有，千万别乱改这个代码，曾经你们的学姐把y-=a/b*x写成了x*a/b就错了2333。
现在我们得到的是一组可行的解，我们可以对这个解做出一些调整，现在我们的式子是 ax+by=(a,b) ，那么我们将x加b/(a,b)，将y减a/(a,b)等式显然依然成立，而且这样做可以得到所有的可行解。

三、欧拉函数

1.什么是欧拉函数

欧拉函数 Φ(n) 代表小于n并且与n互质的数的个数。

2.欧拉函数的求法

欧拉函数可以用如下方法求得
Φ(n)=n∗∏p|n且p为质数(1−1p)
这个公式怎么理解呢？
这是多个二项式乘起来的形式，也就是每项中我挑出来一个乘起来作为最后多项式的部分，那么我们如果这项选1则代表不选这项，选 −1p 就是选这一个数，而且选奇数个减，选偶数个加，这不就是容斥原理吗？我们用总集n减去是一个质因子倍数的数的个数加上是两个的减去是三个的，这也用到了数字容斥原理的一个特点：只考虑质因子幂次为1的数，因为幂次不是1的集合一定不是某几个集合的交，没有必要考虑。

3.欧拉函数的性质

(1).欧拉函数是积性函数(这个性质在一会讲线性筛的时候会做详细的解释)
(2).小于n与n互质的数的和为 Φ(n)∗n/2 (n=1的时候不满足此性质)
证明：如果a与p互质，那么p-a一定与p互质，则互质的数一定能两两组成一个p，证毕。
(3). n=∑p|nϕ(p)
证明：相当于枚举n的每一个因数，将n除以这个因数，和这个数互质的数的个数就是和n的gcd为这个因数的数的个数。

4.欧拉定理

当 (a,p)==1时  aΦ(p)≡1(mod p)

5.扩展欧拉定理

gcd(a,m)>1，且b>Φ(m)，ab≡a(b%Φ(m)+Φ(m))(mod m)
当 b<Φ(m) 时一般可以直接计算。

6.求欧拉函数的代码

long long phi(long long x)
{
    long long re=x;
    for(int i=2;i<=sqrt(x);i++)
    {
        if(x%i==0) re-=re/i;
        while(x%i==0) x/=i;
    }
    if(x!=1) re-=re/x;
    return re;
}

使用线性筛的话可以将求所有欧拉函数的时间优化到O(n),稍后再做讲解。

例题二：bzoj4173

四、逆元

1.什么是逆元？

逆元是在模意义下与 1a 等价的一个小于模数的整数，也就是说在模意义下除以一个数和乘以这个数是等价的。注意，只有当(a,p)==1的时候才有逆元存在，否则不存在逆元。

2.逆元的求法

(1).费马小定理

当p为质数时有 ap−1≡1(mod p)
我们将等式两边同时除以一个p得到 ap−2≡1a
所以当a,p互质的时候求a的逆元可以直接算 ap−2
优点：代码简单，只需一个快速幂
缺点：有局限性，p必须是质数

(2).欧拉定理

当 (a,p)==1时  aΦ(p)≡1(mod p)
由上面的费马小定理，我们不难想到，a的逆元即为 aΦ(p)−1
优点：没有局限性。
缺点：代码相对比较复杂。

(3).扩展欧几里得算法

由逆元的性质我们不难得到
a∗a−1≡1(mod p)
我们将这个式子转换一下，就得到了 a∗a−1+p∗y=1
我们发现这刚好是(a,p)==1并且求一组可行解使得 a∗x+p∗y==gcd(a,p)
所以我们用扩展欧几里得算法算一下x,y，最后的x就是a的逆元，再用上之前讲过的，x可以随意加上任意多个p，也就是对x在p意义下取一个模即可。
优点：无局限性，代码相对简单
缺点：思维复杂度较高（其实也没高到哪去，但是算是这三个里最难的了）

总结一下，推荐大家写的就是第一个和第三个，第二种算法我基本没见过人写QAQ

3.阶乘的求逆

首先阶乘求逆也要满足一个大框，就是这个阶乘要与模数互质。
阶乘的求逆有两种办法，一种是用O(n)的时间算出所有数的逆元，然后乘起来，但是这样难写，而且我也不会QAQ，我也没见过有人这么写，所以我给大家讲一个又简单有好写的算法。
我们先算出从1到n的阶乘，然后随便用上面的算法算一下 (n!)−1 ，然后我们用 (n!)−1 乘以一个n就得到了 ((n−1)!)−1 ，完事了，是不是简单多了。

五、BSGS

算法

讲了一大堆，我们来讲一个简单点的算法BSGS爽一爽，首先BSGS的全称是Baby Steps Giant Steps，也叫大步小步算法，名称即是算法的主要思想。
BSGS要求的东西是 满足ay≡x(mod p)的最小的一个y
和上面类似，BSGS算法也有一些前提要求，那就是a,p互质。
暴力的想法是枚举每一个y算一下等不等于x就行了，但是这显然太暴力了，是O(n)的，BSGS就是用来优化这个算法使其变成 O(n√) .
首先y最大的取值由欧拉定理可以得知小于 Φ(p) ，我们设这个值是m，我们设 t=m−−√ ，首先我们先将a的0次幂到t次幂算出来，放到桶里，然后枚举一个i，算 ai∗t ，然后对其求逆，用x乘以这个逆，若得到的数出现过，假设这个数是 ak 那么答案就是i*t+k.这样时间复杂度就是 O(n√) 的了。

代码

xy≡z (mod p) 求最小的一个y

        while(T--)
        {
            int x,z,p;
            scanf("%d%d%d",&x,&z,&p);
            x%=p;
            if(x==0 && z==0) 
            {
                printf("1\n");
                continue;
            }
            if(x==0) 
            {
                printf("Orz, I cannot find y!\n");
                continue;
            }
            pd.clear();
            mapp.clear();
            int kuai=sqrt(p);
            for(int i=kuai;i>=0;i--) 
            {
                int t=ksm(x,i); 
                mapp[t]=i;
                pd[t]=true;
            }           
            bool flag=false;
            for(int i=0;i*kuai<=p;i++) 
            {
                int t=ksm(x,i*kuai);
                t=1ll*ksm(t,p-2)*z%p;
                if(pd[t]) 
                {
                    printf("%d\n",i*kuai+mapp[t]);
                    flag=true;
                    break;
                }
            }
            if(!flag) printf("Orz, I cannot find y!\n");
        }

六、中国剩余定理（CRT）

引入

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？ ——《孙子算经》
相信这是在座各位都做过的小学奥数题，现在我们就来深入的研究一下这个问题的一般解法。

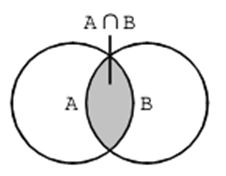
形式化

求出一组x使得所有同余方程成立。

解法

假设整数 m1,m2,…,mn 两两互质，则对任意的整数：a1,a2, … ,an，方程组有解，并且通解可以用如下方式构造得到：
设 M=∏ni=1mi,Mi=M∗m−1i,M−1i为Mi在mi意义下的逆元,则通解x=∑ni=1ai∗Mi∗M−1i

证明

既然是构造，我们只要证明这种构造方法满足上面的同余方程成立即可，我们考虑 x mod m1 的时候， M1∗M−11=1 ,则这一项等于a1，其余每一项的 Mi 都包含 m1 ，所以在 mod m1 的时候全部为0，所以 x≡a1(mod m1) ，其余每个方程同理，构造得证。

代码

long long china()
{
    long long t=0;
    for(int i=0;i<=3;i++)
    {
        long long mid=x[i]*Mi[i]%M;
        mid=mid*qiuni(Mi[i],modd[i])%M;
        t=(t+mid)%M;
    }
    return t;
}

七、组合数

1.前情提要

组合数在OI中的应用非常多，掌握组合数的求法非常重要。

2.组合数的求法

(1).阶乘法

组合数的阶乘公式： C(n,m)=n!m!(n−m)! ，在模数为质数且n<模数的时候我们可以使用上面的线性预处理阶乘和阶乘逆元的方法 O(n) 预处理， O(1) 求值。

int C(int n,int m)
{
    int re=1ll*jc[n]*njc[m]%P*njc[n-m]%P;
    return re;
}

(2).递推法

C(n,m)=C(n−1,m−1)+C(n−1,m) ，在n,m很小时，可以使用O(n*m)的递推法，对模数和n没有任何限制。初始值C(i,0)=1.

for(int i=0;i<=n;i++) C[i][0]=1;
for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
        C[i][j]=(C[i-1][j-1]+C[i-1][j])%p;

(3).lucas定理

当n>p并且p为质数的时候，我们可以使用lucas定理
C(n,m)=C(n/p,m/p)*C(n%p,m%p)%p
这样将n,m缩小到小于p就可以使用第一种阶乘求组合数的办法了。

int lucas(int n,int m)
{
    if(n<m) return 0;
    if(n>=P || m>=P) return 1ll*lucas(n%P,m%P)*lucas(n/P,m/P)%P;
    return C(n,m);
}

(4).CRT+lucas

当p不是质数，但是p的所有质因子的幂次都为1的时候，我们可以将p分解成若干个质因子的乘积，分别对每一个质因子用lucas定理求解，最后将所有答案用CRT合并。

(5).万能的算法

此算法对p和n没有任何限制，类似于阶乘的算法，我们先将p分解质因数，然后在算阶乘的时候乘每一个数的时候都将这个数的所有p的质因子除干净并记录一下到n为止p的所有质因子都有多少个，这样最后求出来的n!一定与p互质，就可以用扩展欧几里得求一下逆元，用之前的办法，求出所有n!的逆元，再乘上每一个p的质因子的多少次方就可以了。

void shai()
{
    tt=0;
    int t=mod;
    for(int i=2;i*i<=mod && t!=1;i++)
    {
        if(t%i==0)
        {
            P[++tt]=i;
            while(t%i==0) t/=i;
        }
    }
    if(t!=1) P[++tt]=t;
    jc[0]=njc[0]=1;
    for(int i=1;i<=n+m;i++)
    {
        int x=i;
        memcpy(Pow[i],Pow[i-1],sizeof(Pow[i]));
        for(int j=1;j<=tt;j++)
            while(x%P[j]==0) x/=P[j],Pow[i][j]++;
        jc[i]=1ll*jc[i-1]*x%mod;
        njc[i]=get_inv(jc[i]);
    }   
}
int C(int n,int m)
{
    if(n<m) return 0;
    int re=1ll*jc[n]*njc[n-m]%mod*njc[m]%mod;
    for(int i=1;i<=tt;i++) re=1ll*re*ksm(P[i],Pow[n][i]-Pow[m][i]-Pow[n-m][i])%mod;
    return re;
}

还有很多很多算法，但是我觉得这些就够用了。
总之，对于不同的n与p还有求组合数的次数，我们有很多不同的办法，每个算法都有一定的局限，要随机应变。

例题三：bzoj1951

八、线性筛

1.前言

线性筛，顾名思义就是在线性时间内筛出我们想要的东西的算法，它能线性筛出质数、欧拉函数、莫比乌斯函数还有一些奇怪的积性函数。

2.线性筛素数讲解

我们先放上代码

    for(int i=2;i<=N;i++)
    {
        if(!pd[i]) pri[++top]=i;
        for(int j=1;i*pri[j]<=N;j++)
        {
            pd[i*pri[j]]=true;
            if(i%pri[j]==0) break;
        }
    }

为什么i%pri[j]==0时要break呢，又为什么这份代码是O(n)的呢？
我们考虑i*pri[j]，如果i是一个合数，那么i一定可以拆分乘一个质数乘上一个别的数，如果这个质数比pri[j]要小的话那么一定用这个质数就可以筛掉这个数，而不用pri[j]，而我们遍历的是每一个质数，也就是说我们一定会在一个时候枚举到i最小的一个质因子，再往大了的质因子都不应该用i消去，所以在这个时候跳出即可，而每一个数一定只会被它最小的质因子筛掉，所以总时间复杂度是O(n)的。

3.线性筛一些其他的函数

(1).欧拉函数

首先根据积性函数的性质，如果i,j互质，则 f(i∗j)=f(i)∗f(j) .
所以对于 i%pri[j]!=0 的情况，phi[i*pri[j]]直接等于phi[i]*phi[pri[j]]即可。
对于 i%pri[j]==0 的情况，考虑求解phi的公式，多乘一个pri[j]并不会多一个质因子，只有前面的n多乘了一个pri[j]，所以这种情况phi[i*pri[j]]=phi[i]*pri[j]

    phi[1]=1;
    for(int i=2;i<=N;i++)
    {
        if(!pd[i])
        {
            pri[++top]=i;
            phi[i]=i-1;
        }
        for(int j=1;i*pri[j]<=N;j++)
        {
            pd[i*pri[j]]=true;
            if(i%pri[j]==0)
            {
                phi[i*pri[j]]=phi[i]*pri[j];
                break;
            }
            phi[i*pri[j]]=phi[i]*(pri[j]-1);
        }
    }

(2).莫比乌斯函数以及其他积性函数

不是这里要讲的重点，如果有时间再细说，先放上莫比乌斯函数的代码

    u[1]=1;
    for(int i=2;iif(!pd[i])
        {
            zs[++top]=i,
            u[i]=-1;
        }
        for(int j=1;zs[j]*i*i]=true;
            if(i%zs[j]==0) break;
            u[i*zs[j]]=-u[i];
        }
    }

结语

这篇博客讲解的数论知识相对比较简单，但已经涵盖了OI中数论的大部分知识，数论很有趣，希望大家爱上数论2333