MIT线性代数习题全解

习题集1

第一题

这里实际上用到了这个等式:
cos(β−α)=cos(β)cos(α)+sin(β)sin(α) cos ⁡ ( β − α ) = cos ⁡ ( β ) cos ⁡ ( α ) + sin ⁡ ( β ) sin ⁡ ( α )

第二题

三个向量，两两夹角大于90度

第三题

x1,x2,x3为w1,w2,w3线性组合的系数，向量之间的线性组合为零向量即为向量相互依赖的定义。由于3个向量不独立，因此在3维空间中形成了一个2维的超平面

第四题

可以看出C中第一行和第五行的组合可以形成第三行，因此只会有4个向量来构成平面，即在5维空间中的四维超平面。

第五题

总量不变为马尔科夫变换的性质。可以想象为两地之间的人口迁徙，无论怎么迁徙，人口总数是不变的。

第六题

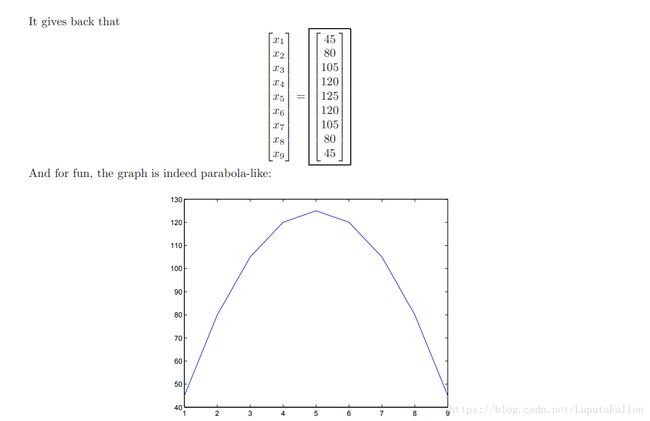
如下为这题的python代码:

from numpy import *
import matplotlib
import matplotlib.pyplot as plt

u = mat([[1, 0]]).transpose()
A = mat([[.8, .3], [.2, .7]])
k = [i for i in range(7)]
res = []
for i in range(7):
    u = A * u
    res.append((u.A[0][0], u.A[1][0]))

fig, ax = plt.subplots()
ax.plot(k, res)
plt.show()
u = mat([[0, 1]]).transpose()
res = []
for i in range(7):
    u = A * u
    res.append((u.A[0][0], u.A[1][0]))

ax.plot(k, res)
plt.show()

第七题

如果行向量或者列向量不独立，则矩阵奇异。不独立的定义就是线性组合为0向量。通过第一行和第二行的线性组合构造第三行，调整b值，使其不满足等式

第八题

很简单的奇异矩阵的性质问题。

第九题

E为消元法中用到的行转换矩阵，例如:
E21=⎡⎣⎢1−10010001⎤⎦⎥ E 21 = [ 1 0 0 − 1 1 0 0 0 1 ] 表示一个第二行减去第一行的转换

第十题

考察行转换矩阵E的一题。其中通过多次E的转换到I的过程实际就是消元法的过程

第十一题

第十二题

第十三题

主要考察的是，row1 + row 2 = row3 -> b1 + b2 = b3

习题集2

第一题

通过Gauss-Jordan得出逆矩阵，公式为 UI−>IU−1 U I − > I U − 1

第二题

第三题

我们可以得到
E=⎡⎣⎢⎢⎢1−1−1−101−1−1001−10001⎤⎦⎥⎥⎥ E = [ 1 0 0 0 − 1 1 0 0 − 1 − 1 1 0 − 1 − 1 − 1 1 ] 将E除对角线以外元素乘以-1即可得到L，因为L相当于把U还原成A的矩阵。

第四题

第五题

第六题

第七题

第八题

第九题

标准正交矩阵Q的几个性质

第十题

子空间的定义:在子空间中任意向量的线性组合仍在子空间中

第十一题

如果b为列向量的线性组合，即在列空间中，则增加b不会增加列空间，而这也正对应了Ax = b有解，因为Ax = b有解的条件就是b在列空间中

第十二题

第十三题

习题集3

第一题

第二题

由列向量可以得出m = 3,由零空间向量可以得出n = 3

第三题

第四题

有4个节点，由于它们的入度与初度之和等于0，可以得到4个等式，构造 Ax=0 A x = 0 ,通过消元法确定主元和自由变量，得到零空间的解

第五题

第六题

第七题

需要注意的一点是，行转换不会改变零空间

第八题

第九题

第十题

第十一题

第十二题

第十三题

第十四题

习题集4

第一题

第二题

需要注意的是，行空间与零空间垂直，因此第三问直接选第一行就可以

第三题

第四题

这题有个小错误.
P21P32=⎡⎣⎢010001100⎤⎦⎥ P 21 P 32 = [ 0 0 1 1 0 0 0 1 0 ]

第五题

四个子空间的关系，行空间，列空间为r维，零空间和转置零空间为n - r维，m - r维

第六题

第七题

第八题

第九题

第十题

习题集5

第一题

第二题

第三题

第四题

第五题

第六题

第七题

第八题

注意,P投影到列空间， I−P I − P 投影到左零空间

第九题

第十题

第十一题

第十二题

第十三题

习题集6

第一题

第二题

第三题

第四题

第五题

第六题

第七题

第八题

第九题

第十题

注意，若矩阵奇异，则行列式为0,。

第十一题

对行进行操作不会改变行列式的值

第十二题

第十三题

习题集7

第一题

将三对角线矩阵的行列式按cofacors展开，可以发现满足斐波拉契数列的性质

第二题

第三题

第四题

注意, ACT A C T 为 detAI d e t A I

第五题

第六题

第七题

第八题

第九题

第十题

第十一题

注意，这里求 S−1 S − 1 有点小技巧,行列式的倒数乘以cofactors矩阵的转置

第十二题

第十三题

习题集8

第一题

注意，转换用到了泰勒展开

第二题

第三题

第四题

第五题

第六题

第七题

第八题

第九题

对称矩阵，特征值为实数

第十题

第十一题

第十二题

第十三题

习题地址为:
https://ocw.mit.edu/courses/mathematics/18-06-linear-algebra-spring-2010/assignments/
有空的话建议还是去看看~
持续更新~