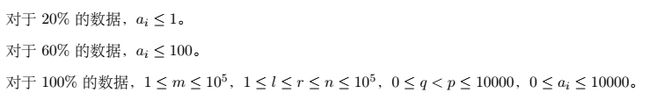同余【NOIP2016提高A组模拟9.2】

题目

样例输入：

5 2
1 5 2 3 7
1 3 2 1
2 5 3 0

样例输出：

2
1

---

剖解题目

……

---

思路

一开始是想到开100000个树状数组存储，然后就看到了空间爆炸。之后就想到了莫队，不过虽然听说过，但没有了解过莫队算法，就一脸懵逼了。
其实也不需要用莫队。

---

解法

20%：ai<=1，所以转化位求区间0与1的个数，前缀和优化。注意p=1时。时间O(n+m).
60%：同上，开101个前缀和。时间O(ai(n+m))
100%：我们离线处理，把每一个询问拆成求1~r-1~l-1，然后就可以从开始一条扫描线。
我们用个桶记录每个数出现的次数，那么对于当前的p,q，只需要查找桶中下标是k* p+q的就可以了，k的范围是从0开始，直到k *p+q>max(a[i])。
但如果当p很小的时候，k就要循环很多次才会达到退出条件，这样会爆炸。
我们可以分两端处理，寻找一个M，当p>M时就进行上述处理，否则便进行下述处理。
因为此时p很小，我们可以设g[i][j]表示模i后值为j的数的个数，在计算时直接扔进答案即可。
那么时间 O(nM+m∗ai/M) ,当M=sqrt(ai)=100时，时间最少。

---

代码

#include
#include
#include
#define fo(i,a,b) for(int i=a;i<=b;i++)

using namespace std;

const int maxn=1e5+1,maxm=101;
int t[maxn],g[maxm][maxm],ans[maxn][2],a[maxn];
int n,m,tot,num,maxx;
struct cy{
    int x,p,q,bz,num;
}b[maxn*2];
bool cmp(cy a,cy b)
{
    return a.xx;
}
int main()
{
    //freopen("T.in","r",stdin);
    scanf("%d%d",&n,&m);
    fo(i,1,n) {
        scanf("%d",&a[i]);
        maxx=max(maxx,a[i]);
    }
    fo(i,1,m){
        int l,r,p,q;
        scanf("%d%d%d%d",&l,&r,&p,&q);
        b[++tot].x=l-1;
        b[tot].p=p;
        b[tot].q=q;
        b[tot].bz=1;
        b[tot].num=i;
        b[++tot].x=r;
        b[tot].p=p;
        b[tot].q=q;
        b[tot].bz=2;
        b[tot].num=i;
    }
    sort(b+1,b+tot+1,cmp);
    int ii=0;
    fo(i,1,tot){
        while (iix) {
            ++ii;
            t[a[ii]]++;
            fo(j,1,100) g[j][a[ii]%j]++;
        }
        if (b[i].p<=100) ans[b[i].num][b[i].bz-1]=g[b[i].p][b[i].q];
        else {
            fo(k,0,100) {
                if (k*b[i].p+b[i].q>maxx) break;
                ans[b[i].num][b[i].bz-1]+=t[k*b[i].p+b[i].q];
            }
        }
    }
    fo(i,1,m) printf("%d\n",ans[i][1]-ans[i][0]);
}