北航OJ-2014级第1次算法上机题解

北航OJ-2014级第1次算法上机题解

---

A. 零崎的人间冒险Ⅰ

题目描述

　　零崎最近一段时间非常无聊，于是他决定进行一场冒险，然而无聊的人遇到的冒险也非常的无聊，他的冒险刚刚开始就要结束了。理由也非常的无聊，因为一个无聊的大魔王决定用一个非常有魔(wu)力(liao)的方式毁灭世界。
　　魔王有三个具有魔(wu)力(liao)的杆，暂时称为ABC，还有n个具有魔(wu)力(liao)的大小全都不同的盘子，这些盘子按照大小顺序放在A杆上，现在魔王要用具有魔(wu)力(liao)的方式移动到C杆，移动的过程中，小的盘子仍然只能摆在大的盘子上面而不能发生错乱，否侧魔王的魔法就会失灵。 然而魔王似乎想找一个无聊的人来替他完成这个魔法，而无聊的零崎也觉得这个事情非常的无聊，干脆就决定还是让你们去做。
　　 零崎也不知道这个无聊的魔王到底有多少个有魔(wu)力(liao)的盘子，所以他说多少个你们就当是多少个吧。

输入

多组数据，每组一个数字n表示魔王的盘子数。

输出

对于每组数据，输出为魔王魔法发动后盘子移动的过程，两组输出之间用空行隔开。

输入样例

1
2

输出样例

A to C

A to B
A to C
B to C

解题思路：

这道题考查递归。
由于数据结构上机中已经遇到多次，所以这里只是简单回顾汉诺塔递归算法的整体思路：

Case 1：当A塔上只有一个盘子时，只需要将 A塔上的一个盘子移到 C塔上。
Case 2：当A塔上有n个盘子时（n>1），先将A塔上编号1至n-1的盘子（共n-1个）移动到B塔上（借助C塔），然后将A塔上最大的n号盘子移动到C塔上，最后将B塔上的n-1个盘子移动到C塔上。

解题代码

#include 

//hanoi函数的功能：将 n 个盘子从 A 移到 C 的过程展示出来，柱子 B 起到辅助移动的作用
void hanoi(int n, char A, char B, char C)
{
    if(n == 1)
        printf("%c to %c\n", A, C);
    else
    {
        hanoi(n-1, A, C, B);
        printf("%c to %c\n", A, C);
        hanoi(n-1, B, A, C);
    }
}

int main()
{
    int n;
    while(scanf("%d", &n) != EOF)
    {
        hanoi(n, 'A', 'B', 'C');
        printf("\n");
    }
}

---

B. 零崎的人间冒险Ⅱ

题目描述

　　零崎本以为他的无聊冒险马上就要结束了，然而实际上距离魔王的魔法成功发动还有很久很久，于是他的无聊冒险还可以继续……
　　无聊的零崎需要给自己的冒险找点事做，然而实际上他的日常非常平和，如果说有什么意外的话，那就是他去打麻将了。
　　零崎在玩一种叫做日式麻将的竞技游戏，然而无聊的零崎总是遭遇别人立直需要防守的场面。零崎在防守时，会跟打现物和搏筋兜牌两种技能，然而为了不被婊得太惨，零崎不会连续搏筋兜牌。也就是说，零崎任意两次选择中不会都是搏筋兜牌。
　　那么对于n次舍牌，无聊的零崎会有多少种选择？
　　因为无聊的零崎可以打很久的麻将，所以n可能很大，无聊的零崎决定只要结果对100007求模后的选择数。

输入

多组输入数据，每组一个数字n，1<=n<=Int_MAX

输出

每组一行，只需要选择种数对100007求模后的结果。

输入样例

1
2

输出样例

2
3

解题思路

Part 1 递推公式的推导　　

　　 我们用O和X分别表示现物和搏筋兜牌。
　　假设有3次舍牌，我们可以很容易地枚举出所有排列方式：OOO, OOX, OXO, XOO, XOX，我们把每一个这样的一个序列叫做一种舍牌方式。

　　为了方便讨论，我们给出如下定义：

F(n) = n次舍牌中不同的舍牌方式数

　　比如上面的例子中，F(3) = 5。

　　我们来尝试推导具有普适性的公式：
　　假设F(n-2)种舍牌方式中，有m次以现物结束（类似于OXOXXX……O），F(n-2) - m次以搏筋兜牌结束（类似于OXOXXX……X）。
　　对于类似OXOXXX……O的舍牌方式，下一次舍牌既可以是O也可以是X，所以下一次有2*m中舍牌方式；对于类似OXOXXX……X的舍牌方式，下一次只能是O，所以下一次舍牌有F(n-2) - m种方式。
　　我们把两种舍牌方式数相加，就得到：

F(n-1) = 2*m + F(n-2) - m = F(n-2) + m
　　同理，由上面的推理结论，F(n-1)中有F(n-2)次以O结束，m次以X结束，所以：

F(n) = 2*F(n-2) + m = (F(n-2) + m) + F(n-2) = F(n-1) + F(n-2)
　　而这就是斐波那契数列的递推公式。

Part 2 取模运算的处理技巧

　　题目中要对其进行取模处理。这里需要补充一个结论：

斐波那契数列对某个整数取模的结果构成循环数列
　　这个结论的证明很繁琐，故不在此列出，可以去这篇博文下查看： http://blog.csdn.net/ACdreamers/article/details/25616461
　　由于时间和空间有限，不可能使用递归方法对于每一个输入值进行求解。故进行预处理操作，把一个周期内的斐波那契数取模后的结果存入数组。对于之后的每一次查询，只需要用循环周期对其进行取模操作，然后根据余数直接读取数组里保存的值。

解题代码

#include 
#define INF 0xFFFFFF
using namespace std;
int remainders[100000];//取余后的斐波那契数列，仅保存一个周期的数
int T = 2;//循环节

void calFibonacciRemainders()
{
    remainders[0] = 1;
    remainders[1] = 2;
    while (1)
    {
        remainders[T] = (remainders[T - 1] + remainders[T - 2]) % 100007;
        if (remainders[T] == remainders[1])
        {
            T--;
            break;
        }
        T++;
    }
}

int main()
{
    calFibonacciRemainders();
    int n;
    while (cin >> n)
    {
        n %= T;
        if (n == 0)
            n = T;
        cout << remainders[n] << endl;
    }
}

---

C. Let’s play a game

题目描述

这是一个古老而无聊的游戏，这是一个欧几里得躺枪的游戏。Nova君和LaoWang决定一分胜负。给定两个正整数a,b。Nova君和LaoWang轮流从中将较大的数字减去较小数字的整数倍（1倍，2倍等等）。并且保证每次减完不会出现负数的情况。由Nova君先手。最终在自己回合将其中一个数变为0的一放获胜。两个人智商都还行，都会采取最优策略，谁会赢呢？

输入

多组测试数据。对于每组测试数据，给出两个数字a和b（保证Int范围内）

输出

对于每组数据，输出获胜者的名字。

输入样例

34 12
15 24

输出样例

Nova
LaoWang

解题思路

Part 1 问题分析

　　 博弈论的游戏总有“宿命”的意味，即游戏结果早已被初始设定的条件所决定，游戏过程的种种局势不外以下二者中的一个：

    1.必胜态：在此状态行动的玩家必胜
    2.必败态：在此状态行动的玩家必败

　　判断方法如下：
　　 1. 若一个状态可转移到必败态，则此状态为必胜态。（即如果我的一种策略能让对手进入必败态，我肯定采取这个策略，故我肯定获胜，故这是个必胜态。这也就是“智商都还行”的意思）
　　 2. 若一个状态只能转移到必胜态，则此状态是必败态。（无论我怎么挣扎对手都必胜，则我必败）
　　所以如果我们对于每种局势，枚举出所有的情况和结局，就能够判断出当前状态是必胜态还是必败态。

Part 2 递归思路

　　 所以这题的问题转化成：如何进行枚举？这里我们使用递归解决。
　　对于两个数字bigNum和smallNum（假设bigNum>＝smallNum），构造一个递归判断函数 judge(int bigNum, int smallNum)，它可以判断出拿到这两个数字的人是输还是赢。

递归方法如下：
(1) smallNum == 0
　　这说明拿到这个数的人输了，因为上一个人把两个数中的一个减成了0，所以这时返回lose。
(2) smallNum != 0
　　这说明这个局势可能是必胜态，也可能是必败态。我们需要对所有的可能进行枚举并判断，才能下结论。对于所有的操作方案： bigNum – smallNum, bigNum – 2*smallNum, … , bigNum - floor(bigNum/smallNum) * smallNum，这些方案会产生不同的结果，可能产生必胜态，也可能产生必败态。只要结果中有必败态，这个人就可以通过让对方进入这个必败态来获胜，故当前的局势是一个必胜态；但如果所有操作方案的结果都不是必败态，那么当前就是一个必败态！
　　所以我们只需要对于上面列举的所有操作方案，再次使用judge函数，判断结果中有没有必败态，就可以知道当前的状态是必胜态还是必败态！当递归调用从底层向上返回结果至第一次递归调用（即初始状态）时，我们就能知道初始状态是必胜态还是必败态！

解题代码

#include 
const bool lose = false;
const bool win = true;

bool judge(int a, int b)
{
    if (a < b)
    {
        a = a^b;
        b = a^b;
        a = a^b;
    }
    if (b == 0)   //说明上一个人已经把b变成了0，所以上一个人赢了，这个人输了。
        return lose;
    for (int i = a / b; i > 0; i--)      //最多能够从a里面减去a/b个b（保证非负）
        if (judge(a - b*i, b) == lose)     //判断下一个人是否会成功
            return win;
    return lose;
}

int main()
{
    int x, y;
    while (scanf("%d%d", &x, &y) != EOF)
        printf("%s\n", judge(x, y) ? "Nova" : "LaoWang");
}

---

D. 零崎的人间冒险Ⅲ

题目描述

　　不打麻将的零崎特别的无聊，所以他又四处乱逛了。
　　四处乱逛的无聊零崎遇到了另一个特别无聊的人，因为这个人竟然在无聊的算各种一元n次多项式a0+a1x+a2x^2+……+anx^n！这个无聊的人算的实在太慢了令零崎忍不住想开启嘲讽模式，所以现在，快来给零崎搞一个能快速计算多项式的东西吧。（其实可能也不用特别快）

输入

多组输入数据。 每组数据以多项式次数n开始，下一个数字为变量x，之后n+1个数字为系数a0……an。输入数据保证在int范围内

输出

每行一个结果，也许n特别大所以最后结果还是对1e6+7求模吧……

输入样例

1 2 1 2  
3 2 1 2 3 4

输出样例

5
49

解题思路

两种思路：
(1) 分别求每一项，然后加（TLE妥妥的）；
(2) 霍纳法则： a0+a1x+a2x^2+……+anx^n = a0+x*(a1+x*(a2+…x*(an-1 + x*an)…))，然后写个for循环从内往外求 （完美AC）。

解题代码：

#include 
int A[1000000];
int div = 1000007;
int main()
{
    int n, x, sum;
    while (scanf("%d%d", &n, &x) != EOF)
    {
        for (int i = 0; i <= n; i++)
            scanf("%d", &A[i]);
        sum = 0;
        for (int i = n; i > 0; i--)
            sum = (sum + A[i])*x%div;
        printf("%d\n", (sum + A[0]) % div);
    }
}

---

E. Inverse number：Reborn

题目描述

输入一个正整数n，随后给出一个长度为n的整数序列a1,a2,a3…an。求给定序列的逆序数。
概念回顾：
逆序对：数列a[1],a[2],a[3]…中的任意两个数a[i],a[j]，如果a[i]>a[j],那么我们就说这两个数构成了一个逆序对。
逆序数：一个数列中逆序对的总数。

输入

多组测试数据。对于每组测试数据，给出序列长度 n 和一个长度为 n 的序列a1,a2,a3...an (0<n<=10^6，保证ai在int范围内)

输出

对于每组数据，输出该序列的逆序数。

输入样例

7 
3 5 4 8 2 6 9

输出样例

6

Hint

1、用n^2的算法是不行不行滴╮(╯_╰)╭
2、分治法

解题思路

一开始用了最简单的分治法，然而一直TLE。代码如下：

#include 
int A[1000000];
long long B[1000000];
int main()
{
    long long n, reverseNumber, temp;
    while (scanf("%lld", &n) != EOF)
    {
        scanf("%d", &A[0]);
        B[0] = 0;
        for (int i = 1; i < n; i++)
        {
            reverseNumber = 0;
            scanf("%d", &temp);
            A[i] = temp;
            for (int j = 0; jif (A[j] > temp)
                    reverseNumber++;
            B[i] = B[i - 1] + reverseNumber;
        }
        printf("%lld\n", B[n - 1]);
    }
}

　　这题是用如下思想做的：由于升序排列的数组逆序数为０，所以现有数组的逆序数＝把现有数组变成升序排列的数组的过程中所改变的逆序数！
　　我们使用归并排序实现上述思想（用归并排序的原因下面会讲，而以下内容的展开建立在你理解了归并算法的基础上）

　　先定义两个概念：
　　leftSubArray（左子数组）：归并排序中位于分割点左侧的子数组
　　rightSubArray（右子数组）：归并排序中位于分割点左侧的子数组

　　归并排序的Merge操作把leftSubArray和rightSubArray合并成一个数组，也就是在这个过程中发生了逆序数的改变。

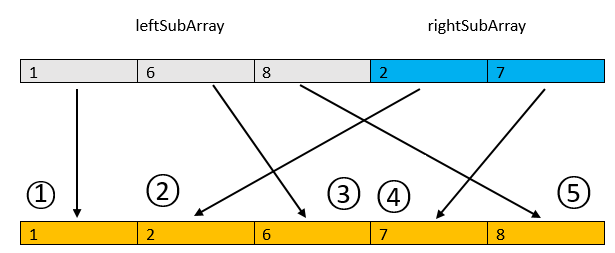
　　 现在我们以上图的Merge操作为例，分析一下逆序数是如何改变的：
　　 首先，由于leftSubArray本身按升序排列好，逆序数为0，所以对于leftSubArray自身的元素而言，原来在左边1，绝对不会被插入到2,6右边，也就是说插入操作不造成1,2,6之间的相对位置交换，自然也就不改变1,2,6之间的顺序关系（对于rightSubArray也同理）。所以逆序数改变的原因必定是leftSubArray和rightSubArray之间的元素顺序的交换！
　　假设我们现在把一个来自leftSubArray中的元素L插到新的数组里，如果在它之前，已经有一些rightSubArray的数字插入新数组了（比如上图中rightSubArray中的数字2在leftSubArray中的6之前被插入到新数组中），说明原来在L右边的数被移到了L左边，这些数字的个数就是逆序数的改变值；等价地，我们还可以这样看：将rightSubArray中的元素R插入新数组时，如果leftSubArray中还有一些元素没有插入，那么它们就只能被插入到R后面了（比如上图中插入2后，leftSubArray里的6和8就只能被插到2后面了），这些元素的数目就是逆序数的改变值。所以我们只需要选择其中一个角度作为标准，就可统计出排序改变的逆序数，即原数组的总逆序数。
　　为什么用归并排序？用快排不行么？可以，但是统计逆序数改变值时，快排得进行元素间的一一比较，特别费时，而归并排序可以直接算出改变的逆序数，我们使用如下实例讲解：

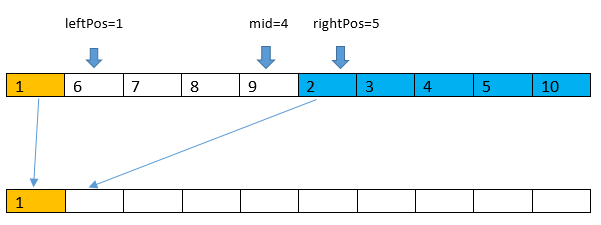
现在1已经归位，我们把2插入新数组的过程中，2跨过了leftSubArray中6,7,8,9这4个元素。由于Merge函数里记录了leftPos，rightPos，mid变量，所以可以直接用　mid-leftPos+1=4　 算得逆序数。

解题代码

#include 
#define INF 0xFFFFF
long long A[1000000];
long long number;

void Merge(int left, int mid, int right)
{
    int len1= mid - left +1;
    int len2 = right - mid;
    int L[len1+ 1], R[len2 +1];
    for(int i =0; ileft +i];
    for(int i = 0; imid+i+1];
    L[len1] =R[len2] =INF;
    int l = 0, r= 0;
    for(int i = left; i<= right; i++)
    {
        if(L[l] <= R[r])
            A[i] = L[l++];
        else
        {
            A[i] = R[r++];
            number += len1 - l;
        }
    }
}

void mergeSort(int left, int right)
{
    if(left<right)
    {
        int mid = (left + right)/2;
        mergeSort(left, mid);
        mergeSort(mid +1, right);
        Merge(left , mid, right);
    }
}

int main()
{
    long long n;
    while(scanf("%lld", &n)!=EOF)
    {
        number = 0;
        for(int i = 0; i"%lld", &A[i]);
        mergeSort(0, n-1);
        printf("%lld\n", number);
    }
}

---

F. 零崎的人间冒险Ⅳ

题目描述

　　在干掉了guangtou之后，无聊的零崎又去找事了……
　　说起来零崎前几周学到了一个叫做Apriori算法的东西，其第一步是挑出所有出现频率大于某个给定值的数据。然而作为一个具有一定程度的强(qiǎng)迫(pò)症的人，零崎显然希望先排个序再对其子集进行操作。 于是，现在的任务是简单的升序排列。

输入

多组输入数据，每组两行，第一行为一个整数n。第二行为n个整数。

输出

每组一行，输出n个整数的升序排列，两个整数之间用一个空格隔开。

输入样例

5
6 5 2 3 1 

输出样例

1 2 3 5 6

解题思路

基础的排序题目。
使用快速排序就可以AC了。
简单复习一下快排思想：
1．先从数列中取出一个数作为基准数。
2．分区，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
3．再对左右区间重复第二步，直到各区间只有一个数。

解题代码

#include 
using namespace std;

void quickSort(int A[], int left, int right)
{
    if (left < right)
    {
        int l = left, r = right;
        int temp = A[left];
        while (l < r)
        {
            while (l < r && A[r] >= A[l]) //一定记住要加等于号，在下面加也行
                r--;
            swap(A[l], A[r]);
            while (l < r && A[l] < A[r]) //在这里加等于号也行，但两个地方必须有一个加等号
                l++;
            swap(A[l], A[r]);
        }
        A[l] = temp;
        quickSort(A, left, l - 1);
        quickSort(A, l + 1, right);
    }
}

int main()
{
    int len, A[100000];
    while (cin >> len)
    {
        for (int i = 0; i < len; i++)
            cin >> A[i];
        quickSort(A, 0, len - 1);
        for (int i = 0; i < len; i++)
            cout << A[i] << " ";
        cout << endl;
    }
}