线性代数及其应用:第三章 正交
文章目录
- 第三章 正交
- 1. 正交向量与子空间
- 1.1. 内积
- 1.2. 矩阵四大子空间的正交关系
- 1.3. 矩阵的真正作用
- 2. 向量投影到向量
- 3. 向量投影到列空间与最小二乘法
- 3.1. 向量投影到列空间
- 3.2. 最小二乘法问题
- 3.2.1. 代数法
- 3.2.2. 矩阵法
- 4. 正交基,Gram-Schmidt正交化法
- 4.1. 正交基
- 4.1.1. 正交矩阵
- 4.1.2. 正交变换
- 4.1.3. 正交矩阵列空间的正交基
- 4.2. Schmidt正交化法(施密特正交化法)
- 4.3. 矩阵的正交分解
- 4.4. Hilbert空间
- 5. 应用:快速傅里叶变换(FFT)
- 5.1. 傅里叶级数
- 5.2. 离散傅里叶变换
- 5.3. 快速傅里叶变换
前言:这篇blog是《 Linear Algebra and Its Applications》第三章的一些学习笔记
第三章 正交
这一章引出新工具:内积,投影
重点:施密特正交化法
1. 正交向量与子空间
1.1. 内积
向量 α , β \alpha,\beta α,β的内积定义成 < α , β > = α T β <\alpha,\beta>=\alpha^{T}\beta <α,β>=αTβ,可以理解成 R n × R n → R R^{n}\times R^{n}\rightarrow R Rn×Rn→R的映射,向量模的平方就是自己与自己的内积 ∣ ∣ x ∣ ∣ 2 = x T x ||x||^{2}=x^{T}x ∣∣x∣∣2=xTx。内积有如下性质:
- < α , α > ≥ 0 <\alpha,\alpha> \geq 0 <α,α>≥0
- < α , β > = < β , α > <\alpha,\beta>=<\beta,\alpha> <α,β>=<β,α>
- < α + γ , β > = < α , β > + < γ , β > <\alpha+\gamma,\beta>=<\alpha,\beta>+<\gamma,\beta> <α+γ,β>=<α,β>+<γ,β>
- < c α , β > = c < α , β > <c\alpha,\beta>=c<\alpha,\beta> <cα,β>=c<α,β>
1.2. 矩阵四大子空间的正交关系
在 R n R^{n} Rn空间,行空间与零空间正交互补,记为 C ( A T ) = ( N ( A ) ) ⊥ C(A^{T})=(N(A))^{\bot} C(AT)=(N(A))⊥,即 d i m ( N ( A ) ) + d i m ( C ( A T ) ) = n dim(N(A))+dim(C(A^{T}))=n dim(N(A))+dim(C(AT))=n, d i m ( ) dim() dim()表示向量空间的维度。
在 R m R^{m} Rm空间,列空间与左零空间正交互补,记为 C ( A ) = ( N ( A T ) ) ⊥ C(A)=(N(A^{T}))^{\bot} C(A)=(N(AT))⊥,即 d i m ( N ( A T ) ) + d i m ( C ( A ) ) = m dim(N(A^{T}))+dim(C(A))=m dim(N(AT))+dim(C(A))=m, d i m ( ) dim() dim()表示向量空间的维度。
列空间与左零空间正交互补,即两者列空间与左零空间的向量相加,可以构成 R m R^{m} Rm,正交互补并不是说 R m R^{m} Rm中只有列空间与左零空间,列空间和左零空间的向量也是有m个数组成的,在 r < m r<m r<m时, R m R^{m} Rm相对于 C ( A ) C(A) C(A)与 N ( A T ) N(A^{T}) N(AT)是更高维,一个高维空间,不能由两个低维空间构成,但可以说, R m R^{m} Rm向量空间中的一个向量 x x x,可以由 C ( A ) C(A) C(A)的一个向量 x 1 x_{1} x1与 N ( A T ) N(A^{T}) N(AT)一个向量 x 2 x_{2} x2相加构成,关于这一点可以类比三维直角坐标系,三维任一点可以由xy平面一点的坐标和z直线上一点的坐标相加得到,但并不能说三维平面只有xy平面和z直线;在 r = m r=m r=m时, R m = C ( A ) , N ( A T ) = ∅ R^{m}=C(A), N(A^{T})=\varnothing Rm=C(A),N(AT)=∅。
如何证明正交补?主要还是因为 d i m ( N ( A T ) ) + d i m ( C ( A ) ) = m dim(N(A^{T}))+dim(C(A))=m dim(N(AT))+dim(C(A))=m,且 N ( A T ) N(A^{T}) N(AT)中向量和 C ( A ) C(A) C(A)中向量正交。
1.3. 矩阵的真正作用

如上图所以,左边的两个矩形空间是行空间(row space,维度为r)与零空间(nullspace,维度为n-r);右边的两个矩形空间是列空间(column space,维度为r)与左零空间(left nullspace,维度为m-r)。同时矩形空间之间的" └ \llcorner └"符号表示了两个子空间之间是正交的。
从 R n R^{n} Rn中找一点x,可表示为 x = x r + x n x=x_{r}+x_{n} x=xr+xn, x r x_{r} xr表示行空间中的某一向量, x n x_{n} xn表示零空间中的某一向量,而矩阵 A m × n A_{m\times n} Am×n作用于 x x x,即 A x = A ( x r + x n ) = A x r + 0 = b Ax=A(x_{r}+x_{n})=Ax_{r}+0=b Ax=A(xr+xn)=Axr+0=b, b b b是列空间中的向量。所以矩阵 A m × n A_{m\times n} Am×n的作用就是把 C ( A T ) C(A^{T}) C(AT)空间中的向量映射到 C ( A ) C(A) C(A)空间。第六章会定义伪逆 A + A^{+} A+, A + A x = x A^{+}Ax=x A+Ax=x。
2. 向量投影到向量

向量 b b b向向量 a a a的投影,设 x = ∣ ∣ p ∣ ∣ ∣ ∣ a ∣ ∣ x=\frac{||p||}{||a||} x=∣∣a∣∣∣∣p∣∣,即 x x x为 b b b在 a a a上的投影向量 p p p的模除以 a a a的模,所以 p = x a p=xa p=xa,不难看出, a T e = a T ( b − p ) = a T ( b − x a ) = 0 a^{T}e=a^{T}(b-p)=a^{T}(b-xa)=0 aTe=aT(b−p)=aT(b−xa)=0所以 x = a T b a T a x=\frac{a^{T}b}{a^{T}a} x=aTaaTb故 p = x a = a T b a T a a = a a T b a T a = a a T a T a b = P b p=xa=\frac{a^{T}b}{a^{T}a}a=a\frac{a^{T}b}{a^{T}a}=\frac{aa^{T}}{a^{T}a}b=Pb p=xa=aTaaTba=aaTaaTb=aTaaaTb=Pb这里一定要意识到 a T b a^{T}b aTb是一个数,所以向量 a a a可以提到前面,再用结合律即可。
这样我们就推出了向量 b b b投影到向量 a a a的投影矩阵 P = a a T a T a P=\frac{aa^{T}}{a^{T}a} P=aTaaaT P P P矩阵对称且满足 P 2 = P P^{2}=P P2=P,可见该投影矩阵和向量 b b b没有任何关系,如果向量 a = ( c o s θ , s i n θ ) a=(cos\theta,sin\theta) a=(cosθ,sinθ),则 P = [ c 2 c s c s s 2 ] P=\left[ \begin{matrix} c^{2} & cs\\ cs & s^{2} \end{matrix} \right] P=[c2cscss2],和第二章的二维投影矩阵吻合。
3. 向量投影到列空间与最小二乘法
3.1. 向量投影到列空间
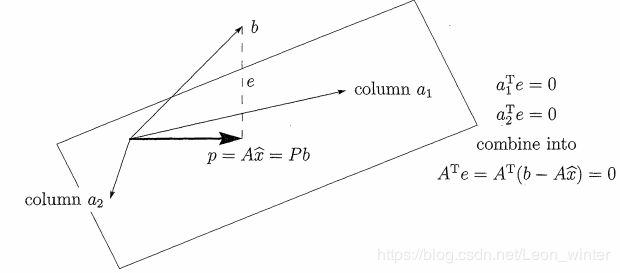
向量 b b b投影到矩阵 A A A的列空间,设投影向量是 A x ^ A\widehat{x} Ax ,其中 x ^ \widehat{x} x 在 A A A的行空间,则向量 e = ( b − A x ^ ) e=(b-A\widehat{x}) e=(b−Ax )垂直 A A A的列空间,所以向量 e e e在矩阵 A A A的左零空间,所以 A T e = A T ( b − A x ^ ) = 0 A^{T}e=A^{T}(b-A\widehat{x})=0 ATe=AT(b−Ax )=0所以我们得到 A T b = A T A x ^ A^{T}b=A^{T}A\widehat{x} ATb=ATAx
如果向量 b b b不在矩阵 A A A的列空间,即 e ≠ 0 e\neq 0 e̸=0,此时 A x = b Ax=b Ax=b无解,那么向量 b b b在矩阵 A A A的列空间的投影向量 A x ^ A\widehat{x} Ax 最接近 b b b,所以 A x = b Ax=b Ax=b的近似方程是 A x = A x ^ Ax=A\widehat{x} Ax=Ax , A x = b Ax=b Ax=b近似解即为 x ^ \widehat{x} x ,其依据就是最小二乘法(最小平方和),此时 ∣ ∣ e ∣ ∣ ||e|| ∣∣e∣∣最小,所以我们有了求 x ^ \widehat{x} x 的一般方程 A T b = A T A x ^ A^{T}b=A^{T}A\widehat{x} ATb=ATAx 如果 A T A A^{T}A ATA可逆,那么 x ^ = ( A T A ) − 1 A T b \widehat{x}=(A^{T}A)^{-1}A^{T}b x =(ATA)−1ATb我们进一步知道了求向量 b b b到 A A A的列空间的投影向量 p = A x ^ = A ( A T A ) − 1 A T b = P b p=A\widehat{x}=A(A^{T}A)^{-1}A^{T}b=Pb p=Ax =A(ATA)−1ATb=Pb其中 P = A ( A T A ) − 1 A T P=A(A^{T}A)^{-1}A^{T} P=A(ATA)−1AT为投影矩阵,该投影矩阵是对称矩阵同时满足 P 2 = P P^{2}=P P2=P。
所以向量不论是向空间投影,还是向另一个向量投影,投影矩阵均满足对称矩阵且 P 2 = P P^{2}=P P2=P。
3.2. 最小二乘法问题
假设求解下面的方程组,
{ 2 x = b 1 3 x = b 2 4 x = b 3 \begin{cases} 2x=b_{1}\\ 3x=b_{2} \\ 4x=b_{3} \end{cases} ⎩⎪⎨⎪⎧2x=b13x=b24x=b3
该方程无解,但是想求其近似解。
3.2.1. 代数法
我们用代数法,利用最小平方和求解,其误差是 E 2 = ( 2 x − b 1 ) 2 + ( 3 x − b 2 ) 2 + ( 4 x − b 3 ) 2 E^{2}=(2x-b_{1})^{2}+(3x-b_{2})^{2}+(4x-b_{3})^{2} E2=(2x−b1)2+(3x−b2)2+(4x−b3)2对其求导取极值点 x ^ = 2 b 1 + 3 b 2 + 4 b 3 2 2 + 3 2 + 4 2 \widehat{x}=\frac{2b_{1}+3b_{2}+4b_{3}}{2^2+3^2+4^2} x =22+32+422b1+3b2+4b3
3.2.2. 矩阵法
我们用代数法,利用最小平方和求解, a x = [ 2 3 4 ] x = [ b 1 b 2 b 3 ] = b ax=\left[ \begin{matrix} 2\\ 3\\ 4 \end{matrix} \right]x=\left[ \begin{matrix} b_{1}\\ b_{2}\\ b_{3} \end{matrix} \right]=b ax=⎣⎡234⎦⎤x=⎣⎡b1b2b3⎦⎤=b
其解就是向量 b b b在 a a a列空间上的投影,在映射回 a a a的行空间,其一般方程为 a T b = a T a x ^ a^{T}b=a^{T}a\widehat{x} aTb=aTax 所以近似解为 x ^ = a T b a T a \widehat{x}=\frac{a^{T}b}{a^{T}a} x =aTaaTb,直接就可以求出来。
4. 正交基,Gram-Schmidt正交化法
4.1. 正交基
4.1.1. 正交矩阵
正交矩阵是列向量相互正交且列向量模为1的矩阵;正交方阵是限定为方阵的正交矩阵,记为 Q Q Q,一般提及正交矩阵默认就是正交方阵,这篇blog后面提及的正交矩阵也是正交方阵。
正交矩阵有如下性质
- Q T Q = 1 Q^{T}Q=1 QTQ=1
- Q T = Q − 1 Q^{T}=Q^{-1} QT=Q−1
4.1.2. 正交变换
正交矩阵 Q Q Q作为变换矩阵,乘以向量x,称为正交变换。正交变换不改变向量 x x x的角度和长度。
4.1.3. 正交矩阵列空间的正交基
考虑正交变换 Q x = [ q 1 , q 2 … q n ] x = b Qx=\left[ \begin{matrix} q_{1},q_{2}\dots q_{n} \end{matrix} \right]x=b Qx=[q1,q2…qn]x=b
其中 q i q_{i} qi均是相互正交的单位列向量,则 x = Q − 1 b = Q T b = [ q 1 T q 2 T ⋅ ˙ ˙ q n T ] b = [ q 1 T b q 2 T b ⋅ ˙ ˙ q n T b ] x=Q^{-1}b=Q^{T}b=\left[ \begin{matrix} q_{1}^{T}\\ q_{2}^{T}\\ \dot{\dot{·}}\\ q_{n}^{T} \end{matrix} \right]b=\left[ \begin{matrix} q_{1}^{T}b\\ q_{2}^{T}b\\ \dot{\dot{·}}\\ q_{n}^{T}b \end{matrix} \right] x=Q−1b=QTb=⎣⎢⎢⎡q1Tq2T⋅˙˙qnT⎦⎥⎥⎤b=⎣⎢⎢⎡q1Tbq2Tb⋅˙˙qnTb⎦⎥⎥⎤
所以 b = Q x = [ q 1 , q 2 … q n ] [ q 1 T b q 2 T b ⋅ ˙ ˙ q n T b ] = [ ( q 1 T b ) q 1 ( q 2 T b ) q 2 ⋅ ˙ ˙ ( q n T b ) q n ] b=Qx=\left[ \begin{matrix} q_{1},q_{2}\dots q_{n} \end{matrix} \right]\left[ \begin{matrix} q_{1}^{T}b\\ q_{2}^{T}b\\ \dot{\dot{·}}\\ q_{n}^{T}b \end{matrix} \right]=\left[ \begin{matrix} (q_{1}^{T}b)q_{1}\\ (q_{2}^{T}b)q_{2}\\ \dot{\dot{·}}\\ (q_{n}^{T}b)q_{n} \end{matrix} \right] b=Qx=[q1,q2…qn]⎣⎢⎢⎡q1Tbq2Tb⋅˙˙qnTb⎦⎥⎥⎤=⎣⎢⎢⎡(q1Tb)q1(q2Tb)q2⋅˙˙(qnTb)qn⎦⎥⎥⎤
由于 q i q_{i} qi是单位列向量,所以 ( q i T b ) q i (q_{i}^{T}b)q_{i} (qiTb)qi是向量 b b b在向量 q i q_{i} qi上的投影向量( q i T b q i T q i q i = q i T b q i \frac{q_{i}^{T}b}{q_{i}^{T}q_{i}}q_{i}=q_{i}^{T}bq_{i} qiTqiqiTbqi=qiTbqi),所以向量 b b b向 q 1 , q 2 … q n q_{1},q_{2}\dots q_{n} q1,q2…qn的各自的投影向量形成的向量 ( ( q 1 T b ) q 1 , ( q 2 T b ) q 2 … ( q n T b ) q n ) T ((q_{1}^{T}b)q_{1},(q_{2}^{T}b)q_{2}\dots(q_{n}^{T}b)q_{n})^{T} ((q1Tb)q1,(q2Tb)q2…(qnTb)qn)T就是 b b b自己,所以 q 1 , q 2 … q n q_{1},q_{2}\dots q_{n} q1,q2…qn就是 Q Q Q的列空间的标准正交基。
4.2. Schmidt正交化法(施密特正交化法)
由一组相互独立的向量产生标准正交向量的方法。具体来看,给定独立的一组向量 a , b , c , d … a,b,c,d\dots a,b,c,d…标准正交的第一个向量就是单纯的标准化即可 q 1 = a ∣ ∣ a ∣ ∣ q_{1}=\frac{a}{||a||} q1=∣∣a∣∣a第二个标准正交向量的产生是在 q 1 q_{1} q1基础上的 A 2 = b − ( q 1 T b ) q 1 q 2 = A 2 ∣ ∣ A 2 ∣ ∣ A_{2}=b-(q_{1}^{T}b)q_{1}\\q_{2}=\frac{A_{2}}{||A_{2}||} A2=b−(q1Tb)q1q2=∣∣A2∣∣A2第三个标准正交向量的产生是在 q 1 q_{1} q1与 q 2 q_{2} q2基础上的 A 3 = c − ( q 1 T c ) q 1 − ( q 2 T c ) q 2 q 3 = A 3 ∣ ∣ A 3 ∣ ∣ A_{3}=c-(q_{1}^{T}c)q_{1}-(q_{2}^{T}c)q_{2}\\q_{3}=\frac{A_{3}}{||A_{3}||} A3=c−(q1Tc)q1−(q2Tc)q2q3=∣∣A3∣∣A3
… \dots …
A j = a j − ( q 1 T a j ) q 1 − ( q 2 T a j ) q 2 − ⋯ − ( q j − 1 T a j ) q j − 1 q j = A j ∣ ∣ A j ∣ ∣ A_{j}=a_{j}-(q_{1}^{T}a_{j})q_{1}-(q_{2}^{T}a_{j})q_{2}-\dots-(q_{j-1}^{T}a_{j})q_{j-1} \\q_{j}=\frac{A_{j}}{||A_{j}||} Aj=aj−(q1Taj)q1−(q2Taj)q2−⋯−(qj−1Taj)qj−1qj=∣∣Aj∣∣Aj
后面产生的标准正交向量是踩在前面的已经产生的标准正交向量上面产生的。
4.3. 矩阵的正交分解
对矩阵 A A A,其列向量要求线性无关,有正交分解
A = Q R A=QR A=QR
其中 Q Q Q是正交矩阵, R R R是上三角矩阵。其基本思路就是对A的列向量进行Schmidt正交化法,以三阶为例 A = [ a , b , c ] = [ q 1 , q 2 , q 3 ] [ q 1 T a q 1 T b q 1 T c 0 q 2 T b q 2 T c 0 0 q 3 T c ] = Q R A=[a,b,c]=[q_{1},q_{2},q_{3}]\left[ \begin{matrix} q_{1}^{T}a & q_{1}^{T}b & q_{1}^{T}c\\ 0 & q_{2}^{T}b & q_{2}^{T}c\\ 0 & 0 & q_{3}^{T}c \end{matrix} \right]=QR A=[a,b,c]=[q1,q2,q3]⎣⎡q1Ta00q1Tbq2Tb0q1Tcq2Tcq3Tc⎦⎤=QR
R R R的对角线元素的乘积是 A A A的列向量构成的多面体的体积。我们可以通过推广平行四边形的面积求法来理解,平行四边形的面积是底乘以高,平行六面体的体积是底乘以高在乘以垂直这条底和高的第三条高, … \dots …, q 1 T a q_{1}^{T}a q1Ta可以理解成底, q 2 T b q_{2}^{T}b q2Tb是垂直于 q 1 T a q_{1}^{T}a q1Ta的高, q 3 T c q_{3}^{T}c q3Tc是垂直于 q 1 T a q_{1}^{T}a q1Ta和 q 2 T b q_{2}^{T}b q2Tb的第三条高 … \dots …,相乘就是体积。
4.4. Hilbert空间
把 R n → R ∞ R^{n}\rightarrow R^{\infty} Rn→R∞,即Hilbert空间中的向量是无穷维的,Hilbert空间包含所有的无穷维向量。
5. 应用:快速傅里叶变换(FFT)
FFT可以说是20世纪发现的算法中,重要程度排名前三的算法。这里从傅里叶级数开始,引出FFT。
5.1. 傅里叶级数
我们先看向量空间V,向量 b b b在V中,V中有基 q 1 , q 2 … q n q_{1},q_{2}\dots q_{n} q1,q2…qn,则 b = x 1 q 1 + x 2 q 2 + ⋯ + x n q n b=x_{1}q_{1}+x_{2}q_{2}+\dots +x_{n}q_{n} b=x1q1+x2q2+⋯+xnqn。
类比上面的向量空间,设函数空间F,函数 f f f在函数空间F中,F中有基 1 , c o s x , s i n x , c o s 2 x , s i n 2 x , c o s 3 x … 1,cosx,sinx,cos2x,sin2x,cos3x \dots 1,cosx,sinx,cos2x,sin2x,cos3x…,F的维度是 ∞ \infty ∞,则 f = a 0 + a 1 c o s x + b 1 s i n x + a 2 c o s 2 x + b 2 s i n 2 x + … f=a_{0}+a_{1}cosx+b_{1}sinx+a_{2}cos2x+b_{2}sin2x+\dots f=a0+a1cosx+b1sinx+a2cos2x+b2sin2x+…, f f f用F中的基表示的等式的系数,就是傅里叶级数。
同时,类比的还有向量内积 ⟶ \longrightarrow ⟶函数内积,向量正交 ⟶ \longrightarrow ⟶函数正交。 向 量 内 积 : v T w = v 1 w 1 + v 2 w 2 … v n w n 向量内积:v^{T}w=v_{1}w_{1}+v_{2}w_{2}\dots v_{n}w_{n} 向量内积:vTw=v1w1+v2w2…vnwn ↓ \downarrow ↓ 函 数 内 积 : ∫ 0 2 π f ( x ) g ( x ) d x 函数内积:\int_{0}^{2\pi}f(x)g(x)dx 函数内积:∫02πf(x)g(x)dx
向 量 正 交 : v T w = 0 向量正交:v^{T}w=0 向量正交:vTw=0 ↓ \downarrow ↓ 函 数 正 交 : ∫ 0 2 π f ( x ) g ( x ) d x = 0 函数正交:\int_{0}^{2\pi}f(x)g(x)dx=0 函数正交:∫02πf(x)g(x)dx=0
傅里叶级数求解有对应的公式,这里不是重点就不列出,百度就行。
傅里叶变换利用傅里叶级数,把信号进行傅里叶分解,就知道了信号在各个频率分量上的占比(傅里叶级数)。
5.2. 离散傅里叶变换
利用傅里叶级数的的傅里叶变换维度是无限维的,这一点在工程应用中十分不便,因此提出了维度是有限长的快速傅里叶变换。
输入: Y = [ y 0 , y 1 , y 2 … y n − 1 ] Y=[y_{0},y_{1},y_{2}\dots y_{n-1}] Y=[y0,y1,y2…yn−1], Y Y Y是对原连续信号采样,采样越密,越能表示原信号。
输出: C = [ c 0 , c 1 , c 2 … c n − 1 ] C=[c_{0},c_{1},c_{2}\dots c_{n-1}] C=[c0,c1,c2…cn−1]
线性关系: F C = Y FC=Y FC=Y, F F F为傅里叶矩阵,是对称复矩阵,也是复矩阵最有名的应用。
傅里叶矩阵 F n F_{n} Fn如下 F n = [ 1 1 1 … 1 1 w n w n 2 … w n n − 1 ⋅ ˙ ˙ ⋅ ˙ ˙ 1 w n n − 1 w n 2 ( n − 1 ) … w n ( n − 1 ) ( n − 1 ) ] F_{n}=\left[ \begin{matrix} 1 & 1 & 1 & \dots & 1\\ 1 & w_{n} & w^{2}_{n} & \dots & w^{n-1}_{n}\\ \dot{\dot{·}}&&&&\dot{\dot{·}}\\ 1 & w^{n-1}_{n} & w^{2(n-1)}_{n} & \dots &w_{n}^{(n-1)(n-1)} \end{matrix} \right] Fn=⎣⎢⎢⎡11⋅˙˙11wnwnn−11wn2wn2(n−1)………1wnn−1⋅˙˙wn(n−1)(n−1)⎦⎥⎥⎤其中 ( F n ) i j = w i j , i , j = 0 , 1 … n − 1 (F_{n})_{ij}=w^{ij},i,j=0,1 \dots n-1 (Fn)ij=wij,i,j=0,1…n−1,且 w n n = 1 w^{n}_{n}=1 wnn=1,即 w n = e i 2 π n w_{n}=e^{i\frac{2\pi}{n}} wn=ein2π。下面是n=4时的傅里叶矩阵 F 4 F_{4} F4, w 4 = e i π 2 = i w_{4}=e^{i\frac{\pi}{2}}=i w4=ei2π=i, F 4 = [ 1 1 1 1 1 i − 1 − i 1 − 1 1 − 1 1 − i − 1 i ] F_{4}=\left[ \begin{matrix} 1 & 1 & 1 & 1\\ 1 & i & -1 & -i\\ 1 & -1 & 1 &-1\\ 1 & -i & -1 & i \end{matrix} \right] F4=⎣⎢⎢⎡11111i−1−i1−11−11−i−1i⎦⎥⎥⎤
同时,傅里叶矩阵 F n F_{n} Fn的逆的求解也很方便: F n − 1 = 1 n F n ‾ F_{n}^{-1}=\frac{1}{n}\overline{F_{n}} Fn−1=n1Fn其中 F n ‾ \overline{F_{n}} Fn为 F n F_{n} Fn的共轭。
5.3. 快速傅里叶变换
离散傅里叶变换需要 n 2 n^{2} n2个乘法,下面给出一种利用矩阵分解化简乘法运算次数的方法。以n=64为例,且 w 64 2 = w 32 w_{64}^{2}=w_{32} w642=w32,傅里叶矩阵 F 64 F_{64} F64分解如下:
[ F 64 ] = [ I D 32 I − D 32 ] [ F 32 0 0 F 32 ] [ P 64 ] = [ I D 32 I − D 32 ] [ I D 16 0 0 I − D 16 0 0 0 0 I D 16 0 0 I − D 16 ] [ F 16 0 0 0 0 F 16 0 0 0 0 F 16 0 0 0 0 F 16 ] [ P 32 0 0 P 32 ] [ P 64 ] … \begin{aligned} \left[ \begin{matrix} F_{64} \end{matrix} \right]&=\left[ \begin{matrix} I & D_{32}\\ I & -D_{32} \end{matrix} \right]\left[ \begin{matrix} F_{32} & 0\\ 0 & F_{32} \end{matrix} \right]\left[ \begin{matrix} P_{64} \end{matrix} \right] \\ &=\left[ \begin{matrix} I & D_{32}\\ I & -D_{32} \end{matrix} \right]\left[ \begin{matrix} I & D_{16} & 0 & 0\\ I & -D_{16} & 0 & 0\\ 0 & 0 & I & D_{16}\\ 0 & 0 & I & -D_{16} \end{matrix} \right]\left[ \begin{matrix} F_{16} & 0 & 0 & 0\\ 0 & F_{16} & 0 & 0\\ 0 & 0 & F_{16} & 0\\ 0 & 0 & 0 & F_{16} \\ \end{matrix} \right]\left[ \begin{matrix} P_{32} & 0\\ 0 & P_{32} \end{matrix} \right]\left[ \begin{matrix} P_{64} \end{matrix} \right] \\ & \dots \end{aligned} [F64]=[IID32−D32][F3200F32][P64]=[IID32−D32]⎣⎢⎢⎡II00D16−D160000II00D16−D16⎦⎥⎥⎤⎣⎢⎢⎡F160000F160000F160000F16⎦⎥⎥⎤[P3200P32][P64]…
其中 P P P是置换矩阵,把偶数行提到奇数行前的置换矩阵, D D D是对角矩阵, D n = [ 1 w w 2 ⋅ w n − 1 ] D_{n}=\left[ \begin{matrix} 1\\ &w\\ &&w^{2}\\ &&&·\\ &&&&w^{n-1} \end{matrix} \right] Dn=⎣⎢⎢⎢⎢⎡1ww2⋅wn−1⎦⎥⎥⎥⎥⎤
考虑乘法运算, 6 4 2 次 乘 法 ⟶ 32 + 3 2 2 + 0 ⟶ 32 + ( 16 + 1 6 2 × 2 ) × 2 = 32 + 32 + 1 6 2 × 4 ⟶ 32 + 32 + ( 8 + 8 2 × 2 ) × 4 = 32 + 32 + 32 + 8 2 × 8 … ⟶ 6 × 32 + 64 \begin{aligned} 64^{2}次乘法&\longrightarrow32+32^{2}+0 \\ &\longrightarrow 32+(16+16^{2}\times 2)\times 2=32+32+16^{2}\times 4 \\ &\longrightarrow32+32+(8+8^{2}\times 2)\times 4 = 32+32+32+8^{2}\times 8\\ &\dots \\ &\longrightarrow 6\times 32+64 \end{aligned} 642次乘法⟶32+322+0⟶32+(16+162×2)×2=32+32+162×4⟶32+32+(8+82×2)×4=32+32+32+82×8…⟶6×32+64注意这里乘以 I I I和 P P P开销不大,因此在考虑乘法运算开销时没有考虑(乘法开销记为0)。故FFT使得乘法运算次数变为 n 2 ⟶ n 2 l o g 2 n + n = O ( n l o g n ) n^{2}\longrightarrow \frac{n}{2}log_{2}^{n}+n=O(nlogn) n2⟶2nlog2n+n=O(nlogn)
以n=1024为例,这在计算机实际应用中根本不算大的数字,但FFT使得其乘法运算次数减少近200倍。
参考书籍
《Linear Algebra and Its Applications》