python 数据结构四 之 二叉树和树
python数据结构教程第四课
树形结构是复杂结构中最简单的一类,这是一类非常重要的结构,在实际中使用广泛,反映了许多计算过程的抽象结构
一、简介
1.树
2.二叉树
二、二叉树和树的抽象数据类型(ADT)
三、二叉树的python实现
1.二叉树的list实现
2.二叉树的遍历操作
3.二叉树的链表实现
四、二叉树的应用——Huffman Tree
五、树的python实现
一、简介
二叉树是树的子集,具有树的全部特性,这里先介绍树的定义与基本特性
1.树
定义:一棵树是n(n>=0)个结点的有限集T,当T非空时满足:
1)T中有且仅有一个特殊结点r称为树T的根
2)除根结点外的其余结点分为m(m>=0)个互不相交的非空有限子集,每个集合为一棵非空树,称为r的子树
结点个数为0的树称为空树
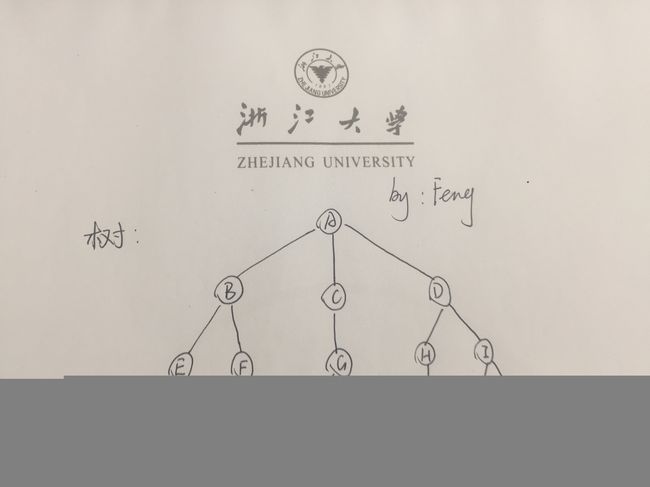
树的特性:
1)如果树的结构不空,其中就存在着唯一的起始结点,称为树根
2)按结构的连接关系,树根外的其余结点都有且只有一个前驱,但另一方面,一个结点可以有0个或者多个后继。在非空的树结构中一定有一些结点并不连接到其他结点,与尾结点相似
3)从树根结点出发,经过若干次后继关系可以到达结构中的任意一点
4)结点之间的联系不会形成循环关系
5)从这个结构里的任意两个不同结点出发,通过后继关系可达的两个结点集合,或者互不相交,或者一个是另一个的子集
2.二叉树
定义:二叉树是结点的有穷集合。这个集合或者是空集,或者其中有一个称为根结点的特殊结点,其余结点分属两棵不相交的二叉树,这两棵二叉树分别是原二叉树的左子树和右子树
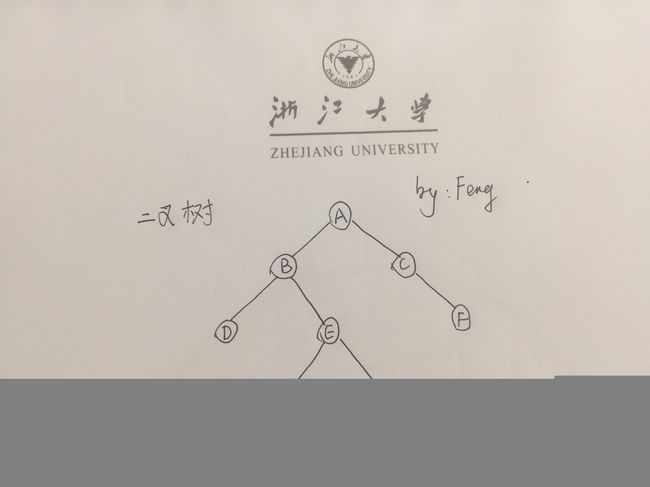
关于二叉树的一些基本概念:
1)一棵二叉树的根结点称为该树的子树根结点的父结点;与此对应,子树的根结点称为二叉树树根结点的子结点
2)从父结点到子结点有一条连线,称为从父结点到子结点的边,父结点的两个结点互为兄弟结点
3)在二叉树里有些结点的两棵子树都空,没有子结点,这种结点称为树叶,树中其余结点称为分支结点
4)一个结点的子结点个数称为该结点的度数。显然,二叉树中树叶结点的度数为0,分支结点的度数可以是1或2
二、二叉树和树的抽象数据类型(ADT)
二叉树的基本操作包括创建空树,设置左右子树等,其基本ADT如下:
ADT BTree:
BTree(self, data, left,right) #构造空树
is_empty(self) #空树判断
num_nodes(self) #返回结点树
data(self) #返回树根数据
left(self) #返回左子树
right(self) #返回右子树
set_left(self) #设置左子树
set_right() #设置右子树
traversal(self) #迭代器
forall(self,op) #op的遍历操作树的抽象数据类型与二叉树类似,不过在具体实现时,实现策略会有所不同,这里先给出ADT:
ADT Tree:
Tree(self, data,forest) #树的初始化
is_empty(self) #空树判断
num_nodes(self) #返回结点数据
data(self) #返回树根中的数据
first_child(self,node) #取得node的第一棵子树
children(self,node) #结点node子树的迭代器
set_first(self,tree) #用tree取代第一棵子树
insert_child(self, i,tree) #设置第i棵子树
traversal(self) #所有结点的迭代器
forall(self,op) #op的遍历操作本文会着重介绍二叉树的实现方法和操作,由于篇幅问题对于树的实现只做简单的策略介绍,感兴趣的同学可以等待我以后另开博客讲解
三、二叉树的python实现
1.二叉树的list实现
思考可以发现,二叉树的一个结点其实就是一个三元组,分别存储着数据和左右子树,因此这里给出一个简单的list二叉树实现方式(也可以用tuple实现,区别只是在于list可以改变)
采用嵌套括号的形式,可以将二叉树表示为:
['A',['B',None,None],
['C',['D',['F',None,None],
['G',None,None]],
['E',['I',None,None],
['H',None,None]]]]由上,我们来定义一组函数,描述二叉树的基本构造与方法,其具体的类实现,会在介绍了二叉树的遍历之后,使用链表方法实现
def BTree(data,left=None,right = None):
return [data,left,right]
def is_empt_BTree(btree):
return btree is None
def root(btree):
return btree[0]
def left(btree):
return btree[1]
def right(btree):
return btree[2]
def set_root(btree,data):
btree[0] = data
def set_left(btree,data):
btree[1] = data
def set_right(btree,data):
btree[2] = data
定义一个二叉树的源码为:
t1 = BTree(2,BTree(4),BTree(8))2.二叉树的遍历
二叉树的结构比较复杂,因此系统化遍历有许多种可能的方式,以根为起点,存在两种基本方式:
1)深度优先遍历,顺着一条路径尽可能向前搜索,必要时回朔。对于二叉树,最基本的回朔情况是检查完一个结点,由于无路可走便回头
2)宽度优先遍历,在所有路径上齐头并进
按深度优先遍历需要做三件事情:遍历左子树、遍历右子树和访问根结点,选择这三项工作不同的执行顺序,就可以得到三种常见的遍历顺序:先根序遍历、中根序遍历、后根序遍历;对二叉树做宽度优先遍历,就是按二叉树的层次逐层访问树中的各结点,常见的是在每一层从左往右逐个访问
下面给出先根序遍历二叉树的递归函数:
#先给出二叉树结点类的定义
class BNode:
def __init__(self,data,left = None,right = None):
self._data = data
self._left = left
self._right = right
def data(self):
if self is None:
return None
else:
return self._data
def left(self):
if self is None:
return None
else:
return self._left
def right(self):
if self is None:
return None
else:
return self._right
def set_data(self,data):
self._data = data
def set_left(self,left):
self._left = left
def set_right(self,right):
self._right = right
def __eq__(self,another):
if self is None:
return another == None
if another is None:
return self is None
else:
return self._data == another.data() and self._left == another.left() and self._right == another.right()
#递归遍历,先根序,proc是对结点中元素的操作
def preorder(t,proc):
if t is None:
return
proc(t.data())
preorder(t.left())
preorder(t.right())测试函数
#使用了上述递归算法思想的二叉树输出函数
def print_BNode(t):
if t is None:
print('^',end = '')
return
print('(' + str(t.data()),end = '')
print_BNode(t.left())
print_BNode(t.right())
print(')',end='')
t = BNode(1,BNode(2,BNode(5)),BNode(3))
print_BNode(t)结果
(1(2(5^^)^)(3^^))下面给出宽度优先遍历的二叉树遍历函数:
def levelorder(t,proc):
qu = SQueue()
qu.enqueue(t)
while not qu.is_empty():
t = qu.dequeue()
if t is None: #弹出的树为空则直接跳过
continue
qu.enqueue(t.left())
qu.enqueue(t.right())
proc(t.data())当我们使用非递归算法实现二叉树的遍历时,算法的过程和结构会更加清晰,这里仅给出先根序遍历的非递归算法
def preorder_nonrec(t,proc):
s = SStack()
while t is not None or not s.is_empty():
while t is not None:
proc(t.data())
s.push(t.right())
t = t.left()
t = s.pop()3.二叉树的链表实现
在熟悉了二叉树的遍历算法之后,我们便可以较为完整利用链表实现二叉树类,二叉树的结点继续使用前面的结点类,没有任何问题
#二叉树的基本链表实现类定义
class BTree:
def __init__(self,data,left = None,right = None):
if data == None:
self._root = None
self._num = 0
else:
self._root = BNode(data,left,right)
self._num = 1
#空链表判断
def is_empty(self):
return self._num == 0
#获得根结点中的数据
def root(self):
if self.is_empty():
return None
else:
return self._root.data()
#获得根结点的左子树
def left(self):
if self.is_empty():
return None
else:
return self._root.left()
#获得根结点的右子树
def right(self):
if self.is_empty():
return None
else:
return self._root.right()
#设置根结点的根
def set_root(self,root):
self._root = root
#设置根结点的左子树
def set_left(self,left):
self._root.set_left(left)
#设置根结点的右子树
def set_right(self,right):
self.set_right(right)
#先根序遍历方法
def preorder_elements(self):
t,s = self._root,SStack()
while t is not None or not s.is_empty():
while t is not None:
s.push(t.right())
yield t.data()
t = t.left()
t = s.pop()
#层次序遍历方法
def levelorder(self):
qu = SQueue()
qu.enqueue(self._root)
while not qu.is_empty():
t = qu.dequeue()
if t is None:
continue
qu.enqueue(t.left())
qu.enqueue(t.right())
yield t.data()
#两棵树的结构数据都相等时,两棵树相等
def __eq__(self,another):
def preorder_node(Tree):
t,s = Tree._root,SStack()
while t is not None or not s.is_empty():
while t is not None:
s.push(t.right())
yield t
t = t.left()
t = s.pop()
lt1 = []
lt2 = []
for i in preorder_node(self):
lt1.append(i)
for i in preorder_node(another):
lt2.append(i)
if len(lt1) != len(lt2):
return False
i = 0
while i < len(lt1):
if lt1[i] != lt2[i]:
return False
return True
#返回克隆树
def clone(self):
return copy.deepcopy(self)
#分别返回根结点和分支结点的数目
def count_nodes(self):
def preorder_node(Tree):
t,s = Tree._root,SStack()
while t is not None or not s.is_empty():
while t is not None:
s.push(t.right())
yield t
t = t.left()
t = s.pop()
count_leaf = 0
count_nleaf = 0
for i in preorder_node(self):
if i.left() == None and i.right() == None:
count_leaf += 1
else:
count_nleaf += 1
return count_leaf,count_nleaf
#输出树的所有结点
def printall(self):
for i in self.preorder_elements():
print(i,end = ' ')测试代码
T = BTree(10,BNode(3,BNode(6)),BNode(5))
for i in T.levelorder():
print(i,end = ' ')
T2 = BTree(10,BNode(4,BNode(6)),BNode(5))
print()
print(T == T2)
print(T.count_nodes())结果
10 3 5 6
False
(2, 2)四、二叉树的应用——Huffman Tree
Huffman Tree(哈夫曼树),哈夫曼树是信息领域重要的算法,这里首先给出哈夫曼树的定义:
设有实数集W={w0,w1,…,wm-1},T是一棵扩充二叉树,其m个外部结点分别以wi为权,而且T的带权外部路径长度WPL在所有这样的扩充二叉树中达到最小,则称T为数据集W的最优二叉树或者哈夫曼树
哈夫曼提出了一种算法,可以从任意的实数集中构造出与之对应的哈夫曼树,这个构造算法如下:
1)算法的输入为实数集W={w0,w1,…wm-1}
2)在构造中维护一个包含K棵二叉树的集合F,开始时k=m且F={T0,T1,…,Tm-1},其中每个Ti是一棵只包含权为wi的根结点的单点二叉树
3)在算法的过程中重复执行下面两个步骤,直到集合F中剩下一棵树为止:
构造一棵新二叉树,其左右子树是从集合F中选取的两棵权最小的二叉树,其根结点的权值设置为这两棵子树的根结点的权值之和;
将所选的两棵二叉树从F中删除,把新构造的二叉树加入F
下面给出哈夫曼树的实现算法:
#哈夫曼树结点类
class HTNode(BNode):
def __lt__(self,othernode):
return self.data() < other.data()
#哈夫曼树中需要的优先队列
class HuffmanPrioQ(PrioQueue):
def number(self):
return len(self._elems)
#哈夫曼树构造算法
def HuffmanTree(weights):
trees = HuffmanPrioQ()
for w in weights:
trees.enqueue(HTNode(w))
while trees.number() > 1:
t1 = trees.dequeue()
t2 = trees.dequeue()
x = t1.data() + t2.data()
trees.enqueue(HTNode(x,t1,t2))
return trees.dequeue()五、树的python实现
树的结构相对于二叉树来比较复杂,其实现方式也多种多样,比如子结点引用表示法、子结点表表示法、长子-兄弟表示法等,这里仅介绍一种较为简单的子结点引用法
树的最基本表示方法是子结点引用法,其基本设计与二叉树的链接表示法类似:用一个数据单元表示结点,通过结点间的链接表示树结构,通过结点间的链接表示树结构。但这里有一个麻烦:树的结点度数不确定,而且结点的度数差可能很大,在这种情况下,一种简单的考虑是只支持度数不超过固定m的树,也就是说,树中分支结点至多允许m棵子树,其具体的类实现方法与二叉树的类实现方法类似,这里不给出具体的源代码