机器学习算法-PageRank（排序）

Larry Page于1998年提出了PageRank，并在斯坦福大学攻读计算机科学博士学位期间，遇到了Sergey Brin，两人于1998年合伙创立Google，并将PageRank应用在Google搜索引擎的检索结果排序上，该技术也是Google早期最关键的核心技术，已被成功申请专利。Larry Page是Google的创始首席执行官，2001年4月转任现职产品总裁。 2004 年入选美国国家工程学院，2005年，佩奇当选美国艺术与科学院院士。2013年，获选2013美国40岁以下最有影响力CEO，并以230亿美元资产荣登福布斯2013全球富豪榜第二十位。2016年10月，《福布斯》发布”美国400富豪榜”，Larry Page排名第九。简直就是神一般的存在。他目前仍与Eric Schmidt和Sergey Brin一起共同负责 Google的日常运作，算是当今世界将知识创新转化为财富最成功的人之一。

一、基本思想

在Google中搜索“ABC”，搜索引擎工作的简要过程如下：针对查询词“ABC”进行分词“A”、”B”、”C”，根据建立的倒排索引，将同时包含”A”、”B”和”C”的页面返回（通常情况下，搜索引擎在分词后会自动过滤掉一些”停顿词”，如”是”、”的”、”，”等，本处假定“A”、”B”、”C”均是有效关键词。）。通常情况下，同时包含了关键词“A”、”B”、”C”的页面数以千计，假设反馈页面有1000张，那么可能的排列组合就有1000!之多，如果相关的页面被排在了后面，不相关的页面被排在了前面，用户需要遍历浏览几百次才能获取需要的信息，费时费力，体验非常糟糕。针对此如何将查询结果合理的排序，将重要的文档优先反馈给用户，使用户快速获取有用信息便变得非常关键。

但如何度量网页本身的重要性呢？单纯地靠人力去评判是万万不可能的，因此需要基于互联网的特性，再利用机器学习的方法快速地实现页面重要性的评估：互联网上的每一篇HTML文档除了包含文本、图片、视频等信息外，还包含了大量的链接关系，利用这些链接关系，能够发现某些重要的网页。直观地看，某网页1链向网页2，则可以认为网页1觉得网页2有链接价值，是比较重要的网页。某网页被指向的次数越多，则它的重要性越高；越是重要的网页，所链接的网页的重要性也越高。

比如，新华网体育在其首页中对新浪体育做了链接，人民网体育同样在其首页中对新浪体育做了链接。可见，新浪体育被链接的次数较多；同时，人民网体育和新华网体育也都是比较“重要”的网页，因此新浪体育也应该是比较“重要”的网页。PageRank便是一种在搜索引擎中根据网页之间相互的链接关系计算网页重要性排名的技术。（Google在反馈查询结果时，一般是综合考虑各个网页的PageRank值和TF-IDF值。）

二、模型原理

PageRank根据网页之间相互的链接关系来计算网页的排名，是Google用来标识网页的等级或重要性的一种方法。其级别从1到10级，PageRank值越高说明该网页越受欢迎（越重要）。通常，PageRank 0～2表示目前未有太多外部连结连到这个网站，一个PR值为1的网站表明这个网站不太具有流行度；而PageRank值值为7~10则表明这个网站非常受欢迎（或者说极其重要），Google把自己的网站的PageRank值定到9，这说明Google这个网站是非常受欢迎的，也可以说这个网站非常重要。国内百度的PageRank值也是9。一般PageRank值达到4，就算是一个不错的网站了， 已经证明链接到此网站的外部链接“质”、“量”俱佳。在本文中，以0~1之间的数来表示网页的PageRank值（Google其是在此结果的基础上做了一次映射，方便用户一目了然网页的重要性，如0~0.001为0级、0.001~0.01为1级、0.01~0.02为2级……）

通俗地讲PageRank值表明了在互联网上随机地单击链接将会到达特定网页的可能性。通常，能够从更多地方到达的网页更为重要，因此具有更高的PageRank值。如果要查看此站点PageRank值，请安装Google工具条并启用PageRank特性，或者在Firefox安装SearchStatus插件。目前一些网站也可以直接查询指定网页的PageRank值，如本人在站长之家查询个人博客主页的结果如下（看来是沾了CSDN的光）：

PageRank 是基于「从许多优质的网页链接过来的网页，必定还是优质网页」的回归关系，来判定所有网页的重要性。假设一个由只有5个页面组成的集合： P1 ， P2 ， P3 ， P4 和 P5 。如果 P1 ， P2 链向 P3 ，那么 P3 的PR（PageRank）值将是 P1 ， P2 的和。

p3=p1+p2.

继续假设 P1 也有链接到 P4 ，一个页面不能投票2次。所以 P1 给每个页面半票。以同样的逻辑， P2 投出的票只有三分之一算到了 P1 的PageRank上。

p3=p12+p23.

换句话说，根据链出总数平分一个页面的PR值，

p3=p1L1+p2L2.

针对整个互联网，网页数量是5的十亿倍、百亿倍，不过仍然可以把各网页之间的链接关系看成一个有向图，假设冲浪者浏览的下一个网页链接来自于当前网页。因此对于任意网页 Pi ，它的PageRank值可表示为如下：

pi=∑j∈BipjLj

其中 pi ：网页 i 的PageRank值， pj ：网页 j 的PageRank值， Bi 为所有链接到网页 i 的网页集合， Lj 为网页 j 的对外链接数（出度）。

三、矩阵化PageRank问题

互联网是一个有向图，每一个网页是图的一个顶点，网页间的每一个超链接是图的一个有向边，用邻接矩阵来表示图，即：定义邻接矩阵为 G ，若网页 j 到网页 i 有超链接，则 gij=1 ；反之 gij=0 。显然，如果网页有 N 个，则矩阵为 N×N 的0、1方阵。记矩阵 G 的列和、行和分别是

cj=∑igij.

rj=∑jgij.

cj ， ri 分别给出了页面 j 的链出链接数目和链入链接数目。

假设我们在上网的时侯浏览页面并选择下一个页面，这个过程与过去浏览过哪些页面无关，而仅依赖于当前所在的页面，那么这一选择过程可以认为是一个有限状态、离散时间的随机过程，其状态转移规律用Markov链描述。定义转移概率矩阵 A=(aij) ，其中

aij=gijcj,i,j=1,2,…,N.

此时对于任意网页 Pi ，它的PageRank值可表示为如下：

pi=∑j∈Biaijpj.

假定 p 定义为网页的PageRank矢量， pi 表示第 i 个网页的PageRank值，则基于上面的分析，PageRank问题可以矩阵化成如下形式：

Ap=p,∑ipi=1.

观察上面的等式，可以发现 p 即是求矩阵 A 的特征值1对应的特征矢量，因此可以直接求解： (A−I)p=0 。不过互联网网页数量以百亿计，直接对矩阵 A 进行分解求解 p 复杂度太高。那能否找到其他简单高效的方法？观察可知矩阵 A 为随机矩阵，因此1为其最大的特征值，那么便可以通过幂迭代法求解最大特征值1对应的特征向量：给定 p0 ， pk+1=Apk 。此时 limk→∞pk 存在，并且与 p0 的选取无关！具体也可以通过Markov 过程的收敛性来证明。此处省略。

四、PageRank举例

假设世界上只有七张网页，依次编号为ID=1~7，其抽象结构如下图：

网页链接图的邻接矩阵 G ：

G=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢0111101100000011000000110100101101010001000000100⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥.

状态转移概率矩阵 A

A=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢01515151501510000001212000000131301300140141401401200012000000100⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥.

PageRank的计算–直接求解：

p=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢0.6994565338373890.3828604185215180.3239588156720540.2429691117540400.4123112199462510.1030778049865630.139891306767478⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⟹归一化⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢0.3035143769968050.1661341853035140.1405750798722040.1054313099041530.1789137380191690.04472843450479230.0607028753993610⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

PageRank的计算–幂迭代求解

p=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢17171717171717⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥p0⟹⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢0.321428570.147619050.111904760.064285710.290476190.035714290.02857143⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥p1⟹…⟹⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢0.303310470.166277790.140563450.105344470.179159360.044610650.06073381⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥p10⟹…⟹⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢0.303514570.166134160.140575020.105431220.178913820.044728450.06070277⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥p20

可以看到，幂迭代法在经过20次迭代后，取得的结果已经跟直接求解的值十分相近。接下来将 PageRank 的评价按顺序排列(PageRank小数点3位四舍五入)：

名次	PageRank	网页ID	发出链接网页	被链接网页
1	0.304	1	2,3,4,5,7	2,3,5,6
2	0.179	5	1,3,4,6	1,4,6,7
3	0.166	2	1	1,3,4
4	0.141	3	1,2	1,4,5
5	0.105	4	2,3,5	1,5
6	0.061	7	5	1
7	0.045	6	1,5	5

可得页面之间相互关系及状态转移图：

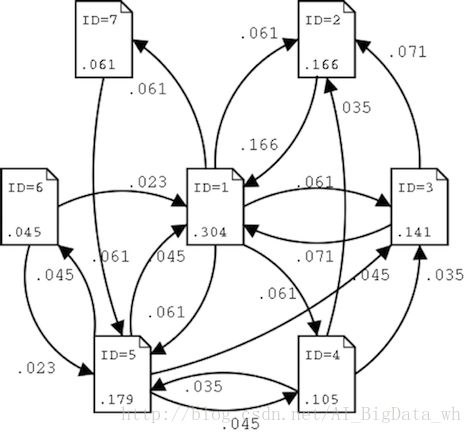
最后让我们详细地看一下， P1 的PageRank 是0.304，占据全体的三分之一，成为了第1位。特别需要说明的是，起到相当大效果的是从排在第3位的 P2 中得到了所有的PageRank (0.166) 数。 P2 有从3个地方过来的链入链接，而只有面向 P1 页面的一个链接，因此 P1 就得到 P2 的所有的PageRank数。不过，就因为 P1 页面是链出链接和链入链接最多的页面，也可以理解它是最受欢迎的页面。反过来，最后一名的 P6 只有 P1 的15％的微弱评价。总之，即使有同样的链入链接的数目，链接源页面评价的高低也影响 PageRank 的高低。

五、PageRank存在的问题

实际的网络超链接环境没有这么理想化，PageRank会面临两个问题：
1. Rank Leak：一个独立的网页如果没有外出的链接（Dead Ends节点）就产生等级泄漏。

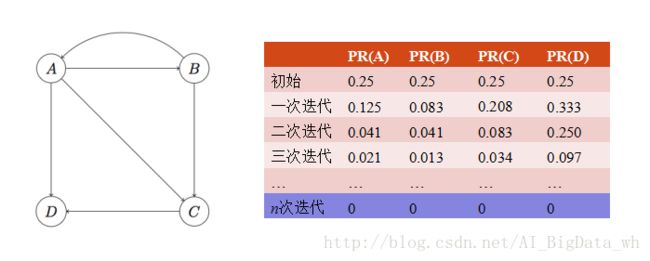
处理Rank Leak的方法一是迭代拿掉图中的Dead Ends节点及Dead Ends节点相关的边（之所以迭代拿掉是因为当目前的Dead Ends被拿掉后，可能会出现一批新的Dead Ends），直到图中没有Dead Ends。对剩下部分计算PageRank值，然后以拿掉Dead Ends逆向顺序反推Dead Ends的PageRank值。以上图为例，首先拿到D和D相关的边，D被拿到后，C就变成了一个新的Dead Ends，于是拿掉C，最终只剩A、B。此时可很容易算出A、B的PageRank值均为1/2。然后我们需要反推Dead Ends的PageRank值，最后被拿掉的是C，可以看到C前置节点有A和B，而A和B的出度分别为3和2，因此C的PageRank值为：1/2 * 1/3 + 1/2 * 1/2 = 5/12；最后，D的PageRank值为：1/2 * 1/3 + 5/12 * 1 = 7/12。所以最终的PageRank值为（1/2, 1/2, 5/12, 7/12），归一化后的结果为（1/4, 1/4, 5/24, 7/24）。

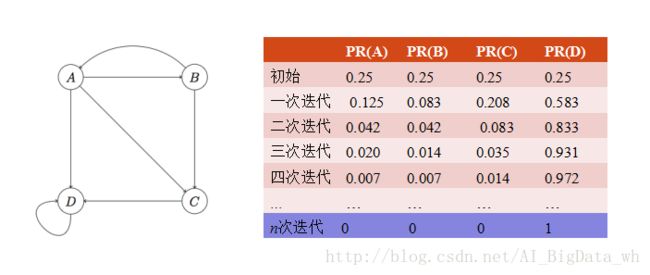
2. Rank Sink：整个网页图中的一组紧密链接成环的网页如果没有外出的链接就产生Rank Sink。如果对这个图进行计算，会发现D的PageRank值越来越大（趋近于1），而其他节点的PageRank值越来越小（趋近于零）。

其实在真实环境中，一个上网者从一个随机的网页开始浏览，接下来不断点击当前网页的链接开始下一次浏览。但是在每一次进行下一个浏览时，上网者有可能因为种种原因开始了一个随机的网页。这种随机模型更加接近于用户的浏览行为。

基于此种更合理的随机模型，可以对上述的PageRank问题进行优化。设定任意两个顶点之间都有直接通路，在每个顶点处以概率 β 按原来蓝色方向转移，以概率 1−β 按红色方向转移。由于网页数目巨大，网页之间的连接关系的邻接矩阵是一个很大的稀疏矩阵，采用邻接表来表示网页之间的连接关系。随机浏览模型的PageRank公式：

pk+1=(βA+(1−β)EN)pk⟹pk+1=βApk+1−βNe.

其中 N 为网络中网页总数； β 是阻尼因子，通常设为0.85， β 即按照超链接进行浏览的概率； 1−β 为随机跳转一个新网页的概率； E 为 N×N 的全1矩阵； e 为 N 维全1矢量。随机模型不仅可以解决Rank Sink问题，对Rank Leak问题也有很好的效果。

一个页面的PageRank值是由其他页面的PageRank值计算到。Google不断的重复计算每个页面的PageRank。如果给每个页面一个随机PageRank值（非0），由于等式 p=A∗p 满足马尔可夫链的性质，且马尔可夫链收敛，则 p 存在唯一解。通过迭代计算得到所有节点的PageRank值，那么经过不断的重复计算，这些页面的PageRank值会趋向于正常和稳定。

六、算法优缺点

PageRank算法是一个与查询无关的静态算法，所有网页的PageRank值通过离线计算获得，其有效减少在线查询时的计算量，极大降低了查询回应时间。排序技术是搜索引擎的绝密，Google目前所使用的排序技术，已经不再是简单的PageRank！不过PageRank的价值是不容置否的，目前已经在各行各业取得广泛的应用，如学术论文的作者的重要性排序–某作者引用了其他作者的文献，则该作者认为其他作者是“重要”的；网络爬虫(Web Crawler)–可以利用PageRank值，决定某个URL，所需要抓取的网页数量和深度，重要性高的网页抓取的页面数量相对多一些，反之，则少一些。

不过PageRank在实际应用中也存在一些缺点，如过分相信链接关系–一些权威网页往往是相互不链接的，比如新浪、搜狐、网易以及腾讯这些大的门户之间，基本是不相互链接的，学术领域也是这样；而且人们的查询具有主题特征，PageRank忽略了主题相关性，导致结果的相关性和主题性降低 ；旧的页面等级会比新页面高。因为即使是非常好的新页面也不会有很多上游链接，除非它是某个站点的子站点。

七、算法实战

偶尔给大家换个口味，本文以R语言进行实战演练。

#构建邻接矩阵
adjacencyMatrix<-function(pages){
  n<-max(apply(pages,2,max))
  A <- matrix(0,n,n)
  for(i in 1:nrow(pages))   
              A[pages[i,]$dist,pages[i,]$src]<-1
  A
}

#变换概率矩阵,考虑d的情况
dProbabilityMatrix<-function(G,d=0.85){
  cs <- colSums(G)
  cs[cs==0] <- 1
  n <- nrow(G)
  delta <- (1-d)/n
  A <- matrix(delta,nrow(G),ncol(G))
  for (i in 1:n) A[i,] <- A[i,] + d*G[i,]/cs
  A
}

#递归计算矩阵特征值
eigenMatrix<-function(G,iter=100){
  iter<-10
  n<-nrow(G)
  x <- rep(1,n)
  for (i in 1:iter) x <- G %*% x
  x/sum(x)
}


src=c(1,1,1,1,1,2,3,3,4,4,4,5,5,5,5,6,6,7)
dist=c(2,3,4,5,7,1,1,2,2,3,5,1,3,4,6,1,5,5)
pages=data.frame(src,dist)

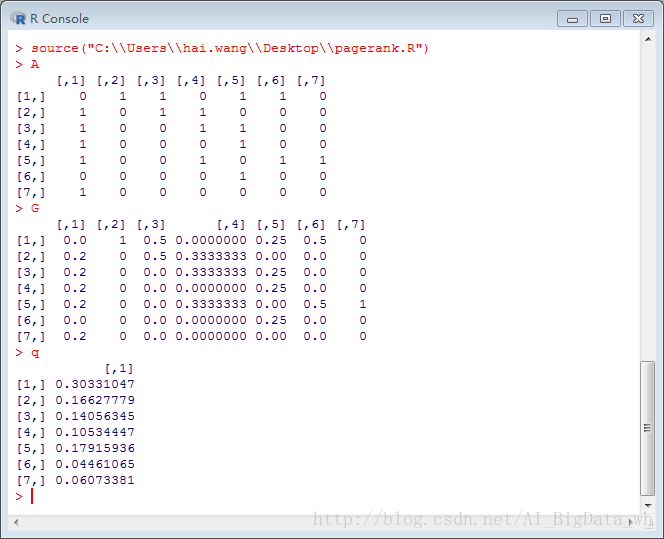
A<-adjacencyMatrix(pages)
G<-probabilityMatrix(A)
q<-eigenMatrix(G,100)

参考资料

1. http://www.cnblogs.com/rubinorth/p/5799848.html PageRank算法–从原理到实现
2. https://en.wikipedia.org/wiki/PageRank PageRank
3. Bing Liu and Philip S. Yu, “The Top Ten Algorithms in Data Mining” Chapter 6.
4. 举例部分基于很早之前下载的一份PPT，在此对作者表示感谢。