hdu 1754 I Hate It 线段树（插点问点）

线段树入门题，年前做过线段树类型的题，不过是用树状数组或者rmq做的，没用线段树(其实是不会)，

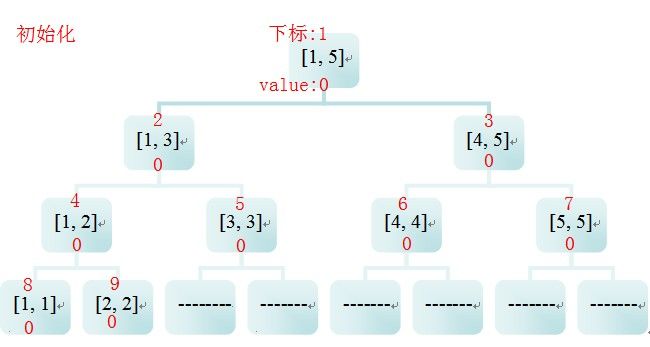
看了这张图原理应该就明白了，
http://blog.csdn.net/x314542916/article/details/7837276(图片来源)
I Hate It

Time Limit: 9000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 60381 Accepted Submission(s): 23503

Problem Description
很多学校流行一种比较的习惯。老师们很喜欢询问，从某某到某某当中，分数最高的是多少。
这让很多学生很反感。

不管你喜不喜欢，现在需要你做的是，就是按照老师的要求，写一个程序，模拟老师的询问。当然，老师有时候需要更新某位同学的成绩。

Input
本题目包含多组测试，请处理到文件结束。
在每个测试的第一行，有两个正整数 N 和 M ( 0

#include
#include
using namespace std;
struct
{
    int left,right,mid,maxn;  //left ，right分别为此区间的最小最大值，mid为此区间的一半，maxn为对应区间的最大值
} w[800010];
int a[200010];
void build(int l,int r,int tr)
{
    if(l==r)
    {
        w[tr].left=w[tr].right=l,w[tr].maxn=a[l];
        return;  //若区间只有一个值，赋值
    }
    w[tr].left=l,w[tr].right=r,w[tr].mid=(l+r)>>1;  //定义左右区间，以及中间值  ，使用位运算比乘法，除法要快
    build(l,w[tr].mid,tr<<1);  //将此区间再分左一半
    build(w[tr].mid+1,r,(tr<<1)+1); //将此区间再分右一半
    w[tr].maxn=max(w[tr<<1].maxn,w[(tr<<1)+1].maxn);  //给这个区间赋值
}
void update(int n,int m,int tr)  //更新区间
{
    if(w[tr].left==n&&w[tr].right==n)  //若找到对应的区间
    {
        w[tr].maxn=m;     //重新赋值
        return ;
    }
    else if(n<=w[tr].mid)  //若n小于此区间的一半
        update(n,m,tr<<1);  //再从此区间的左一半里接着找
    else if(n>w[tr].mid)  //若n大于此区间的一半
        update(n,m,(tr<<1)+1);  //再从此区间的右一半里接着找
    w[tr].maxn=max(w[tr<<1].maxn,w[(tr<<1)+1].maxn);  //更新此区间最大值，即为max(左一半区间的最大值，右一半区间的最大值)
}
int query(int l,int r,int tr)  //查询(l,r)区间max
{
    if(l==w[tr].left&&r==w[tr].right)  //若查到此区间，返回最大值
        return w[tr].maxn;
    else if(r<=w[tr].mid)   //如果r小于区间的一半
        return query(l,r,tr<<1);  //接着从区间左一半里查询所求区间
    else if(l>w[tr].mid)   //如果r大图区间的左一半
        return  query(l,r,(tr<<1)+1);  //接着从区间右一半里查询此区间
    else
        return max(query(l,w[tr].mid,tr<<1),query(w[tr].mid+1,r,(tr<<1)+1));  //若都没有，则说明所查询区间包含此区间的一半，就查询l到此区间一半，此区间一半到r的max
}
int main()
{
    int n,m;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        int i,x,y;
        for(i=1; i<=n; i++)
            scanf("%d",&a[i]);
        build(1,n,1);  //建树
        char c;
        while(m--)
        {
            getchar();
            scanf("%c%d%d",&c,&x,&y);
            if(c=='Q')
                printf("%d\n",query(x,y,1));  //查询区间结果
            else
                update(x,y,1); //更新区间
        }
    }
}